基于SNOP的主动配电网多时间尺度优化策略

晏阳，廖清芬，胡静竹，岑炳成，朱振山

(武汉大学电气工程学院，武汉市 430072)

基于SNOP的主动配电网多时间尺度优化策略

晏阳，廖清芬，胡静竹，岑炳成，朱振山

(武汉大学电气工程学院，武汉市 430072)

针对主动配电网(active distribution network, ADN)中分布式电源和负荷随机波动的特点，提出了基于软常开开关(soft normally open point， SNOP)的主动配电系统多时间尺度控制策略。考虑SNOP的运行工作特性，提出了在长时间尺度上通过配电网全局优化策略实现对SNOP输出进行控制，在短时间尺度上通过引入电压波动迟滞控制实现对SNOP输出参考值的动态调整，以维持线路电压平稳，提升分布式电源的消纳能力。在改进的IEEE 33节点系统中，进行了长时间尺度全局优化、短时间尺度动态调整分析，并对SNOP的安装位置、容量和数量进行了讨论。结果表明，基于SNOP的主动配电系统多时间尺度优化策略是有效可行的，且统一潮流控制器(unified power flow controller, UPFC)型SNOP较背靠背(back to back，B2B)型有更小的容量需求。

主动配电网(ADN)；随机波动；软常开开关(SNOP)；多时间尺度；动态调整；迟滞控制

0 引 言

未来配电网将发展为兼容多种发电方式和新技术，支持可再生能源发电、电动汽车充放电及其他储能装置的灵活接入和退出，实现需求响应资源的优化管理和控制的配电系统[1-2]。多电压等级、多层次环状网络将很可能成为未来配电网的主要网络结构[1]，配电网的规划、管理和运行模式等方面将发生重大变化，形成全新的运行模式[2-3]。

大量不可控分布式电源接入配电网后，会带来峰值电流增大、电压波动大和馈线负载率不均等问题[4]；此外，由于负荷种类的多样化，不同馈线的负荷水平在1天内将呈现不同的趋势，这种分布式电源和负荷的波动特性，使得同一线路在某些时刻过载而某些时刻负荷过轻。仅靠网络拓扑结构的改善，难以消纳大量分布式电源，需增加配电网络的可控设备和资源[5]，以实现网络的优化运行。

软常开开关(soft normally open point， SNOP)能够准确控制其所连两侧馈线传输的有功和无功功率[6]，参与配电网主动控制，以提高新能源消纳能力，实现配电网运行优化。同时，SNOP的引入将改变传统配电网闭环设计、开环运行的方式[7]，避免联络开关换位造成的安全隐患，使得配电网拓扑更加灵活。文献[8]分别建立了以输出有功和视在功率最小为目标的统一潮流控制器(unified power flow controller, UPFC)优化控制策略，仅对一个时间断面的优化效果进行了分析；文献[9]对背靠背电压源型SNOP的控制方式及其对配电网多时间断面的潮流优化作用进行了分析。上述研究主要集中于SNOP在时间断面上的潮流优化，而根据潮流优化策略得到的SNOP输出参考值滞后于DG和负荷的变化，不能实现实时优化。

为此，本文提出基于SNOP迟滞控制的多时间尺度配电网络优化策略。首先，分析背靠背型和统一潮流控制器型SNOP的控制模式和运行特性；其次，提出基于SNOP的多时间尺度优化策略，引入实时电压滞环控制弥补全局优化策略存在调度周期的缺陷；最后，分析多时间尺度优化策略的优化效果，验证上述策略的有效性和可行性。

1 SNOP的工作原理

馈线I上任意节点满足如下平衡：

Pi=Pi-1-PLoss(i-1,i)-PLD,i

(1)

Qi=Qi-1-QLoss(i-1,i)-QLD,i

(2)

(3)

接入SNOP后满足边界条件：

(4)

(5)

图1 SNOP接入示意图Fig.1 Schematic diagram of SNOP access

1.1 背靠背电压源模型

B2B VSC由2个电压源型逆变器组成，中间通过直流母线电容连接，如图1(b)所示。正常运行时，其中一个逆变器控制直流电压和本侧交流电压(UdcUac/UdcQ控制)，另一个控制本侧输出有功和无功功率(PQ/UacQ控制)，2个逆变器均能实现四象限内的有功、无功功率调节，B2B VSC型SNOP的对外传输功率为：

(6)

(7)

SNOP的传输损耗只占其传输功率的5%左右[6]，忽略不计，SNOP的输出应满足有功功率平衡、电压约束、VSC输出容量限制：

(8)

(9)

1.2 统一潮流控制器模型

不同于B2B VSC，UPFC的一个串联侧逆变器经变压器串联在交流线路中，另一个并联逆变器通过变压器并联到线路中，2个逆变器通过直流母线电容相连[10]，如图1(c)。其串联侧VSC通过调节注入电压的幅值Us和相角ρ灵活调节线路传输的有功和无功，而并联侧VSC为串联部分提供有功功率支撑，UPFC也可以在4个象限内灵活运行。

(11)

(12)

(13)

(14)

Us=rUiejρ

(15)

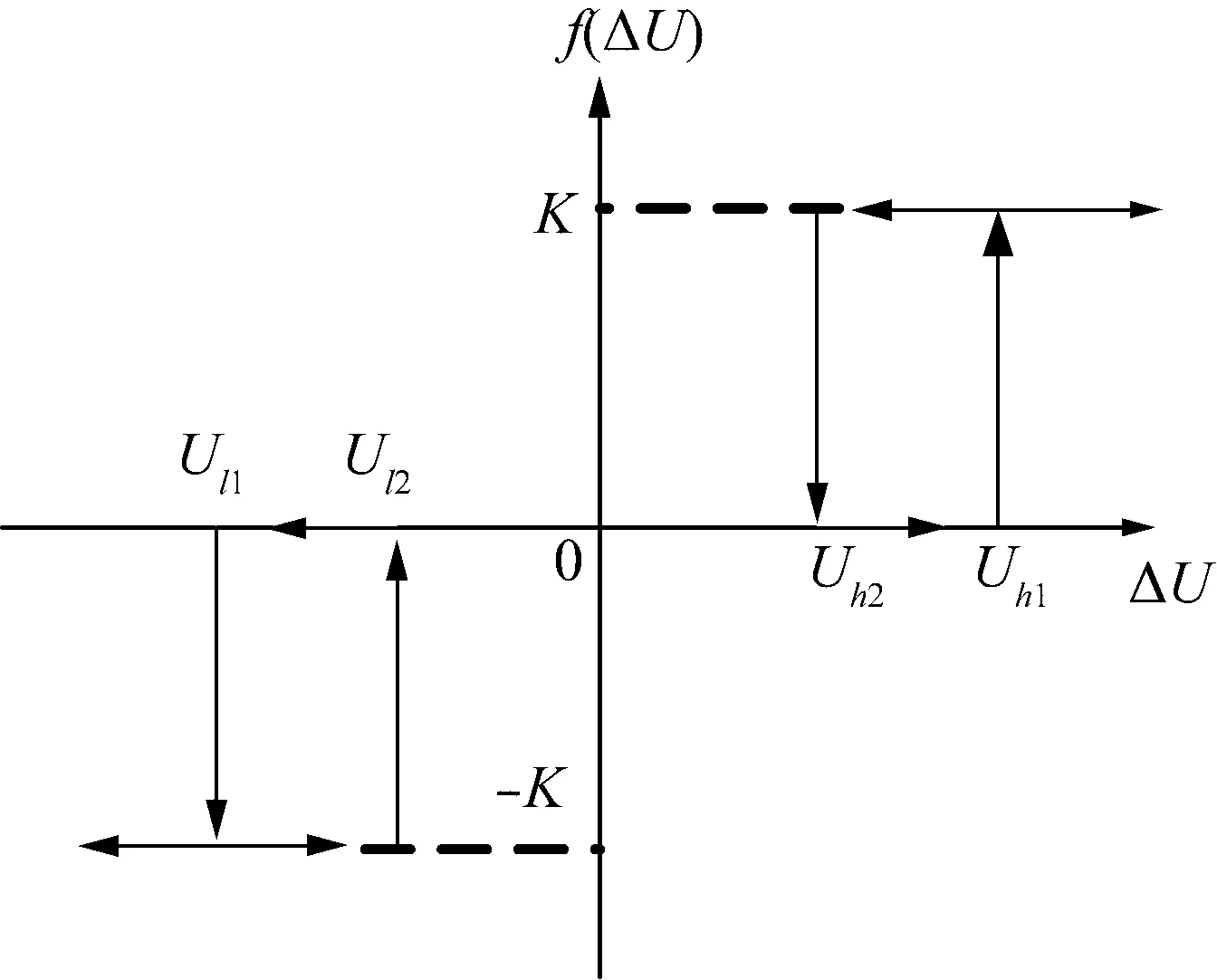
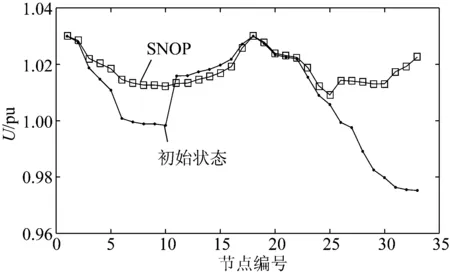
式中：θij为SNOP两输出端的电压相角差；Xs为串联侧逆变器的等效电抗。注入的串联电压Us由式(15)决定；r为UPFC的调节半径，有0

UPFC调节满足的功率平衡方程、端电压约束、并联VSC的容量限制和B2BVSC类似，特别地，其串联VSC的容量限制为

(16)

2 基于SNOP的主动配电系统运行控制优化

对主动配电系统的运行控制，是一个全局优化管理和局部动态调整相结合的过程[11]。对系统进行全局优化时，是控制中心以下一调度周期的负荷预测[12]、DG出力预测和网络信息为基础，根据最优潮流算法，分析得到各可控资源的最优调度策略，并发出控制指令。由于信息量大、信息采集周期不等、算法速度和精度限制，全局优化策略适用在长时间尺度上进行[13]。针对DG和负荷需求的实时波动，会对全局优化策略的决策带来干扰，各可控资源需根据自身的控制模式和局部量测信息，进行一定幅度的短时动态调整，以修正负荷预测和DG出力预测造成的偏差。

2.1 长时间尺度全局优化模型

对接入DG、SNOPs的配电网进行动态潮流优化，以T时段内的总网络损耗和电压偏移量最小为优化指标。

(1)网络损耗

(17)

式中：T为总时间集；i为时段编号；n为总支路数；j为支路编号。

(2)最大平均电压偏差

h2=max(mi%)，i=1，…，T

(18)

(3)综合评估指标

将上述2个指标进行归一化后利用权重系数将其合成单一综合指标：

(19)

式中：H1、H2分别为初始运行条件下h1、h2的值，ω1、ω2分别代表运行损耗和电压偏差2个指标的权重。实际配电网运行中，可根据调度运行的需求取值，本文取ω1=ω2=0.5。

上述目标综合考虑了配电网的运行成本和用户对电能质量的需求，同时，分布式电源出力采用最大功率跟踪模式，实现主动配电系统的可再生资源利用最大化。

(4)约束条件

优化模型的约束条件包括系统潮流约束、运行电压水平约束、支路电流限制约束：

Pi=PDGi+PSNOPi-PLDi

(20)

Qi=QDGi+QSNOPi-QLDi

(21)

Uimin≤Ui≤Uimax

(22)

(23)

对于SNOP，则应满足式(8)—(10)的运行边界约束。

长时间尺度优化的决策变量为SNOP两端的输出有功、无功功率，根据SNOP实际控制模式的不同，优化模型给SNOP的参考值有所区别。以B2BVSC为例，VSC1采用PQ控制时，优化模型的决策值PQ即为VSC的输出功率参考值Pref、Qref，VSC1采用PUac控制模式时，则将决策结果中VSC1电压作为其电压参考值，即Pref、Uref。这2种控制模式，均能实现长时间尺度的优化，但其适应功率波动的能力存在差别，这一点将在3.1节中进行论述。

2.2 短时间尺度控制策略

长时间尺度优化策略得到的VSC决策量难以实现实时最优，本节提出基于电压波动的短时控制策略，根据实时运行情况对VSC的参考功率进行动态修正。

在SNOP的短时控制策略中加入电压波动滞环控制模块，用以屏蔽微小的扰动信号，避免控制器频繁动作，如图2所示。图中Uh1和Uh2分别为电压波动偏差控制器的电压波动上限值和电压波动恢复值；K为电压波动比例系数。

图2 电压波动迟滞系数Fig.2 Voltage fluctuation hysteresis coefficient

长时间尺度优化除给出调度周期SNOP的参考量外，同时给出短时尺度控制需维持的观测点的电压参考量U1ref。对各测量点电压进行比较，筛选出电压与基准值偏差最大者作为观测点电压U1。在一个调度周期内，当DG和负荷功率波动而引起观测点电压波动超过阈值h1时，电压滞环控制环节作用，控制器发出调整信号，叠加在全局优化目标功率调节量上，以维持线路电压平稳。当电压波动降低到h2以下时，不再输出调整信号。基于SNOP的主动配电网(active distribution network, ADN)多时间尺度优化控制框架如图3所示。

图3 多时间尺度优化策略框架Fig.3 Multi time scale optimization strategyFrame

2.3 模型求解

本文采用生物地理学优化(Biogeography-based optimization, BBO)算法进行全局优化模型的求解，BBO优化求解的适应度指标为综合评估指标OPF，适应指数变量为SNOP的输出有功、无功，并采用余弦迁移模型和基于柯西分布的变异算子对其进行改善[14]。基于改进生物地理学优化(improved Biogeography-based optimization, IBBO)算法的全局优化求解步骤如图4所示。

图4 全局优化求解步骤Fig.4 Global optimization solving process

3 算例分析

未来配电网将很可能采用多层次环状网络结构，对于某一电压等级配电网，则会形成双端、多端供电和网状拓扑。对IEEE 33节点配电系统[15]进行改进，将节点18经变压器与主网连接，节点10-11之间增加联络开关TS6，联络开关全部断开，改进后的33节点系统如图5所示。

图5 改进的33节点配电系统Fig.5 Modified IEEE33 bus system

节点11、22、25、33接入500 kW光伏发电，节点9、28接入500 kW风电，DG的功率因数随机设置为0.9(超前)到0.9(滞后)，DG不主动参与平衡系统负荷和电压调节。该系统的日负荷预测和DG出力预测曲线如图6所示，日总运行网损为1.448 9 MW·h，最大电压偏差为-6.74%。

图6 负荷、分布式电源日预测曲线Fig.6 Daily forecasting curves of load and distributed generation

3.1 长时间尺度优化分析

3.1.1 全局优化策略效果

以在TS4处安装SNOP为例，进行全局优化，分析全局优化策略的效果。得到优化后日运行网损为0.711 7 MW·h，最大电压偏差为-2.44%，此时各节点不同时刻的电压曲线如图7所示。

图7 优化前后电压曲面Fig.7 Voltage surfaces before and after optimization

取调度时段t=21进行分析，此时各节点电压的情况与优化前对比如图8所示，SNOP两端输出功率分别为0.602 2 MVA、0.897 9 MVA，未优化时网络损耗为0.116 MW，优化后的网络损耗为0.059 MW，极大程度地改善了运行网损。初始状态下电压较低点集中在支路29-33、6-10，SNOP作用后这2条支路的电压提升明显，整个网络电压分布情况得到了显著改善。

图8 各节点电压分布Fig.8 Voltage distribution of each bus

3.1.2 SNOP位置的影响

为了比较SNOP在不同位置时全局优化的效果，在各TS处安装SNOP1—SNOP6，计算其优化效果和SNOP最小需求容量，结果见表1。

表1 SNOP安装位置结果比较

Table 1 Comparison of SNOP installation positions

结果表明，分别在TS1—TS6处单独安装SNOP均能减少系统网损和改善线路电压水平，安装位置不同，SNOP的改善作用不同，其容量需求也不同。以B2B VSC为例分析，在TS3处安装SNOP时，SNOP需求容量最小，同时运行目标改善效果最小，TS1处安装SNOP时需求容量最大，而其对优化目标的改善比TS4处要小。因此需要根据实际网络运行情况选择适当的SNOP安装位置，在合理容量的SNOP下实现配电网网络的优化运行。在本算例中，TS4处的SNOP容量需求较为合理，同时优化目标改善效果最好，安装单台SNOP时应选在TS4处。

另外由表1可知，B2B VSC和UPFC型SNOP均能实现全局最优目标，而其容量需求是不同的。相对于B2B VSC型，UPFC型SNOP并联侧逆变器容量需求较大而串联侧逆变器容量需求则显著减小，UPFC具有一定的容量优势，但其带来了需要安装串联变压器的问题，实际应用中应综合考虑2种类型SNOP的成本效益进行选择。

3.1.3 SNOP安装数量的影响

在不同位置同时安装SNOP，分析多台SNOP的联合优化效果，仿真结果见表2。

表2 多SNOP优化效果比较

Table 2 Comparison of multi SNOP optimization

可以看出，多个SNOP作用下，网损和电压水平改善程度进一步提升，但提升效果有限。随着SNOP数量的增加，新接入的SNOP优化效果却逐步下降。因此需根据成本效益分析SNOP的具体安装数量和位置，下文仅针对单台SNOP时的短时控制策略进行讨论。

3.2 短时动态调整

研究表明，光伏发电功率瞬时波动不超过其最大输出功率的一半[16]，而负荷的瞬时波动性较小。考虑最极端的情况，在短时间尺度自适应控制中，模拟DG功率100%随机波动，同时负荷功率保持不变，如图6所示。UPFC型SNOP安装在TS4处，长时间尺度优化策略下t=16：00时的SNOP参考值见表3，线路26—33为电压观测点。设定观测点电压基准值为1.010，电压波动调整阈值和回落值分别取±0.004和±0.002。在Digsilent中进行短时动态仿真，分析本文提出的短时控制策略的有效性，不同VSC控制模式下，节点29电压波动情况见图9。

表3 全局优化参考值

Table 3 Global optimization reference value

图9 节点电压波动情况Fig.9 Voltage fluctuations of bus

可以看出，当VSC采用PQ(UdcQ)控制时，SNOP向两侧输出的功率能够维持在Pref、Qref，不具备动态调整线路电压的能力。当VSC采用PUac(UdcUac)控制时，SNOP能够调节输出无功，维持传输的有功功率和两侧电压幅值恒定，因而同一线路上观测点的电压波动范围也适当减小。

当引入电压滞环控制进行动态调整后，PQ控制模式下，节点29的电压在多个时刻超出了电压波动阈值h1，滞环控制环节输出调节信号，对SNOP的无功功率参考值进行修正，直至SNOP的电压波动回落到h2以下，控制电压在微小范围内波动。采用PUac控制时，滞环控制环节输出调节信号，对SNOP的端电压参考值进行修正，使得VSC不再只维持该输出点的电压恒定，同时兼顾了维持多观测点电压的能力，线路的电压波动情况得到明显改善。值得注意的是，PUac控制时，短时间尺度控制策略的动作次数少于PQ控制的情况，其配合短时间尺度控制策略后整体的电压波动幅度更小，线路电压分布更佳。

需要指出，当全局优化调度周期足够短即能够实时更新SNOP输出参考量时，线路电压波动同样可以得到明显改善，如图9所示。但是实际运行过程中，全局优化的调度周期需依托于电网中的信息采集和监控系统、通信系统以及算法的速度，因而需要配合短时就地控制策略进行多时间尺度的优化。上述仿真结果表明，本文所提基于SNOP的主动配电网多时间尺度优化控制策略是合理可行的。

4 结 论

(1)基于SNOP的多时间尺度优化策略是有效可行的，在长时间尺度上通过控制SNOP的输出可实现全局优化，在短时间尺度上引入电压滞环控制可减小分布式电源功率和负荷波动引起的电压波动。

(2)长时间尺度优化效果与SNOP的位置、数量有关，且UPFC相较B2B型SNOP最小容量需求更小。

(3)SNOP的短时动态调整效果与其控制模式有关，PV控制模式下能够更好地维持电网平稳，从而提升未来配电系统对分布式电源的消纳能力。

实际配电系统中采集的数据是局部的、间断的，根据局部量测信息制定优化策略，是下一步的研究方向。

[1]马钊,周孝信,尚宇炜,等. 未来配电系统形态及发展趋势[J]. 中国电机工程学报, 2015, 35(6): 1289-1298.MAZhao,ZHOUXiaoxin,SHANGYuwei,etal.Formanddevelopmenttrendoffuturedistributionsystem[J].ProceedingsoftheCSEE, 2015, 35(6): 1289-1298.

[2]GANCK,PUDJIANTOD,DJAPICP,etal.Strategicassessmentofalternativedesignoptionsformultivoltage-leveldistributionnetworks[J].IEEETransactionsonPowerSystems，2014，29(3)：1261-1269.

[3]范明天,张祖平,苏傲雪,等. 主动配电系统可行技术的研究[J]. 中国电机工程学报, 2013, 33(22): 5, 12-18.FANMingtian,ZHANGZuping,SUAoxue,etal.Enablingtechnologiesforactivedistributionsystems[J].ProceedingsoftheCSEE, 2013, 33(22): 5, 12-18.

[4]王成山,孙充勃,李鹏. 主动配电网优化技术研究现状及展望[J]. 电力建设, 2015, 36(1): 8-15.WANGChengshan，SUNChongbo，LIPeng.Reviewandperspectiveontheoptimizationofactivedistributionnetwork[J].ElectricPowerConstruction, 2015, 36(1):8-15.

[5]王守相,葛磊蛟. 主动配电系统运行与控制关键技术[J]. 电力建设, 2015, 36(1): 85-90.WANGShouxiang，GELeijiao.Keytechnologyofoperationandcontrolofactivedistributionsystem[J].ElectricPowerConstruction, 2015, 36(1): 85-90.

[6]BLOEMINKJM,GREENTC.Increasingdistributedgenerationpenetrationusingsoftnormally-openpoints[C]//2010IEEEPowerandEnergySocietyGeneralMeeting,Minneapolis,MN,USA,2010: 1-8.

[7]王岸.SNOP的研究及其在配电网中的应用[D]. 北京: 北京交通大学, 2015.WANGAn.ResearchonSNOPanditsapplicationindistributionnetwork[D].Beijing:BeijingJiaotongUniversity,2015.

[8]仉志华,徐丙垠,陈青. 基于统一潮流控制器的配电环网潮流优化控制策略[J]. 电网技术, 2012, 36(6): 122-126.ZHANGZhihua,XUBingyin,CHENQing.ControlstrategiesforUPFC-basedoptimalpowerflowofdistributionnetworkwithnormallyclosed-loopoperation[J].PowerSystemTechnology, 2012, 36(6): 122-126.

[9]王成山,孙充勃,李鹏,等. 基于SNOP的配电网运行优化及分析[J]. 电力系统自动化, 2015, 39(9): 82-87.

WANGChengshan,SUNChongbo,LIPeng,etal.SNOP-basedoperationoptimizationananalysisofdistributionnetworks[J].AutomationofElectricPowerSystem, 2015, 39(9): 82-87.

[10]武智慧. 考虑统一潮流控制器的电力系统优化潮流研究[D].沈阳：沈阳工业大学，2013.WUZhihui.Researchonpowersystemoptimalpowerflowwithconsideringunifiedpowerflowcontroller[D].Shenyang：ShenyangUniversityofTechnology，2013

[11]尤毅,刘东,钟清,等. 多时间尺度下基于主动配电网的分布式电源协调控制[J]. 电力系统自动化, 2014, 38(9): 192-198, 203.YOUYi,LIUDong,ZHONGQing,etal.Multi-timescalecoordinatedcontrolofdistributedgeneratorsbasedonactivedistributionnetwork[J].AutomationofElectricPowerSystem,2014, 38(9): 192-198, 203.

[12]钟清,孙闻,余南华,等. 主动配电网规划中的负荷预测与发电预测[J]. 中国电机工程学报, 2014, 34(19): 3050-3056.ZHONGQing,SUNWen,YUNanhua,etal.Loadandpowerforecastinginactivedistributionnetworkplanning[J].ProceedingsoftheCSEE, 2014, 34(19): 3050-3056.

[13]高亚静,李瑞环,梁海峰,等. 考虑间歇性电源与负荷不确定性情况下基于多场景技术的主动配电系统两步优化调度[J]. 中国电机工程学报, 2015, 35(7): 1657-1665.GAOYajing,LIRuihuan,LIANGHaifeng,etal.Twostepoptimaldispatchbasedonmultiplescenariostechniqueconsideringuncertaintiesofintermittentdistributedgenerationsandloadsintheactivedistributionsystem[J].ProceedingsoftheCSEE, 2015, 35(7): 1657-1665.

[14]曾鸣,韩旭,李博. 考虑不确定性的多阶段主动配电网规划模型研究[J]. 电力建设, 2015, 36(1): 65-71.ZENGMing，HANXu，LIBo.Studyofmultistageplanningforactivedistributionnetworksunderuncertainty[J].ElectricPowerConstruction, 2015, 36(1):65-71.

[15]BaranME，WuFF.Optimalcapacitorplacementonradialdistributionsystems[J].IEEETransactionsonPowerDelivery，1989,4(1):725-734.

[16]黄炜,刘健,魏昊焜,等. 分布式光伏电源极端可接入容量极限研究[J]. 电力系统保护与控制, 2015, 43(3)：22-28.HUANGWei,LIUJian,WEIHaokun,etal.Extremecapacitylimitationsofphotovoltaicgeneratorsindistributiongrids[J].PowerSystemProtectionandControl, 2015, 43(3): 22-28.

(编辑 张媛媛)

Multi-Time Scale Optimization Strategy of Active Distribution Network Based on SNOP

YAN Yang, LIAO Qingfen, HU Jingzhu, CEN Bingcheng, ZHU Zhenshan

(School of Electrical Engineering, Wuhan University,Wuhan 430072, China)

According to the stochastic volatility characteristics of distributed generation and load in active distribution network, this paper proposes the multi-time scale optimization strategy for active distribution network based on soft normally open point (SNOP). With considering the operating characteristics of SNOP, we control the output power of SNOP through the global optimization strategy of distribution network on long-time scale, and realize the dynamic adjustment on the output reference value of SNOP through voltage fluctuation hysteresis control on short-time scale, which can maintain the line voltage stable, and enhance the absorptive capacity of the distributed generation. In the improved IEEE-33 bus system, we analyze the global optimization on long-time scale and the dynamic adjustment on short-time scale, as well as discuss the installation position, capacity and number of SNOP. The results show that the multi-time scale optimization strategy of active distribution network based on SNOP is feasible and effective, and UPFC-type SNOP has a smaller capacity requirement than that of B2B-type.

active distribution network(ADN); stochastic volatility; soft normally open point (SNOP); multi-time scale; dynamic adjustment; hysteresis control

国家电网公司科技项目(5211011400BT)

TM 712

A

1000-7229(2016)02-0125-07

10.3969/j.issn.1000-7229.2016.02.018

2015-09-15

晏阳(1991)，男，硕士，研究方向为主动配电网、电力系统运行分析与控制；

廖清芬(1975)，女，副教授，硕士生导师，研究方向为电力系统分析与运行；

胡静竹(1990)，女，硕士，研究方向为电力系统运行分析与电磁兼容;

岑炳成(1990)，男，硕士，研究方向为电力系统运行与控制;

朱振山(1989)，男，博士，研究方向为电力系统运行与控制。