电力系统多时间尺度灵活性指标研究

2016-02-16王鹏李宏仲吕风磊孙伟卿邱文平吴俊玲

电力建设 2016年2期

王鹏，李宏仲，吕风磊，孙伟卿，邱文平，吴俊玲

(1.上海电力学院电气工程学院，上海市 200090；2.国网山东省电力公司东营供电公司，山东省东营市 257091； 3.上海理工大学光电信息与计算机工程学院，上海市 200093;4.国网福建省电力有限公司南平供电公司，福建省南平市 353000；5. 中国电力科学研究院，北京市 100192)

电力系统多时间尺度灵活性指标研究

王鹏1，李宏仲1，吕风磊2，孙伟卿3，邱文平4，吴俊玲5

为了更好地解决间歇性电源接入电网的问题，应对风电的不确定性，考虑负荷的变化，提出了电力系统多时间尺度的灵活性评价模型。首先对风电的不确定性进行了介绍，阐述了灵活性的概念和特点，从应对电网中风电场出力变化能力的角度，针对负荷的变化，列举了3类不同的时间尺度，提出了基于不同时间尺度下系统响应电网中风电场出力变化最大速率的灵活性评价模型；对具体的灵活性评价数学模型进行阐述，并利用内点法实现了模型的求解。最后，以甘肃电网为例，对文中提出的灵活性指标进行了具体的算例说明。

电力系统灵活性；风电不确定性；多时间尺度；评价指标

0 引言

在风电等间歇性电源[1]接入电网前，电力系统的不确定性主要来自于负荷的变化、电网故障以及常规电源故障引起的意外扰动。大规模风电接入电网带来的挑战主要是给电力系统注入了更大的波动性和不确定性。因此，电力系统需要更多的灵活性资源来应对来自电源侧、负荷侧以及电网侧的不确定性。而应对这些挑战的核心在于通过改进相关的技术、方法和措施，提高电力系统的灵活性，从而确保电力系统能够随时维持发电与负荷的平衡，保证电力系统的可靠性和安全性。

各国学者针对不同的应用领域，提出相应的电力系统灵活性评价指标。文献[2]将基于功率谱密度的风电变化情况和灵活性资源进行对比，得到了灵活性价值评估。文献[3]以电力系统容量、能量存储容量、容量斜坡率和容量持续时间为基本参数，以单节点的潮流为出发点，针对电力系统运行的灵活性建立了评估模型。文献[4-5]分别对基于IRRE指标因变量和TUSFI-TEUSFI指标的2种灵活性评估方法进行了详细的介绍。

已有的灵活性评价指标均仅认为电力系统灵活性的自变量存在于输电系统，并以容量、潮流或等价的成本为参数，构建灵活性评价指标。但未能全面考虑负荷变化对系统灵活性的影响，没有考虑负荷变化的特点与时间特性对电力系统灵活性的影响程度[6-8]。本文在上述背景下，针对风电的不确定性，依据电力系统灵活性的定义，考虑负荷变化情况，对不同时间尺度下电力系统对风电的功率接纳度进行评估，提出电力系统多时间尺度灵活性评价指标，体现了电力系统解决风电不确定性的量化思路。

1 多时间尺度灵活性评价模型

电力系统灵活性概念由北美电力可靠性委员会(NERC)和国际能源署(IEA)针对电力系统灵活性给出了较为完整的定义。NERC认为，电力系统灵活性是利用系统资源满足负荷变化的能力，主要体现于运行灵活性[9]；IEA则认为，电力系统在其边界约束下，快速响应供应和负荷的大幅波动，对可预见不可预见的变化和事件迅速反应，负荷需求减小时减小供应，负荷需求增加时增加供应[10]。上述定义都未能考虑多时间尺度下的灵活性需求，对于电力系统灵活性，通常认为其有3个特点：灵活性是电力系统的固有特征；灵活性具有方向性；灵活性需在一定时间尺度下描述。

考虑灵活性概念，本文将一定时间内响应风电变化的能力称为灵活性，即一定时间尺度下电力系统中所有灵活调节电源和储能设备能够承受的风力发电功率最大突变速率称为电力系统灵活性。该指标分为向上灵活性和向下灵活性两大类，分别对应风电功率突降和突增。

考虑负荷的波动性，以上电力系统灵活性评估需在不同时间尺度下进行，以便调用不同的灵活性资源。在本文中，时间尺度tscale的选择主要依据国标对风电场接入电力系统的技术规定进行，分别选择24 h，1 h，10 min和1 min。

1.1 1 min和10 min时间尺度模型

在1 min和10 min时间尺度下，认为负荷保持不变，即在正常运行方式下，系统应该满足风电场在这一限制范围内功率波动，即将上述规定作为1 min和10 min时间尺度的风电功率波动所引起的灵活性需求的限值，短时间尺度的灵活性主要体现了系统当前状态下承受风电的波动能力，能够为新增快速储能装置提供量化支撑。

根据灵活性定义[11-13]，具体而言，从应对电网中风电场出力变化能力的角度，以系统响应电网中风电场出力变化的最大值的变化率作为衡量系统当前状态下系统灵活性的量化指标。

为了更加丰富地体现系统的灵活性，根据控制手段和对象的不同，可以将电力系统灵活性评估的功率评价指标细化为如表1所示的形式。其中，控制手段既包含单一的控制手段，如调整传统机组出力、储能设备等，也包含各种控制手段的组合；控制对象既包含整个电网内风电场出力的变化，也包含某些区域内风电场出力的变化。

表1 灵活性评估

Table 1 Flexibility assessment

则形成相应的评价矩阵如下：

(1)

式中：FPi,j表示以第i种控制手段对第j种控制对象进行控制时，系统对风电场功率变化的短时调节能力，即灵活性。

综上所述，利用灵活性评价指标可以对电力系统电源的灵活性进行评估，根据相应灵活性资源的调节能力来应对风电的不确定性，从而量化资源的灵活性调节能力，为保证电网的安全稳定运行提供合理的建议。

1.2 1 h时间尺度模型

在1 h时间尺度模型下，负荷会出现明显的变化，为了体现负荷的变化以及评估该时间尺度下的灵活性能力，可以将1 h内的负荷曲线变化归纳为以下4种类型：

(1)单调递增型，如图1(a)；

(2)单调递减型，如图1(b)；

(3)凹函数V型，如图1(c)；

(4)凸函数倒V型，如图1(d)。

图1 负荷-时间曲线Fig.1 Load-time curve

对每一类型的曲线分割成6段曲线，每一段按10 min的方法求取向上和向下的灵活性，将得到的数据拟合成2条浮动曲线，如图2所示，2条虚线分别代表着系统向上和向下的功率变化情况，曲线的斜率则为该时间尺度下的灵活性能力。

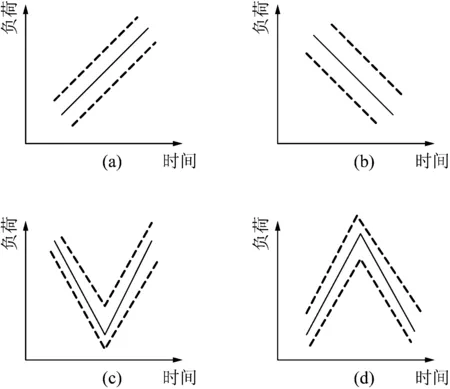
图2 负荷-时间浮动曲线Fig.2 Load-time floating curve

1 h时间尺度的灵活性指标能够间接体现1 h内的风电变化率，能够为更有效地调用灵活性资源提供参考。

1.3 24 h时间尺度模型

风电在24 h时间尺度上的灵活性需求主要表现为风电日出力曲线的反调峰特性引起的调峰容量需求。

因此，如图3所示，利用电力系统最大运行方式下的数据，按照最大负荷情况确定系统开机后，进行最小负荷情况下长时间尺度的向上灵活性计算，然后将这一数值作为衡量反调峰的容量需求。

图3 24 h负荷-时间曲线Fig.3 24 h load-time curve

风电不可控的波动性是其对电力系统调度运行的主要影响因素之一，将会对系统调度运行产生重大影响，系统拥有足够灵活的可调节容量是系统接纳风电的先决条件之一，所以使用灵活性指标作为衡量反调峰的容量需求，具有重要的实践意义。

综上所述，在不同时间尺度下，将风电场的可接纳风电(系统可提供)的最大波动/时间(速率)作为电力系统的灵活性指标，这样能够为是否增加储能等资源(灵活性需求)提供参考，并对电网的接纳和承受潜力进行评估。表2的曲线是3种时间尺度下的灵活性指标的结果输出，其中，ΔP/tscale为每一时间尺度下对应的灵活性数值。如果系统当前运行方式下灵活性评估的结果小于风电要求值，就说明系统能够提供的灵活调节能力不能满足风电功率波动的灵活性需求。反之，如果评估结果大于这一限值，则表明系统能够满足来自风电的灵活性需求。

表2 灵活性评估汇总

Table 2 Flexibility assessment

2 多时间尺度灵活性评价模型求解

多时间尺度灵活性评价模型求解是一个基于潮流等式方程和电压、相角等不等式约束的最优化问题。本文采用原对偶内点法进行数值求解。

2.1 目标函数

(2)

式中：ΔPwi表示研究区域内风电场i的出力变化，且以风电场功率向下的变化为正，ΔPwi应不小于0；Nw表示研究区域内风电场的个数；tscale表示时间尺度。

目标函数的值越大，说明电力系统的应对能力越强，电力系统的灵活性则越佳。

2.2 约束条件

为了便于描述，将约束条件分为2类：第1类约束条件为通用约束，通用约束的形式与传统电力系统约束相似，也是灵活性指标计算中必须考虑的约束；第2类约束条件为灵活性资源约束，反应了对不同类型灵活性资源的特殊要求。

由于目标函数的影响，节点功率平衡方程应分别考虑风电场节点和非风电场节点。

对于风电场节点，功率平衡方程为

(3)

式中：PGk、QGk分别为节点k的有功功率和无功功率；PLk、QLk分别为节点k的有功负荷和无功负荷；ΔPwk、ΔQwk分别为节点k的风电有功变化和无功变化；Uk为节点k的电压；Gkj、Bkj、θkj分别为节点k和j之间的电导、电纳和相角差。

电压约束：

(4)

线路约束：

(5)

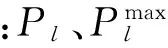
现以火电机组为例，其他类型同理。系统中每一台非满载的火电机组都能够提供向上和向下的灵活性。灵活性的时间尺度将影响火电机组的有功出力范围，因此，综合传统的上下限出力约束以及灵活性时间尺度与机组爬坡速率约束，火电机组的有功出力约束可写成如下形式：

max{PTG,min,PTG,0-rTd·Δt}≤PTG≤

min{PTG,max,PTG,0+rTu·Δt}

(6)

式中：PTG表示火电机组的出力；PTG,0、PTG,max、PTG,min分别表示火电机组的当前出力以及其出力的上、下限；rTu、rTd分别表示火电机组的向上和向下的爬坡速率。

2.3 指标模型求解

内点法是目前用求解非线性规划问题最常用的方法。特别是对于约束条件和变量数目较多的大规模线性规划问题，内点法收敛特性和计算速度均优于单纯形法。故对于上述建立的优化数学模型，本项目采用内点法进行求解。

本文采取原对偶内点法[14-15]，求解模型(7)的最优解：

(7)

式中：f(x)表示目标函数；h(x)代表功率平衡方程；g(x)表示不等式约束条件。

应用内点法求解非线性规划问题时，首先需构造如下形式的拉格朗日函数

(8)

式中：l和u为松弛向量；L为障碍参数；y，z，w为对应等式约束和不等式约束的拉格朗日乘子；r为不等式约束维数。

根据等式(8)得到KKT一阶最优条件方程组，通过牛顿法处理方程组，并利用稀疏矩阵和高斯消元法进行求解对偶变量，最后通过迭代得到满足收敛条件的最优解。基于C++对模型利用原对偶内点法求解具体过程如图4。

3 算例分析

为了验证评价模型的实用性，下面结合甘肃算例系统，计算系统不同时间尺度的灵活性指标，并对指标的实际意义进行说明。

算例系统有145台发电机，总装机容量为37 247 MW，其中火电机组共33台机组，装机容量为14 270 MW；供热机组共16台，容量为6 060 MW；水电机组共23台，容量为2 733 MW；风电机组共73台，容量为14 184 MW。考虑系统备用及运行方式，令火电机组与供热机组出力上限为其装机容量的95%，出力下限分别为50%与70%，水电机组出力上限为其装机容量的100%，出力下限为0。其中火电与供热机组爬坡速度按每min装机容量的2%考虑，水电机组爬坡速率按照每min容量的50%考虑。最大有功负荷共计22 517.9 MW，最小负荷共计18 014.3 MW。系统发电机组出力总体情况如表3所示。

图4 内点法的流程图Fig.4 Flowchart of interior point method表3 系统机组出力情况Table 3 Output of power unit

考虑到系统中各类型机组的爬坡能力与其出力限制，此处不将各个机组出力一一列出，仅将各类型机组功率波动限值给出，如表4所示。其中机组爬坡能力表示该时间尺度下机组所能爬坡的功率极限，机组出力限值表示机组的出力极限与初始出力之差。

结合表2，丰富不同时间尺度下的计算场景，利用内点法计算的灵活性指标如表5所示。

由该结果与之前对系统其他机组出力的限制与爬坡能力的统计，可知系统1 min向上灵活性主要受到火电热电机组爬坡能力的限制以及水电机组出力极限的限制。1 min活性主要受到机组爬坡能力的约束，个别情况下热电机组则受到其出力下限的约束。而10 min系统灵活性则与1 min系统灵活性所受约束相反，其火电热电机组主要受其出力限值的约束，水电机组则根据其初始出力情况受到出力上下限约束明显。结果也表明在1 min时间尺度下，最大负荷及最小负荷情况下，系统向上灵活性与向下灵活性的大小呈对称状态，即大负荷向上灵活性小于小负荷向上灵活性，大负荷向下灵活性大于小负荷向下灵活性。指标最小的2个情况均为大负荷时系统向上灵活性，其占风电装机容量之比分别为8.8%，14.3%。某风电厂12 h、15 min、1 min内出力波动最大变化(与装机容量的比值)分别为55.4%、23.7%、6.8%，则本系统满足风电在短时间尺度内波动至少90%以上的情况。所以基本可以满足系统的灵活性需求，故其调频能力不存在显著问题。1 h时间尺度的数据情况和短时间的相似，只是由于时间尺度更长，风电功率的变化率更平缓一些，因而在选择灵活性资源方面更加多样化。

表4 系统爬坡及出力情况

Table 4 Grade and output of power unit

表5 甘肃算例灵活性评估Table 5 Gansu flexibility assessment MW/min

对于24 h时间尺度的灵活性而言，按照最大负荷情况确定系统开机后，进行最小负荷情况下长时间尺度的灵活性计算，如果取24 h风电波动范围大于其装机容量的80%，即长时间灵活性需求为(7.88×24×60)MW=11 347 MW。可见系统在调峰时，将会遇到较大问题，其功率至少存在6 100 MW的差距。将导致系统在风电增加的时候无法接纳更多的风电容量。这是由于热电机组无法充当灵活调节电源，而水电装机容量与风电装机容量又存在较大差距导致的。

在上述实际算例中，简单地从灵活性电源的方向性和时间尺度上进行了综合考虑，得到了评价系统灵活性的速率指标，这样能够为大规模风电并网后，降低风电随机性和间歇性给系统的调峰调频带来的负面影响，提供一定的建议和思路。如果系统当前运行方式下灵活性评估的结果小于风电要求值，就说明系统能够提供的灵活调节能力不能满足风电功率波动的灵活性需求。反之，如果评估结果大于这一限值，则表明系统能够满足来自风电的灵活性需求。

4 结语

为了更好地利用灵活性电源，解决风电不确定性对电网的影响，文章提出了多时间尺度的灵活性评价模型。该模型研究了不同时间尺度下的负荷特性，以及利用内点法对模型进行了灵活性数值的求解，量化了灵活性资源针对风电的调节能力，为进一步解决风电接入系统的问题提供了思路和建议。

[1]张丽英，叶廷路，辛耀中，等.大规模风电接入电网的相关问题及措施[J].中国电机工程学报，2010，30(25)：1-9. ZHANG Liying，YE Tinglu，XIN Yaozhong，et al.Problems and measures of power grid accommodating large scale wind power[J].Proceedings of the CSEE，2010，30(25)：1-9.

[2]BOUFFARD F，ORTEGA V M.The value of operational flexibility in power systems with significant wind power generation[C]//Proceedings of the Power and Energy Society General Meeting.San Diego California，USA：IEEE，2011：24-29.

[3]ULBIG A ， ANDERSSON G. On operational flexibility in power systems[C]//Proceedings of the Power and Energy Society General Meeting.San Diego California，USA：IEEE，2012：22-26.

[4]LANNOYE E，FLYNN D，O’MALLEY M.Evaluation of power system flexibility[J].IEEE Transactions on Power Systems，2012，27(2)：922-931.

[5]CAPASSO A，FALVO M C，LAMEDICA R，et al.A new methodology for power systems flexibility evaluation[C]//Proceedings of the Power Technology.Russia：IEEE，2005：27-30.

[6]肖定垚，王承民，曾平良，等.电力系统灵活性及其评价综述[J].电网技术，2014，38(3)：1569-1576. XIAO Dingyao，WANG Chengmin，ZENG Pingliang，et al.A survey on power system flexibility and its evaluations [J].Power System Technology，2014，38(3)：1569-1576.

[7]薛禹胜，雷兴，薛峰，等.关于风电不确定性对电力系统影响的评述[J].中国电机工程学报，2014，34(29)：5029-5040. XUE Yusheng，LEI Xing，XUE Feng，et al. A review on impacts of wind power uncertainties on power systems [J].Proceedings of the CSEE，2014，34(29)：5029-5040.

[8]迟永宁，刘燕华，王伟胜，等. 风电接入对电力系统的影响[J]. 电网技术，2007，31(3)：77-81. CHI Yongning，LIU Yanhua，WANG Weisheng, et al. Study on impact of wind power integration on power system[J]. Power System Technology，2007，31(3)：77-81.

[9]ADAMS J，O’MALLEY M，HANSON K.Flexibility requirements and potential metrics for variable generation：implications for system planning studies[M].Princeton，NJ：NERC，2010：14-17.

[10]Internation Energy Agency.Empowering variable renewables-options for flexible electricity systems[M].OECD Publishing，2009.

[11]张文亮，丘明，来小康.储能技术在电力系统中的应用[J].电网技术，2008，32(7)：1-9. ZHANG Wenliang，QIU Ming，LAI Xiaokang. Application of energy storage technologies in power grids[J].Power System Technology，2008，32(7)：1-9.

[12]白玉东，王承民，衣涛，等.基于柔性分析的风电并网容量优化建模[J].电力系统自动化，2012，36(12)：17-24. BAI Yudong，WANG Chengmin，YI Tao，et al.An optimization model of wind power grid-connected capacity based on flexibility analysis[J].Automation of Electric Power Systems，2012，36(12)：17-24.

[13]孙伟卿，王承民，张焰，等.采用柔性化方法表示刚性约束的电力系统优化模型[J].电网技术，2012，36(3)：120-126. SUN Weiqing，WANG Chengmin，ZHANG Yan，et al.A power system optimization model adopting flexible expression of rigid constraints[J].Power System Technology，2012，36(3)：120-126.

[14]江全元，黄志光.基于功率电流混合潮流约束的内点法最优潮流[J].电力系统自动化，2009，33(12)：32-37. JIANG Quanyuan，HUANG Zhiguang. Power-current hybrid power fow model based optimal power flow by interior point method [J].Automation of Electric Power Systems，2009，33(12)：32-37.

[15]QUINTANA V H，TORRES G，LPALOMO M.Interior-point methods and their applications to power systems：a classification of publications and software codes[J]. IEEE Transactions on Power Systems，2000，15(1)：170-175.

(编辑刘文莹)

Multi-Time Scale Flexible Indices of Power System

WANG Peng1, LI Hongzhong1, LYU Fenglei2, SUN Weiqing3, QIU Wenping4, WU Junling5

(1.College of Electrical Engineering，Shanghai University of Electric Power, Shanghai 200090, China;2. Dongying Power Supply Company, State Grid Shandong Electric Power Corporation,Dongying 257091, Shandong Province, China;3. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science & Technology, Shanghai 200093, China;4. Nanping Power Supply Bureau of State Grid Fujian Power Company, Nanping 353000, Fujian Province, China;5. China Electric Power Research Institute, Beijing 100192, China)

To solve the problem of intermittent power connected to grid, this paper proposes the flexibility evaluation model of multi-time scale power system with considering wind power uncertainty and load fluctuation. This paper firstly introduces the wind power uncertainty, and describes the concept and characteristic of flexibility. From the view of the output change capacity of the wind farm in power grid, according to the change of load, we enumerate three kinds of time scales, and propose the flexibility evaluation model for the system response to the maximum change rate of wind farm output in power grid based on different time scales. Then, we explain the mathematical model of specific flexibility evaluation, and use interior point method to solve the model. Finally, taking Gansu power system as an example, the proposed flexibility indices is illustrated by a specific example.

power system flexibility; wind power uncertainty; multi-time scale; evaluation index

国家电网公司科技项目(XT71-13-032)，国家自然科学基金项目(51407117)，上海市青年科技英才“扬帆计划”项目(14YF1410100)

TM 715

1000-7229(2016)02-0057-06

10.3969/j.issn.1000-7229.2016.02.008

2015-11-05

王鹏(1985)，男，硕士研究生，研究方向为电力系统规划；

李宏仲(1977)，男，博士，副教授，研究方向为电力系统规划；

吕风磊(1987)，男，工程师，研究方向为电力系统安全与稳定；

孙伟卿(1985)，男，博士，研究方向为电力系统经济运行；

邱文平(1987)，男，工程师，研究方向为电力系统可靠性；

吴俊玲(1978)，女，工程师，研究方向为电力系统稳定性。