拖缆水动力学的正问题与反问题研究

张大朋，朱克强，牛天鑫，王自发

（1.宁波大学海运学院，宁波315211；2.中海油天津分公司，天津300450）

拖缆水动力学的正问题与反问题研究

张大朋1，朱克强1，牛天鑫1，王自发2

（1.宁波大学海运学院，宁波315211；2.中海油天津分公司，天津300450）

基于不可压缩流体中受到水动力曳力作用下的不可伸长的挠性缆索的二维运动模型，研究了在海洋地震勘探中重构与流线型拖缆冲击的海流速度的问题。首先介绍了正问题模型，并在已知拖船运动和水动力载荷的条件下对拖缆的速度、曲率和张力进行了求解。然后，通过离散缆索形状和张力的样本值，提出了推断到海流速度的反问题，并发现这个反问题是缺秩和不适定的。在鲁棒离散噪声信号的背景下，解决逆问题数值稳定问题，采用了基于广义Tikhonov正则化算法。为了验证该方案的实用性，给出了一些用模拟噪声数据重建海流的例子。

拖缆水动力学；海流速度重组；病态反问题

对于拖曳线列阵来说，海流速度对于优缆索线型非常重要。根据海流作用在拖缆上的水动力去研究拖缆的空间几何形态及张力已经在国内外大量的文献中有详细的论述与研究［1-6］，这就是所谓的拖缆水动力学的正问题；而拖缆水动力学的反问题是通过已知的拖缆的空间几何形态及其张力去反推出拖缆周围的海流流速分布情况，这在国内学术界内相关研究资料较少。这就在逆参数辨识问题背景下提出了一个问题，即通过定位及张力测量来重现沿拖缆海流流速分布图。

本文选择了一个简单的拖缆二维运动模型，首先提出了正演模型来描述在水动力作用下缆索运动，简单讨论了几种有限差分解法。然后通过积分方程重构正演模型推导出反问题，并用广义Tikhonov正则化解决。以奇值分析和敏感性讨论为背景，概述了反问题的数值特征，还解决了阻力系数中涉及到的噪声鲁棒性和不确定性。并用仿真算例验证了该方法。计算结果表明，该方法对实际的工程实践有一定指导意义。

1拖缆正问题水动力学模型

忽略惯性项，在切向-法向的坐标系中，给出拖缆的牛顿运动定律以及动量方程

为表示缆索的形状和方向对于相应的速度分量的影响，给出缆索的运动学方程

式中：T（s，t）指在时间t时，与拖曳点距离为s处的张力；ρ为海水密度，d为缆索直径，Ct为切向阻力系数，Cn为法向阻力系数，θ（s，t）为指s上的切向量和x轴正方向之间的方位度，∂θ/∂s为缆索曲率。缆索在切向和法线方向上的相对速度分别用Vtr（s，t）和Vnr（s，t）来表示，对应的海流速度为u（s，t）和v（s，t），Vt（s，t）和Vn（s，t）分别为缆索的切向绝对速度和法向绝对速度。

抛物形方程组（1）～（4）是从笛卡尔坐标系（X，Y）以θ角通过正交变换到二维坐标系（t，n）得到的。其中，t（s）是指缆索上在s点的单位切向量，n（s）是指单位法向量。拖曳系统的构型如图1所示。

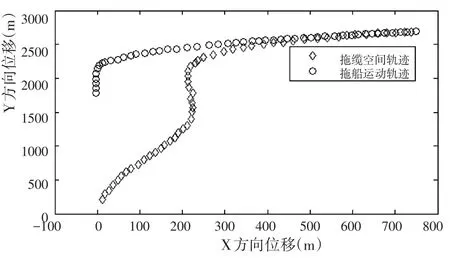
图1 二维条件下拖缆的局部及全局构型Fig.1 Local and global configuration of towed cable under two dimensional condition

如果系统在初始状态是静止的，4个边界条件完全在系统中实施。缆索铰接于拖船，缆索前端速率是

式中：θ（0，t）为缆索起始端的方位角，v1（t）和v2（t）是在时间t时船速在笛卡尔坐标系下的分量，在这里设定v1和v2的合速度v船合=2.57 m/s。注意到根据条件（6）～（7）以参数形式给出的缆索速度的边界信息，而给出缆索速率的边界信息，需要预先知道拖曳点的角度以确定该点的速度。如图1所示，在缆索和拖船铰接的部位，拖船的速度就是缆索在此点的速度，而随着缆索离铰接点位置越来越远，沿缆索长度方向某一位置的速度与拖船的速度相差越来越大。

［7-9］中考虑尾端（自由端）的张力为0，这样的话，从理论上来说，作用力和时间段的总和也会随之消失。然而，在震动缆索的尾部，通常装备有一个附在表面浮标来获取一尾部的拖曳力［10］。事实上，这个拖曳力包含一个作为张力分布曲线的下端边界的尾部张力，与缆索速度成线性关系

假设在速度为2.57 m/s时，TL=2 000 N，再者，假定角度的变化率为零，即

其中式（8）、式（9）中的L为缆索长度。根据式（8）和式（2）可以推断缆索在尾端的法向速度只是取决于横向海流。

结合上述条件，在模型的数值实现中，假设缆索横截面d是均匀的、各向同性的、弹性的且是不可伸长的，并忽略其剪切变形和动量项。

2正问题的数值解

应用有限差分法得到方程组（1）～（4）和（6）～（9）的数值解。特别地，首先，用时间上的有限差分将空间-时间问题被转化为一个空间上的两点边值问题，然后将得到的非线性微分方程用一阶泰勒级数展开来逼近，这样可以得到一个线性的两点边值问题。最后的代数方程组可以用牛顿法来解决［11］。Hughes［12］采用了一种基于广义梯形法的隐式格式。Gatti详细地论述了参数的选择对稳定性和精度的影响［13-14］。而Ablow使用的盒子方法（box method）是有条件稳定的［15］，Gobat和Grosenbaugh采取基于盒子方法的广义α算法，通过增强额外的时间均衡来校正不稳定性［16］。正问题的控制方程的矩阵形式及处理方法参见文献［17］。

在matlab对系统进行仿真，设定缆索的长度L=6 000 m，直径d=0.05 m。缆索被拖曳在船舶上，以恒速行驶。水的密度设定为1 025 kg/m3，切向和法向上的牵引系数假设为Ct=0.006，Cn=2。为了仿真海流，使用了三角功能的组合。在固定的直角坐标系中，海流的速度被缆索的长度和仿真器时间上的持续简单标准化如下

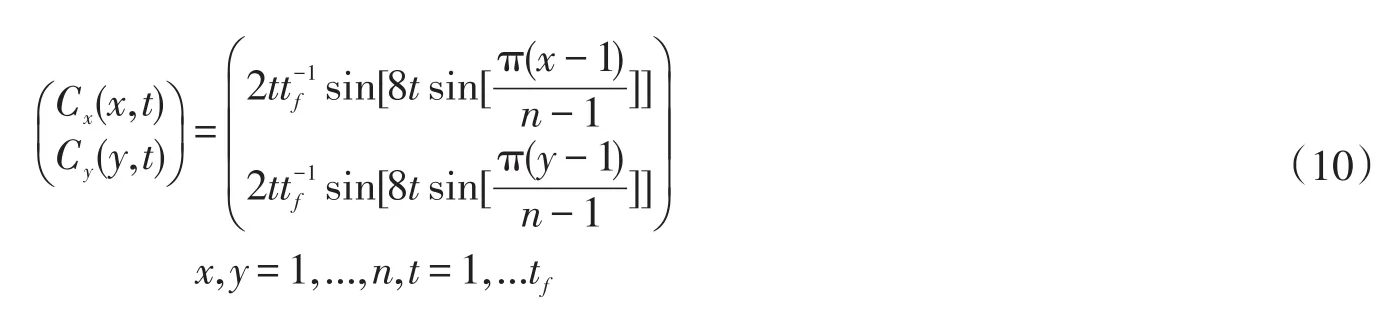
在本仿真方案的实施中，包含了一个由n=1 201个均匀分布成Δs=5 m缆元素的节点组成的网格。时间间隔设为Δt=10 s，仿真时间为0 s≤t≤3 000 s。仿真结果如图2所示，这些图形表示在连续流体动力激励下的张力和定位数据的连续空间变化。这个观察对于反向问题是很重要的，例如反向方法论的选择需要一个前置数据可辨性的预知。再者，因为根据预期，张力是一个严格递减函数，切向缆索速度保持平稳和负方向，这是切向坐标向量的默认方向也就是沿着缆索轴向的方向，而缆索的法向速度轮廓也是平稳的，虽然它似乎是一个更大变量。

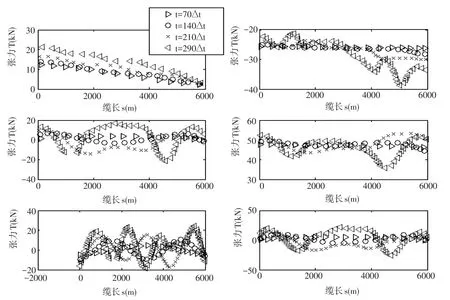
图2 在平滑变化的切向和法向水动力载荷下正问题的计算结果Fig.2 Calculation results of the forward problem under smooth change of tangential and normal hydrodynamic loads

3反问题简述

在前面的段落里，为了在拖曳数组观察系统中建立相对于海流速度的测量方法，通过方程式组（1）～（9），调查了正向的流体动力学模型。这样，前置模型认为缆索的形状和张力受流体动力干扰的影响。如果选择适当的边界条件，该系统的反应是唯一确定的（在无限空间里），也就是说，在一定边界条件下，在一个任意时间点，拖缆的空间形态与其所处的海流环境呈一一对应的映射关系。再换句话说，在一定条件下，可以根据这种一一对应的映射关系根据拖缆的空间形态及所受到的张力反推出其所处的海流环境。因此，可以根据这种特殊条件下的对应性和解决方法的唯一性对其进行离散。

可认为在任意一个时间点，认为有限空间的内射矩阵运算B，在一个由仪器和物理噪音总量设定的一个容忍值内映射海流的度量。这个总量用W=N（0，σ2）。

反问题的关键在于推断出一个纳入拖缆形态测量值的有限集去获得其对应的海流值，设这个集合为z=Z+W。式（11）中u和v的重建，主要依赖于前置运算的可逆性和篡改数据的噪音等级。模型方程式（1）和（2）的微分形式认为B是一个拟线性积分算子，它决定了一个由它的导数和一个边界条件给出的未知离散函数。实际上，B-1是一个线性微分算子，它可以映像一个函数给它的第一空间导数，这个本身是它固有缺乏的秩。这个表明在一个自由度是n的函数f中，它的导数f只能被自由度n-1唯一指定，尤其在这些样品n之间间隔的中点。结果，在由度量值n所给出的空间分辨率n度下的海流重建的反向问题是有秩亏的缺陷的，这对于这个方案的唯一性和稳定性有着直接的影响。对于这个工作的范围，它足够可以估算在n-1自由度下的海流流速分布，它可以构成一个所谓轻微的病态问题，因为虽然非唯一性是根除的，但是由于模型的微分形式之间的结合中的噪音数据的影响使得稳定性问题依然存在。噪音数据的求导是极不稳定的，在信号处理中，一直是被研究的对象。为了克服所提供的不稳定性正则化，建立了一个强大的B-1算子的近似值，要利用一个所要求的预知信息。

为了制定反向问题的正则化，需要引入2个动量方程（12）和（13），用在tilde里所引用的噪音数据来表示

对于测得的张力和曲率中的噪音内容，式（12）和（13）左边的导数达到标准，当Δs→0时，任意增长，这样的话，为了增强稳定性，用核心是Heavyside的阶跃函数的积分算子的逆分化改写方程式。

在一个有n个节点的有限网格上，算子以B∈Rn×n-1的矩阵形式导出动量方程式的积分公式

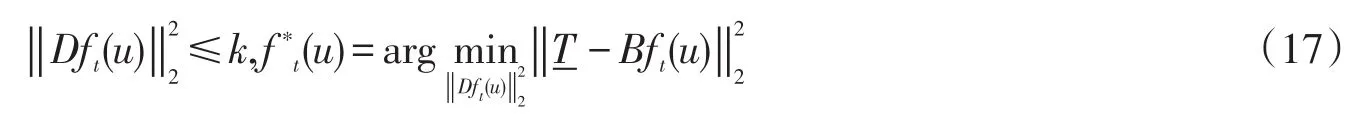
在上式中，D∈Rn-2×n-1是一个一阶差分算子的离散形式，附加上之后，所以对于一个非0的参数λ，吉洪诺夫公式承认了一个独特的解析值

根据切向流体拖曳力的定义，缆索上的内联流速分布可以计算为

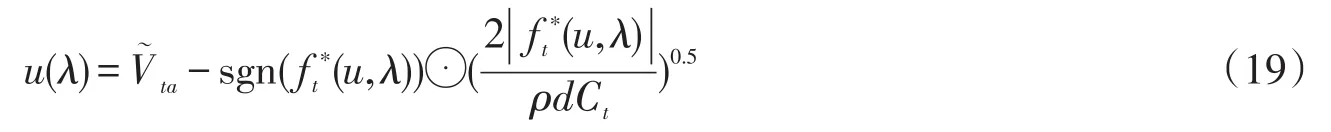
按照式（16）的类似程序，可以得到法向流体拖曳力的吉洪诺夫正则化的解决方案

在这里，⊙指的是元素级乘法，随后从以下方程序计算出十字流速

4奇异值和灵敏度分析

在反向问题的公式中，算子B和D，还有正则化因子λ，都扮演着重要的角色。在这个意义上，它们是密切相关的，差分算子将积分算子反转，正则化参数衡量它们在重建解决问题上的贡献。关于反向问题理论的详细分析出现在很多教科书中，这里不再赘述。对于这个工作的范围，它足够可以以他们的奇异值谱来证明两个算子的关系，这样可以帮助选择合适的λ。图3表示的是离散在一条6 000 m长的缆索上，有着601个等距节点的网格上的算子的奇异值。以指数方式衰减的奇异值B和以对数方式减少的奇异值D，它们之间的反向的相互作用确定为BDT=I∈Rn×n-2。

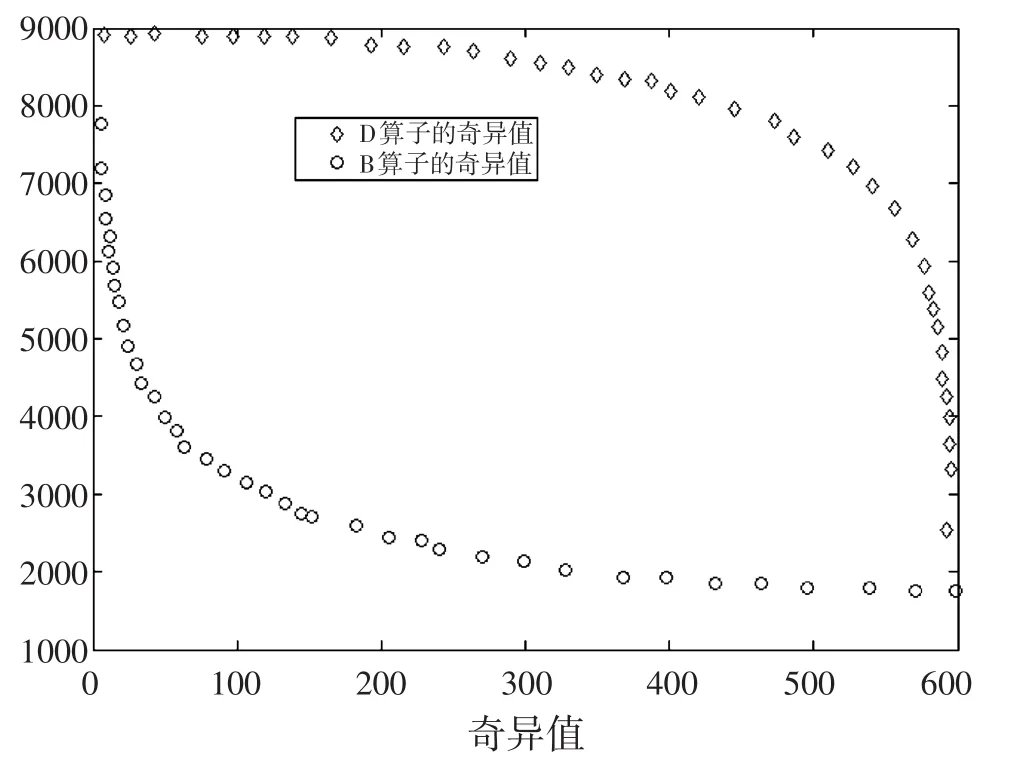
图3 B算子和D算子的奇异值Fig.3 The singular value of B operator and D operator

奇异值区间提供了一个对最优正则化参数的选择问题的深入了解。这个参数从基本上，利用式（17）中对于最小化目标的先前约束加权偏值，为之前和提取的测量信息之间，提供了必要的平衡。因此，这个选择必须和测量中的噪音水平、模型参数的不确定性和可用先前信息的可靠性保持一致。最优参数要满足在这里指的是奇异值，它利用L曲线法或者广义交互验证法来计算。

有些模型参数，比如缆索的长度和直径，可以精确的测量出来，但是有些很难准确的获得。例如在经过一系列的实验室控制实验后，拖曳系数Ct和Cn是分配值，虽然似乎有理由认为存在小小的不确定性，但还是应该更严谨的检查这种不确定性对反演方法性能的影响。从模型方程式中清楚的知道，Ct中的错误只对内联流速的计算值产生影响，Cn中的错误只对十字速度分量产生影响。

如果确切知道切向系数，那么，在认为无噪音存在的测量中，可以用一个给定的小值λ从式（19）中得到准确的内联流速u*。引入一个小的扰动值δ，所以Ct→Ct＋δ。

可以根据一个平方误差导出一个轮廓u

在这里，我们知道张力梯度总是负的。为了便于比较，对精确的法向拖曳系数用同样的摄动，比如Cn→Cn＋δ，计算出在十字线速度上的平方误差

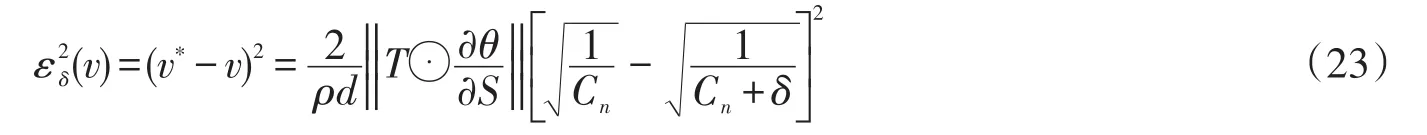
在这里，从式（21）中获得v*的精确值。当拖曳系数的标称值满足Ct≪Cn，很显然但是这不一定表明对于同样的δ来说，εδ(u)＞εδ(v)。事实上，公式中，张力对εδ(v)的影响是决定性的，虽然这关系到曲率的反比例，在和应用相关的角度范围中，因子T⊙∂θ/∂S可以任意大，尤其是朝着拖曳点。再者，Grosenbaugh中已经指出，在不稳定的拖曳运动中发生的流激振动，可能导致缆索的拖曳系数与它们的名义值有很大差异。特别是在切向上是多种多样的，法向系数改变是可能的，在运动中多达40％。在这种情况下，Cn上的大偏移可能对重建的十字电流产生误导的结果。为了避免发生这种情况，允许沿着缆索的拖曳系数的分布的不确定性在一定范围内，建议的反演方法需要在以稳健的参数估计下重新表示。

为了阐述在两个分量中的一个作为主导的重建速度剖面的过程中，反演方法的强大性和坚决性，进行了一些附加的模拟。在一个问题中，假设大的均匀速度CX（x，t）垂直于原先的垂直缆索配置，低幅度平滑变化的电流Cy（y，t）平行于初始柜道。假设在一个北上的直线轨道，以匀速2.57 m/s拖曳，设定CX（x，t）=10 m/s，Cy（y，t）=2 m/s（最大速度绝对值）。所得的法向拖曳力导致缆索逐渐偏离船舶轨迹，最终在一个大角度θ时，得到一个0度曲率配置。如图4的第一行所示，高法向速度的影响随着朝向末端的低张力，越来越大，调整它的形状可将法向流速的影响最小化。当θ增加时，图表显示缆索接近笔直，所以最终大部份投射在t轴上。在相反的情况下，流速主要平行于缆索时，张力增加，由于边界条件（8）使得张力梯度变化的绝对值增加，也使得曲率保持在一个低水平。图4最后一行所显示的结果已经用CX（x，t）=-10 m/s和Cy（y，t）=2 m/s（最大速度绝对值）计算出来，它们的拖曳速度和轨道是相同的。在这种情况下，决定形状和曲率的定位数据的精确性变得很重要，因为内联流速方法的灵敏度关系到在曲率变化中张力的产生，因此偏离直线轨道将意味着更高的法向流速。

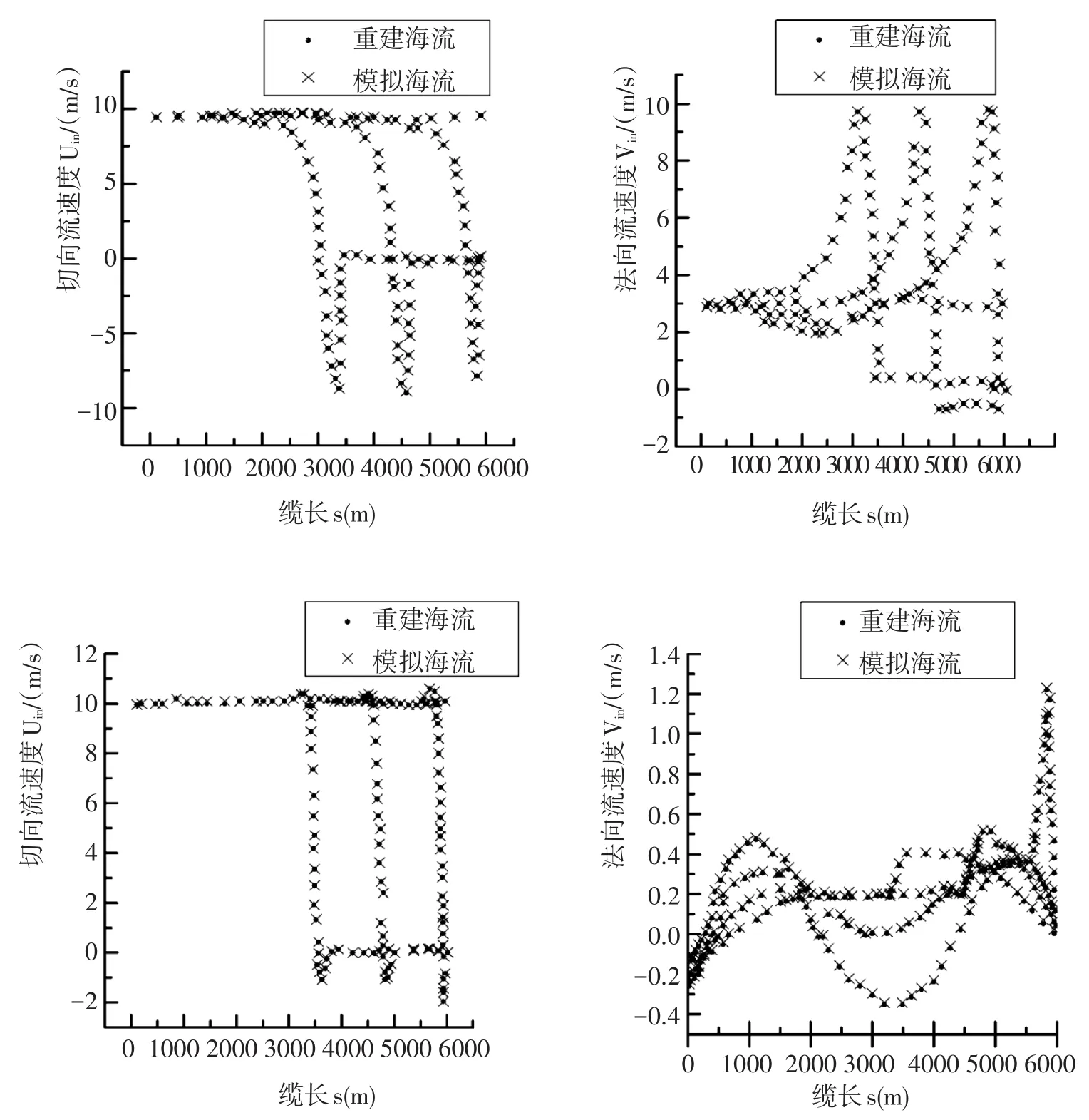
图4 在时间为60 s、80 s、100 s和120Δt时模拟和重现海流Fig.4 Simulation for reproducing of the current in time for 60 s，80 s，and 100 s and the 120Δt

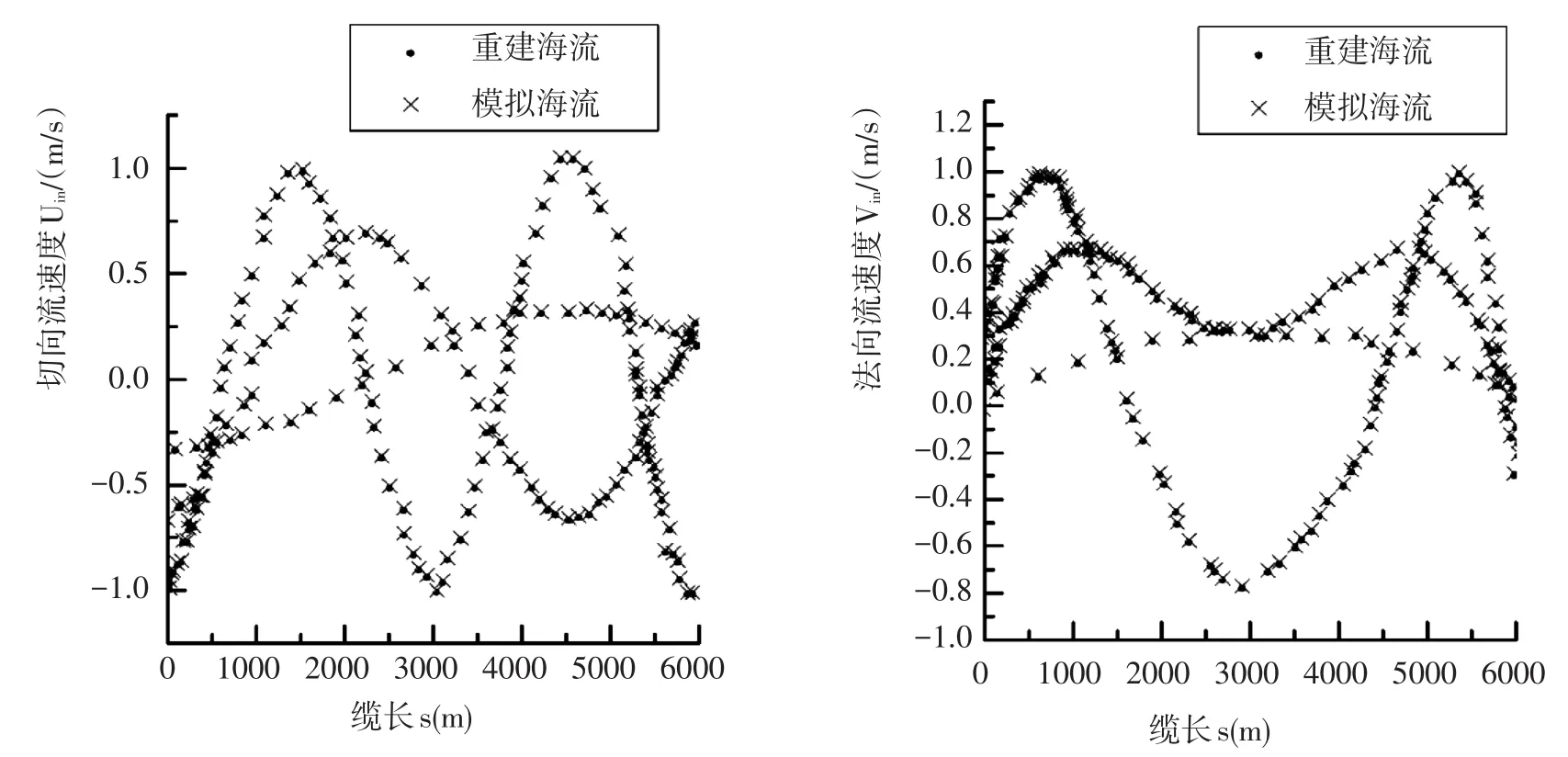
图5 无噪音时的计算结果Fig.5 Calculation results without noise

式（18）和（20）的重建公式清楚的表明了内联流速方法的敏感度完全依赖于沿着缆索的张力的梯度变化剖面的解决。从这个意义上，有着高杨氏模量的缆索在检测切向流速时将会提高灵敏度。换句话说，通过观察缆索的形状和关系到灵活度的曲率的改变，十字流速的检测是很明显的。所以，对于低刚度模量的缆索，预计在法向流速里有更高的灵敏度。

5结果和讨论

5.1无噪音数据的重建

在第一个例子中，我们认为理想的情况是，拥有无噪音的测量值，可以直接从模型方程式中恢复。无论是在（12）和（13）中使用FD计划来估算梯度变化，还是用零的正则化的积分方程式（18）和（20），都可以实现。选择后者，设定λ=0，得到了如图5所示的，在瞬时t=50.1 s和150Δt时的电流剖面。这些图表说明了在仿真和重建剖面之间有精确的匹配。这和关于第4部分中得到的积分算子的属性分析，是一致的。事实上，对于0正则化，采用Moore⁃Penrose pseudo⁃in⁃verse的形式，有n-1个非零的奇异值。这可与下一步要讨论的，在现实噪音水平下，反向方法的演绎作比较。

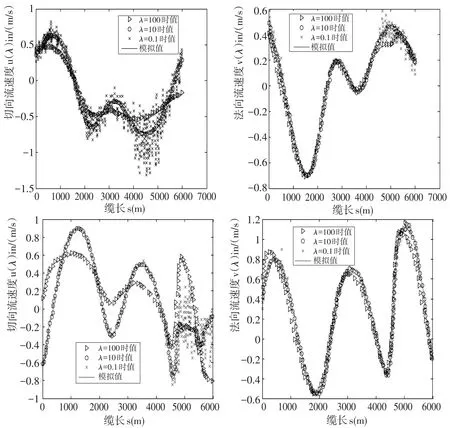
图6 有噪音σ1=0.01z时的计算结果Fig.6 Calculation results with noise for σ1=0.01z

图7 有噪音σ2=0.03z时的计算结果Fig.7 Calculation results with noise for σ1=0.03z

5.2重建噪音数据

当数据中注入添加的随机噪音时，正则化变得越发重要。在采集的真实观察数据中，这些数据因为仪器误差和物理噪音而被破坏，这种情况尤其会发生。为了模拟这些条件，在正向变量上引入一个伪随机白噪音信号W=N（0，σ12），在这里，σ1=0.01z，z指的是T，Vt，Vn和θ的平均值。当时间t=300 s和400 Δt时模拟的海流流速分布图如图6所示，还有正则化参数的不同值时的重建剖面。每一个图阐述了由吉洪诺夫方法获得的重建方案，为了阐述参数对于重建速度的空间分辨率的影响，它是利用（19）和（21），当λ=0.1，10和100时进行计算的。在所采用的广义吉洪诺夫方案中，根据D算子的选择所强加的之前光滑的假设，λ在反向问题中控制光滑度。

如果λ*是根据数据里的噪音内容的参数的最优值，图中所示的是利用一个λ（远远小于λ*）来规范内反向问题，这样噪音的影响更大。换句话说，如果选择λ（远远大于λ*）来规范外这个问题，可以有效的过滤解决方案中一些细节特征，因此可以让给空间分辨率。λ*=10的最优值是利用L曲线方法计算出来的。

观察图6中的这些图表可发现，对于所有的正则化参数值来说，法向分量v的重建，无论在定性还是定量上，都要比切向分量u的重建容易。事实上，这是合理的，因为尽管它们的公式相似，相比（18），反演公式（20）提供了一个更好更有意义的噪音鲁棒性。因为平均分布在向量中的张力，乘以原方程式中的正则逆曲率，会毁坏污染张力数据中的大部份噪音，而且因为默认（图2），对于（20）的噪音影响有限。

作为第二种情况，考虑到在更多的强噪音条件下的仿真数据，在运动开始以后，在时间t=500Δt和600Δt时被捕获。在模拟过程中，拖曳的船舶被设定为执行一个半径为3 000 m的圆形轨道，恒定速度为2.57 m/ s。注入测量值的噪音信号被设定为当σ2=0.03 z时，W=N（0，σ22）。正如之前，通过估算第一个最优正则化参数来计算沿着缆索的规则水动力载荷和速度。和预期的一样，随着数据中噪音水平的增加，需要通过增加光滑数量来稳定解决方案。L曲线法的实施产生了一个参数的最优值λ*=30。在时间t=500Δt和600Δt时的仿真速度和重建速度剖面如图7所示。和前一个情况的结果比较起来，最佳重建方案的空间分辨率u（λ*）和v（λ*）受到测量值中的噪声畸变的损害，而在切向分量的重建之前，影响是最大的。在同一个图中，也提供了一些用非最佳正则化所获得的反向解决方案，为了说明解决方案中参数的影响。特别是，对于λ＜1，施加在光谱B上的过滤总和不足以稳定解决方案，这个方法无法产生一个信息化解决方案。

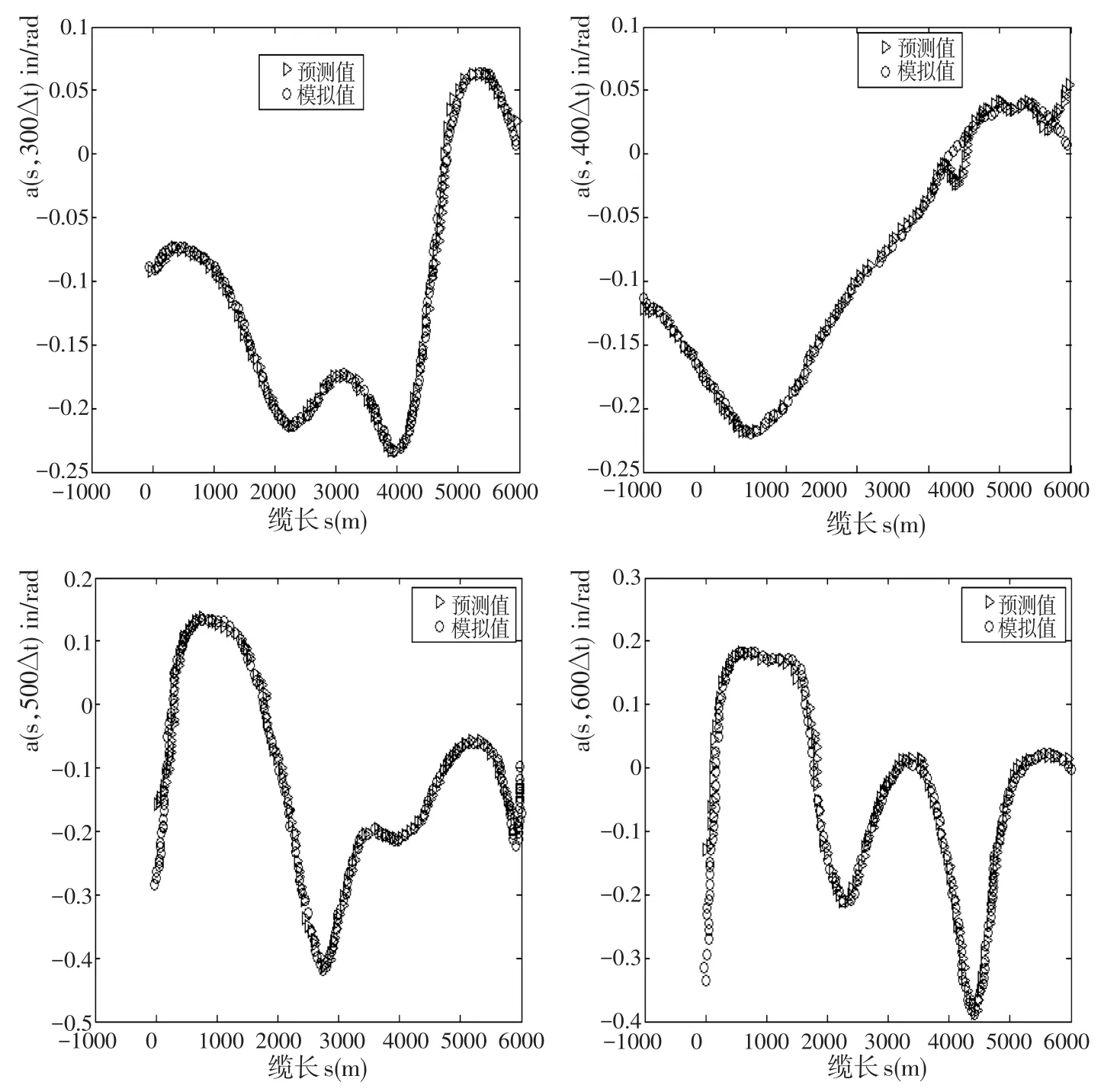
图8 重建海流攻角的预测结果Fig.8 The prediction results for the angle of attack at the reconstructed currents

5.3攻角或入射角预测

和缆索的最佳转向直接相关的拖曳数组是攻击角的估算和预测。正如在前一段中所描述的，海流流速分布图的重建为系统提供了一些重要的输入，可以控制缆索的转向，从这个意义上来说，攻角象征了这个信息。更精确的撞击飘带的海流速度信息可以产生一个攻角α的估计值

黑龙江省社科院孙文政研究员做了《海陵王瓜州失败始末及其原因》的报告。他认为，海陵王为了实现统一全国，做中国正统的皇帝，不顾金朝的实力，孤注一掷南伐灭宋，在瓜州惨遭失败。失败的原因是多方面的，既有主观原因，也有客观原因，既有历史的偶然性，也有历史的必然性。海陵王贸然发动统一全国的战争，不仅遭到宋朝军民的坚决抵抗，而且遭到金朝军民的强烈反对，以及宋、金双方战略战术上的差异，致使海陵王瓜州失败。

所以反馈控制角αc可以根据缆索转向预计的位置而调整，却不需考虑到海流。图8中，攻角α在时间t= 300 s、400 s、500 s和600Δt时，对于在最佳正则化下的第二个仿真数据，用仿真和预测的剖面制图。结果显示了在噪音条件下，模拟和预测剖面之间的良好协议，事实证明了反演方法在协助优化飘带转向中的效用。

6结论

（1）在正问题中，在缆索和拖船铰接的部位，拖船的速度就是缆索在此点的速度，而随着缆索离铰接点位置越来越远，且由于缆索本身为挠性结构，以上两种因素导致沿缆索长度方向某一位置的速度与拖船的速度相差越来越大。

（2）在一定条件下，当拖船航速不高（例如本文中的0.257 m/s），拖缆长度较长（例如本文中的6 000 m），在忽略弯曲刚度的前提下，当知道沿缆索长度方向的空间形态变化和张力变化时，可以解决海流流速剖面的反向问题。而如拖船拖速过高拖缆长度过短则由于不能充分得到足够的缆索空间形态的变化情况进而会造成不能充分将缆索的形状和样本值离散化，统计样本的不足使得此种方法不再适用。

参考文献：

［1］朱克强，李道根，李维扬.海洋缆体系统的统一凝集参数时域分析法［J］.海洋工程，2002，20（2）：100-105. ZHU K Q，LI D G，LI W Y.Lumped⁃parameter analysis method for time⁃domain of ocean cable⁃body systems［J］.The Ocean Engi⁃neering，2002，20（2）：100-105.

［2］朱艳杰，朱克强，杨冰卡，等.基于凝集质量法的海洋缆索动力学建模与仿真技术［J］.海洋工程，2014，32（1）：112-116. ZHU Y J，ZHU K Q，YANG B K，et al.Dynamics modeling and emulation technique of the marine cable considering tension and compression bending torsion deformation［J］.The Ocean Engineering，2014，32（1）：112-116.

［3］Choo Y，Casarella M J.Configuration of a towline attached to a vehicle moving in a circular path［J］.Journal of Hydronautics，1972（6）：51-57.

［4］Chapman D A.The towed cable behavior during ship turning maneuvers［J］.Ocean Engineering，1984（11）：327-361.

［5］Kishore S S，Ganapathy C.Analytical investigations on loop⁃maneuver of underwater towed cable⁃array system［J］.Applied Ocean Research，1996（18）：353-360.

［6］Mark A G.Transient behavior of towed cable systems during ship turning maneuvers［J］.Ocean Engineering，2007（34）：1 532-1 542.

［7］Gobat J I，Grosenbaugh M A.Application of the generalized a method to the time integration of the cable dynamics equations［J］. Computer Methods in Applied Mechanics and Engineering，2001，190：4 817-4 819.

［8］Hover F S，Grosenbaugh M A，Triantafyllou M S.Calculation of dynamic motions and tensions in towed underwater cables［J］.IEEE Journal of Oceanic Engineering，1994，19（3）：449-457.

［9］Milinazzo F，Wilkie M，Latchman S A.An efficient algorithm for simulating the dynamics of towed cable systems［J］.Ocean Engi⁃neering，1987，14（6）：513-526.

［10］Hui Z.Measuring ocean current from a towed seismic array at real time［D］.Manchester：UMIST，2005.

［11］Vogel C.Computational Methods for Inverse Problems［C］//SIAM.Frontiers in Applied Mathematics.Philadelphia：SIAM，2002.

［12］Hughes T J R.The Finite Element Method：Linear Static and Dynamic Finite Element Analysis［M］.New Jersey：Prentice⁃Hall，1987.

［13］Gatti C S C.Numerical simulations of large deformation cable dynamics［D］.Michgan：University of Michigan，2002.

［14］Gobat J I.The dynamics of geometrically compliant mooring systems［D］.Boston：MIT⁃WHOI，2000.

［15］Ablow C M，Schechter S.Numerical simulation of undersea cable dynamics［J］.Ocean Engineering，1983，10（6）：443-457.

［16］Gobat J I，Grosenbaugh M A.Application of the generalized a method to the time integration of the cable dynamics equations［J］. Computer Methods in Applied Mechanics and Engineering，2001，190：4 817-4 819.

［17］Milinazzo F，Wilkie M，Latchman S.An efficient algorithm for simulating the dynamics of towed cable systems［J］.Ocean Engi⁃neering，1987，14（6）：513-526.

Research of forward and inverse problems in towed cable hydrodynamics

ZHANG Da⁃peng1,ZHU Ke⁃qiang1,NIU Tian⁃xin1,WANG Zi⁃fa2
(1.Faculty of Maritime and Transportation,Ningbo University,Ningbo 315211,China;2.International Company, COOEC,Tianjin 300450,China)

Based on a two⁃dimensional model describing the motion of a flexible,inextensible cable in the pres⁃ence of hydrodynamic drag forces in an incompressible fluid,the problem of reconstructing the velocities of the ocean currents impinging on a towed streamer cable during an offshore seismic survey has been researched.Firstly, the forward model was introduced and then solved to get the cable′s velocity,curvature and tension in the knowl⁃edge of the towing vessel motion and the hydrodynamic loads applied.In sequence,the inverse problem of inferring the ocean current velocities from discrete samples of the cable′s shape and tension was formulated and the result shows that this is rank deficient and ill⁃posed.In approaching the inverse problem a numerically stable algorithm was adopted based on generalized Tikhonov regularization,in the context of robust differentiation of discrete noisy signals.In order to demonstrate the practical performance of the scheme,some examples of ocean current recon⁃structions obtained using simulated noisy data were presented.And it has certain guiding significance to the actual project practice.

towed cable hydrodynamics;ocean current velocity reconstruction;ill⁃posed inverse problem

TV 131.2

A

1005-8443（2016）04-0375-10

2015-12-15；

2016-03-24

国家自然科学基金资助项目（11272160）

张大朋（1987-），男，山东省聊城人，助理研究员，主要从事船舶与海洋结构物设计制造。

Biography：ZHANG Da⁃peng(1987-),male,assistant professor.