加强对比凸显本真<br/>——“扇形统计图”教学实录与思考

加强对比凸显本真
——“扇形统计图”教学实录与思考

2016-02-15金蕾红

教学月刊(小学版) 2016年14期

□金蕾红

加强对比凸显本真
——“扇形统计图”教学实录与思考

□金蕾红

扇形统计图是小学统计图教学的最后一部分知识。由于学生在日常生活中经常会见到扇形统计图，而且它表示各部分与整体的关系也比较直观，所以在教学中可以采取整体感知，实现简约的情境引入；一题多变，创设简约的练习资源；易错变式，提供简约的深度思考。自始至终采用对比的方法，引导学生认识扇形统计图的特点和作用，从而提高学生的数据分析的意识和能力。

扇形统计图简约练习资源

三年前，在市小学数学同课异构研讨活动中，笔者上了一节人教版课程实验教材六年级上册“扇形统计图”公开课。回想当时的磨课与上课的感触至今难忘，那时为了体现以生为本、以学定教的教学理念，努力追求简约高效的教学。最近笔者又一次教学此课，重新分析当时的教学，仍会感受到当时主要教学片段的设计非常精巧，但也发现有些素材的设计还比较零乱，尤其是课堂上的问题设计不够简洁。因此，笔者在原来设计的基础上作了进一步的改进，通过课堂实践收到很好的教学效果。现把这节课的教学实录和自己的思考作了整理，供大家教学时参考。

一、整体感知，实现简约的情境引入

【教学片段】

整体呈现条形统计图和扇形统计图（见下图），并引导学生自主解读。

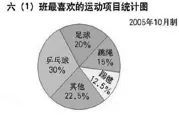
师:你能看懂这两张图吗？

生：从第一张图中我们可以直接看出六⑴班喜欢乒乓球的人数最多有12人，喜欢踢毽的人数最少只有5人。

师：第一张图我们说它是什么统计图？

生：条形统计图。

生：从第二张图中也可以看出喜欢乒乓球的人数最多，喜欢踢毽的人数最少。

师：为什么？

生：从第二张图可以看出喜欢乒乓球的人数占全班总人数的30%，占的百分数是最大的；而喜欢踢毽的人数只占全班总人数的12.5%。

师：第二张图中表示全班总人数的是哪部分？

生：这整个圆表示全班人数。

师：整个圆表示全班总人数，根据各种运动所占的百分数画出大小不同的扇形，这样的统计图叫作扇形统计图。那第二张图中的百分比是怎样算出来的？

生：是根据各项的人数除以全班总人数算出来的。

师：好的，那我们根据第一张图中的数据，计算喜欢乒乓球的人数是否占全班总人数的30%？喜欢踢毽的人数是否占全班总人数的12.5%？（学生计算后作了反馈交流）

师：条形统计图是我们过去学过的，它与今天学的扇形统计图各有什么优点呢？

学生分小组讨论教师提出的问题后，再组织集体交流，使学生明白：第一张条形统计图能直接看出各种运动项目人数的多少，但不能看出部分占总数的百分比。第二张扇形统计图能看出各种运动项目占全班总人数的百分比，它不仅能较快地看出部分与总数的关系，还能比较出各部分所占百分比的多少，但它不能看出具体的人数。

接着教师又提出：你知道这个扇形统计图是怎样画出来的吗？

生：先画一个圆表示全班人数，然后再根据各种运动项目的百分比来画扇形。

师：哪各部分的扇形又是怎么画呢？

学生进一步观察思考着，慢慢地提出：要把各部分扇形的圆心角定下来就可以了。

接着教师借助于投影，让学生观察各种运动项目扇形的圆心角的计算过程（即圆周角360°乘相应的百分比）；同时逐步演示各种项目扇形的画法过程。

【思考】原人教版实验教材先呈现的是条形统计图，再呈现例题的扇形统计图；而新人教版义务教育教材先呈现的是统计表，根据各种运动项目的人数与全班人数，让学生算出各种项目所占的百分比，再去填写扇形统计图中部分所占的百分比。教材编写各有优点，修改后的教材关注的是通过计算各种运动项目所占的百分比，强化了部分与整体的关系。修改前的教材关注的是把已学过的条形统计图与扇形统计图进行及时的联系与区别。笔者觉得扇形统计图是学生在小学阶段认识的最后一种统计图，它与条形统计图的比较很有必要。所以在以上的教学中还是采用了原实验教材的素材，但在教学上没有采用原教材分前后的方式来呈现，而是将条形统计图与扇形统计图同时展示给学生。让学生自己去观察、比较、质疑、交流，学生在自主解读它们的联系以及区分它们功能的过程中，自然生成对扇形统计图的认识，从而达到知识的整体建构。

二、一题多变，创设简约的练习资源

（一）利用例题资源，引申计算

接着屏幕上隐去条形统计图，只剩下例题（扇形统计图），教师向学生提出：在这张统计图上我们知道喜欢乒乓球的人数占30%，不能看出喜欢乒乓球运动的人数，那告诉你什么信息，你就能知道喜欢乒乓球运动的人数？

生：总人数。

师：现在老师告诉你喜欢足球的人数是8人，你能求出喜欢乒乓球的人数吗？（学生独立计算后，组织交流评讲）

生：8÷20%×30%=12人。

师：你是先算什么？为什么要这样计算？

生：第一步计算的是全班人数，因为喜欢足球的人数是8人，占全班的20%，所以“足球人数÷20%＝全班人数（40人）”。（师随机板书这个关系式）

师：第二步就是求出了“全班人数×30%＝乒乓球人数（12人）”。

师：如果已经知道了全班人数是40人，你们能以最快的速度计算出其他三个项目的人数吗？

学生计算后，互相检查结果。接着教师小结：同学们，扇形统计图虽然各部分数量看不出来，但它可以很直观地看出各部分数量与总数的关系。所以只要告诉我们其中一个数量，我们就可以利用关系把各部分的数量算出来。

【思考】本环节是对例题的进一步开发利用，针对刚认识的统计图提出了相关的计算，有利于学生对扇形统计图加深认识。

（二）创设比较资源，辨析特点

投影呈现以下三张表格，并向学生提出：以下三张表格都讲的是光明小学的植树问题，想一想，你觉得哪张表格的数据可以选用画扇形统计图的方式来呈现？

学生经过观察、互相交流后，说出根据第三张表格中的信息，可以把它画成扇形统计图。

光明小学2015年各种树木数量统计表

光明小学2011～2015年树木总量变化情况统计表

光明小学2015年各种树木数量所占百分比情况统计表

师：为什么第三张表格中的信息可以画成扇形统计图呢？

生：因为在第三张表格中告诉我们的是各种树占总棵数的百分比。

师：是的，第三张表格中的信息是各部分与总数的关系，所以要选择扇形统计图。根据第三张表格中的信息画扇形统计图，你觉得应该把表格中的信息填入下面哪个图？

学生根据第三张表格中的信息，选择了第⑶个图。

师：为什么要选择第⑶个图呢？

生：因为柳树和其他树各占了总数的25%，这两项合起来刚好是50%，所以先选择圆的一半。接着再观察杨树占30%，比25%要大一些。第⑶个图刚好符合以上条件。

师：好的，真不错，你们能根据第三张表格中百分比的大小来分析图中各部分扇形的大小。那根据第一张和第二张表格中的信息，又应该去画什么统计图？

学生回答出第一张适合画条形统计图，第二张适合画折线统计图后，教师要求学生阐述选择不同统计图的理由。接着在投影上呈现相应的条形统计图和折线统计图。

【思考】在这一环节，笔者给学生提供了同一植树问题为背景的三张表格数据信息，先让学生选择哪张表格的信息适合画扇形统计图。当学生选择出第三张表格适合画扇形统计图后，紧接着笔者马上让学生针对第三张表格信息选择应该画成怎样的扇形统计图，这样使学生在比较中再次认识扇形统计图的特点，进一步辨认各部分与总数的关系。与此同时，在以上的教学中，笔者还要求学生针对第一张和第二张表格中的信息选择什么统计图，这也是把小学所学的三种统计图作了整体辨析，提高了学生针对具体问题具体分析的能力，促使学生自主构建完整的知识体系。

三、易错变式，提供简约的深度思考

师：刚才大家根据表格的信息数据，辨析了三种统计图的应用特点，下面你还能根据以下两张表格中的数据，分别确定用什么样的统计图吗？

阳光小学六年级每班抽测20人中的体育达标情况统计表

阳光小学六年级各班人数情况统计表

大部分学生都认为第一张表适合扇形统计图，第二张表适合条形统计图，少数学生提出质疑。

生：不对，第一张表格虽然是用百分数表示，但是每一部分都是独立的，不是各部分同总数之间的关系，同时各部分百分数相加的和也不是100%。

生：第二张表格表示各班人数的多少，只能适合用条形统计图来表示。

生：第二张还可以用折线统计图来表示。

生：不能用折线统计图，因为各班人数是没有关系的，所以不能用折线统计图。

师：是的，各班人数是互相独立的。只能用条形统计图。那根据第一张表格的信息，要画统计图，应该画什么统计图？

生：只能画条形统计图。

师：把这两张统计表的数据信息合起来考虑，你们觉得每班都抽出20人来检测达标率合理吗？为什么？

学生进行分组讨论后，提出两种意见：有一部分学生认为是合理，而另一部分学生认为不合理。

认为合理的同学认为都是抽出了20人，每班抽测的人数相等。

认为不合理的同学认为各班的人数不一样，抽测的人数也应该不一样。

师：这四个班的总人数是200人，每班抽了20人，共抽了80人，相当于抽出的人数是六年级总人数的40%。现在你们再想想，每班都抽20人合理吗？

生：各班都应该抽出自己班级人数的40%。

这时教师在投影上呈现出一张如下表的表格，让学生根据班级人数填出抽测人数，并提出按这样的人数去检测相对精确一些。（达标需要检测后再填写）

阳光小学六年级按各班人数的40%抽检体育达标率统计表

师：如果要求大家根据以上表格的数据信息画扇形统计图可以吗？

学生经过小组讨论后得出：要画扇形统计图，先要计算出各班人数占全年级的百分比。

师：好的，请大家计算填好下面的表格，再画出扇形统计图。

学生分别计算出各班人数占全年级的30%，25%，25%，20%，然后在右边圆中画出各班所占的扇形（圆周已等分成10份，便于学生画出各部分的扇形）。

【思考】学生学习扇形统计图，最容易看到了百分比就误认为可以画扇形统计图。因此，笔者特意在本环节给出的第一张表是各班达标率的统计表。果然一部分学生就出现了错误，但我们让学生在纠错的过程中达到了对扇形统计图加深认识的目的，使学生在头脑中牢固建立扇形统计图一定是反映各部分占总数的百分比关系。在接着的教学中，笔者还特意向学生提出按每班抽取20人来检测合理吗？引发学生在质疑中深入思考，逐步明确了抽取的样本的百分比要相同，要根据各班人数的多少来抽取检测人数。这一环节的教学处理也使学生初步领悟到统计与概率的联系。最后笔者还要求学生根据第二张表格各班的人数，计算出各占全年级人数的百分比，再根据百分比画出扇形统计图。通过学生的独立填算和画图，进一步加深理解扇形统计图的特点和作用。