从“正常水平的发挥”到“平均数”的理解*——“平均数”的前概念研究

□俞正强

从“正常水平的发挥”到“平均数”的理解*
——“平均数”的前概念研究

□俞正强

编者按

前概念研究

本刊在2016年1～2期对吴卫东教授及其团队关于小学生数学学习前概念研究的部分成果进行了展示，为教师提供了较好的教学参考，本期继续刊登其教学实践成果，欢迎教师加以关注。

平均数是一个学生易学会用，却难以理解的数学概念。但在学生的经验中其实有这样一个概念，这个概念就是“正常水平或正常发挥”，与超常和失常相连。教学的任务便是发现并建立两者之间的联系，理解便自然而然了。

平均数 正常水平 超常（失常）水平

平均数，从学生数感的发展而言，是对虚拟数的第一次理解。因此，如何让小学生理解“平均数”这一概念是十分值得研究的。

一、我们现在这样教

通常我们在课堂教学中，学习平均数会从一个事例开始，如下面所设事例。

材料：

男生组投篮统计

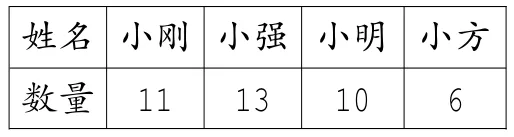
姓名小刚小强 小明 小方数量 11 13 10 6

女生组投篮统计

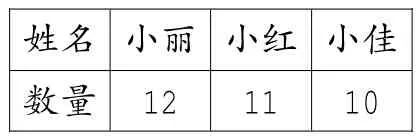
姓名 小丽 小红 小佳数量 12 11 10

问题：哪一组的水平高？

设计这份材料与问题的意图是基于对平均数的一种认识。

学生进行大小比较或水平比较的发展流程是这样的：

发展水平一：“单个间”的水平比较，比单个的多少。比如甲投中7个，乙投中6个，甲的水平高。

发展水平二：相同个数“组”的水平比较，比相同成员间的总数。比如甲组7个和9个，相同个数的乙组8个和10个。7+9与8+10比较，和大者水平高。

发展水平三：不同个数“组”的水平比较，此时如果比成员间的总数不公平，这就需要比平均数。

这个认识的结果是学生在学习平均数时，他们的认识主要有以下两部分内容：（1）平均数的用途是公平地比较两组成员之间的水平高低。（2）平均数可以通过总数除以份数来求得。

二、“平均数”的概念在哪里

知道平均数的用途，是平均数的概念吗？

知道求平均数的方法，是平均数的概念吗？

平均数的概念有两个要点：（1）它是代表一组数的整体水平。（2）它具有虚拟的特征。

就知识的完整性而言，它应该包含以下内容：概念蕴含着方法与应用；因为具有虚拟性，所以平均数的得到需要总数除以总份数或者移多补少；因为平均数代表整体水平，所以平均数可以用来比较两组数的水平，具有统计价值。

正确的学习方式应该是这样的：从学生的生活中去寻找关于平均数的前概念；从前概念中生长出平均数的概念；从平均数的概念中生长出平均数的求得方法；从平均数的概念中生长出问题解决的应用。

而我们目前的教材中则省去了概念的学习。直接在应用与计算中学习概念，而这样的概念学习事实上是淹没于计算与应用中了。

所以，这样的学习，往往是知其然而不知其所以然。

三、“平均数”的前概念是什么

学生的生活中有平均数吗？特别是十岁前的儿童生活中有平均数的前概念吗？

这个问题困惑笔者许久，后来发现学生经常讲以下三个词：超常发挥、正常发挥、失常发挥。

这三个词，学生更多地用在吃、跑和考试中。

笔者发现，这三个词可以分别对应我们在数学中将要学习的统计概念。于是，笔者选择了学生关于跑步的经历来帮助学生建立“平均数”的概念。

四、从“正常发挥”到“平均数”

材料：二年级小朋友60米跑了五次，时间分别如下（单位：秒）：15，14，12，10，14。

他填以下这张表：

60米，我大约要跑____秒。

问题一：

这位小朋友填了15，却又把15画去了，同学们知道为什么吗？

60米，我大约要跑15秒。

学生回答：太慢了，不好意思。

问题二：

后来，这位小朋友填了10，一会儿又把10也画去了，同学们知道为什么吗？

60米，我大约要跑10秒。

学生回答：10秒是最快的，是超常发挥的，他生怕自己以后跑不起。

问题三：同学们，那大家认为，这位小朋友最好应填几？

学生回答为以下三种：

1.14，因为跑的次数最多。

2.12，虽然14跑的次数最多，但偏慢了，偏慢不如偏快。

3.13，不快不慢，刚刚好。

说明：平均数的第一个内涵出来了：13代表这组数的水平刚刚好，不快不慢。

问题四：13秒。这位小朋友根本没有跑出来过，填上去是不是不诚实啊？能填吗？

学生们的争议将本节课推向高潮。

观点一：不能填，因为没有跑出来过。

观点二：可以填，现在没有跑出来，不等于第七次不会跑出来。

说明：虚拟的特征已经成为学生们理解的对象。

问题五：13没有跑出来过，13跟这些跑出来的数之间存在怎样的关系呢？

关系一：（15+14+12+10+14）÷5=13

关系二：

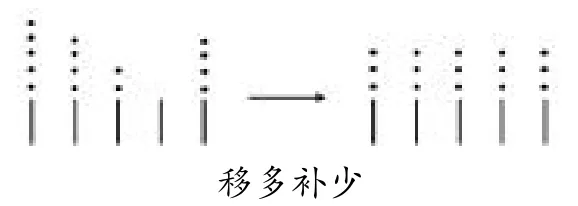
结论：原来13藏在这些数中间。

说明：平均数的计算方法便自然出来了。

五、“平均数”的概念习得

将上述讨论整理成以下材料：

60米我大约要跑15秒最慢

10秒最快

14秒次数最多但偏慢

12秒偏快

13秒刚刚好，但没跑出来过

问题：同学们，这几个数的特点，你认为哪个数最有意思？

学生回答：13最有意思，它有两个特点：刚刚好表示水平；没有跑出来过但蕴含在其中。

结论：这种数我们称它为“平均数”。

从上课的过程来看，学生对平均数的理解是跌宕起伏的。没有跑出来过，却正好表示水平，成了学生最大的纠结。而这种纠结正是不愤不悱的真实状态：所有这些，均来自生活中的关于正常、失常、超常的理解。

因此，将正常水平作为平均数的前概念是有实践意义的。

（浙江省金华市金师附小 321000）

浙江省哲学社会科学重点课题：小学生数学学习前概念诊断与教学干预研究（13NDJC007Z）