VaR和ES的贝叶斯经验似然估计

张军舰，赖廷煜，杨晓伟

(广西师范大学数学与统计学院，广西桂林541004)

VaR和ES的贝叶斯经验似然估计

张军舰，赖廷煜，杨晓伟

(广西师范大学数学与统计学院，广西桂林541004)

风险价值(VaR)和预期亏损(ES)能较好地度量金融投资组合的最大损失，研究其估计具有重大意义。本文利用贝叶斯经验似然方法对VaR和ES进行估计，理论上讨论了该估计的相合性和渐近正态性。模拟结果显示，在合适的先验信息下，本文所提出的估计具有一定的优势，有较好的应用前景。

风险价值；预期亏损；贝叶斯经验似然

0 引言

风险度量在金融市场中具有非常重要的作用，对其进行科学度量是一项非常重要的工作。目前比较流行的风险价值(VaR)和预期亏损(ES)就是其中的2种度量，它们能较好地度量金融投资组合的最大损失，因此对其进行精确估计对投资管理有重大意义。为克服传统风险度量的缺陷，1993年西方G30集团提出用VaR来度量市场风险，随后文献[1]给出了较权威的定义：在正常的市场条件和一定的置信水平1-p下，VaR表示在未来一定持有期内某投资组合或金融资产的最大损失量。从统计学的角度看，可以认为VaR相当于损失分布的上p分位数，数学表示为：

P(Y>VaRp)=p，

其中Y表示投资组合或金融资产的损失量。置信水平1-p反映了投资者对风险的喜好程度。

VaR定义简单，但在现实应用中却存在一些不足。首先，VaR不是凸性风险计量，不满足次可加性， 因而最小风险的投资组合不能通过优化方法来求；其次，VaR对尾部损失估计不充分，特别是厚尾分布的情况，致使投资者由于忽略微小概率事件发生而导致巨大损失。为了充分估量尾部损失， 文献[2-3]提出了条件VaR(CVaR)，其定义为：

CVaR=E(-X| -X>VaR)=-E(X|X<-VaR)，

其中X表示某投资组合或金融资产在特定的持有期内的收益率。文献[4]定义了损失函数为一般分布情况的CVaR。从上述定义看，CVaR实际上是一个条件期望，它是局部损失的平均值，CVaR克服了VaR的上述不足，它是凸性的风险统计量，而且文献[5]证明了CVaR是一个一致性风险度量，即满足单调性、正齐次性、平移不变性、次可加性，可以作为优化投资组合的工具。文献[6-7]提出要以CVaR代替VaR作为金融机构的风险管理工具，并对VaR进行改进，提出较为广泛的预期亏损(ES)指标来度量风险，同时证明ES也是一致性风险度量。ES定义如下：

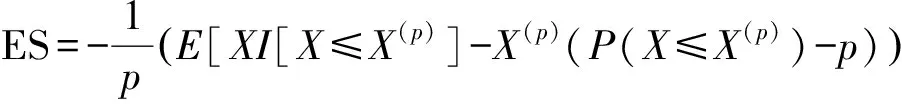
其中：X表示某投资组合或金融资产在某一特定持有期内的收益率；X(p)表示X的p分位数；I[·]表示示性函数。虽然ES的定义看上去较为复杂， 但其考虑更为全面。当事件概率P(X≤X(p))>p时，ES对估计不足的那一部分损失也进行了计算；而当收益分布是连续分布时，CVaR与ES是一致的。

近几年，对VaR和ES的估计是统计学家和金融专家非常关心的一个问题，讨论的文献也比较多，此处不再一一细说，具体可参见文献[8]及其参考文献。本文计划采用贝叶斯经验似然这种非参数方法对这2个指标进行估计。事实上，经验似然是由文献[9]提出，它具有参数似然方法的优良性，并且用经验似然构造的置信区间有域保持性、变换不变性、区间置信域形状由数据自行决定、Bartlett纠偏性以及无需构造枢轴量等优点。其后讨论的学者较多，详见文献[10-13]。另一方面，贝叶斯估计把先验信息跟样本信息结合起来，充分利用已有的信息去推断结果。如果处理先验信息的方法得当，那么就有可能提高估计的精确度。把贝叶斯和经验似然结合起来使用，直觉上它能保留之前的一些优良的性质，又能提高估计的精度。这种思想已被部分学者注意到，例如文献[14]提出贝叶斯经验似然方法， 并把它用于期望的推断；文献[15]把贝叶斯经验似然用于分位数回归估计；文献[16]把贝叶斯经验似然用于复杂抽样等等。尽管讨论文献较多，但用此思想对风险度量进行研究的几乎没有。本文拟在前人的基础上，用贝叶斯经验似然对VaR和ES进行估计，然后探讨其相应的性质，并做一些模拟比较。

1 VaR和ES的贝叶斯经验似然估计

假设X1，X2，…，Xn是从真实分布为X～F中抽出的独立收益率样本，置信水平为1-p的VaR值记为q，ES值记为μ。为行文紧凑，我们把VaR和ES合在一起考虑，主要讨论收益率是连续分布的情况，这时ES=CVaR。令Q表示X的p分位数，

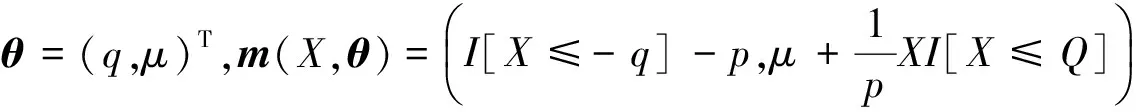
θ就是我们将要估计的参数，m(X，θ)即为文献[11]中所给出的无偏估计方程。类似于文献[15]的思想，可以构造θ的经验似然比函数为：

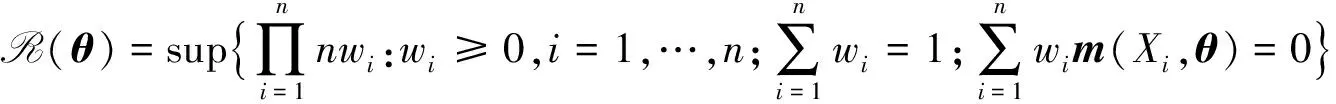
利用拉格朗日乘数法求得：

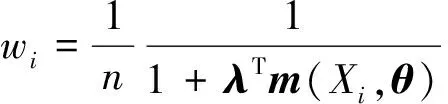
其中λ满足：

(1)

此时，

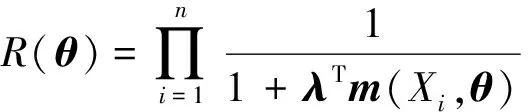
(2)

其中λ=λn(θ)满足式(1)。θ的点估计可以用

(3)

获得，它是获得θ的后验密度函数的先决条件。

假设θ的先验分布为p0(θ)，把先验分布跟经验似然函数结合起来得到θ的后验密度函数为：

p(θ|Xi，…，Xn)∝p0(θ)×R(θ)。

(4)

R(θ)见式(2)。θ的点估计可以考虑用θ的后验期望E(θ|Xi，…，Xn))去估计。由p(θ|Xi，…，Xn)也可以求出θ的置信水平为1-α的置信区域。如果其后验密度的精确分布不易求得，可以找其极限分布，进而利用其极限分布求得相应的置信区域。

条件1：存在包含参数真值θ0的邻域I，使得对任意的θ∈I，有p(R(θ)>0)→1。

条件2：分布函数F(x)关于x二阶连续可导。

条件3：在真值θ0=(q0，μ0)T某个邻域内， 密度函数F′(t)=f(t)>0。

条件4：E{m(X，θ)mT(X，θ)}正定。

条件5：log{p0(θ)}的一阶导数在θ0的某个邻域有界。

这些条件是保证似然函数的光滑性， 使得后验分布函数可以展开。条件1保证凸包有解；条件2是保证解唯一；条件4是保证先验分布部分可以泰勒展开。

定理2 在条件1～5下，后验分布密度函数p(θ|xi，…，xn)在{θ：θ-θ0=O(n-1/2)} 上可以展开如下：

(5)

2 模拟分析

本节我们取常见的正态分布对VaR和ES进行模拟计算。先固定样本容量n， 探究不同的先验分布对结果的影响，然后对不同的样本容量n， 比较贝叶斯经验似然和经验似然方法的覆盖率和置信区间平均长度。为书写方便，贝叶斯经验似然方法用BEL表示，经验似然方法用EL表示。

首先考虑VaR置信区间和覆盖率的模拟。我们给出的模型和条件如下：取收益率分布为正态分布， 样本由正态分布N(1，1)产生， 此时置信水平为1-p=0.95的VaR=0.644 8。为了考察不同的先验分布对结果的影响， 我们取VaR的先验分布分别为正态分布N(0.644 8+a，b)，其中a=0，1/n， 1/n1/2，3/n1/2，2；b=1/n，1/n1/2，1，n。重复模拟次数N=10 000，VaR置信区间的置信水平取为1-α=0.95。

固定样本容量为n=200，用上述的先验分布模拟计算VaR的覆盖率和置信区间平均长度。为了便于比较，我们也计算了在相同样本容量下经验似然方法的覆盖率和置信区间平均长度，分别为94.14%和0.615。具体模拟结果见表1～3。

表1和表2分别对应于不同的先验分布下所得到的置信水平为1-α=0.95下VaR的置信区间的平均长度和覆盖概率。由表1和表2可以看出，整体上贝叶斯经验似然方法的置信区间平均长度比经验似然方法的置信区间平均长度要短，覆盖概率要略低于经验似然的覆盖概率，但相差不是太大。另外，当先验分布的方差为1/n时，置信区间平均长度要比其他的短。当先验分布的参数的取值接近于真实情况时，有较高的覆盖率和较短的区间长度，而且方差越小，覆盖率越高，置信区间平均长度越短。当均值偏离真值时，覆盖率下降，特别当均值偏离较远方差较小时，覆盖率非常差。这种情况跟现实情况对应，我们集中取了一个错误的先验信息去推断结果，结果当然是非常糟糕的。

表3对不同的样本容量n， 比较VaR的置信水平为95%的置信区间的BEL和EL方法的覆盖率和置信区间平均长度。先验分布取接近真实参数，为N(0.644 8，1)。由表3可以看出，当先验分布的参数接近真值时，BEL方法的覆盖率与EL接近，但区间平均长度小于EL。样本容量n较小时，比如n=100，BEL方法的覆盖率比EL高，置信区间平均长度也比EL短。随着样本增加，二者越来越接近。这跟直观上相符合，当样本容量变大时，样本信息的作用增加，而先验信息的作用减弱，这样贝叶斯经验似然方法逐渐靠近经验似然方法。

表1 VaR的置信区间平均长度(样本容量n=200)

表2 VaR的置信区间覆盖率(样本容量n=200)

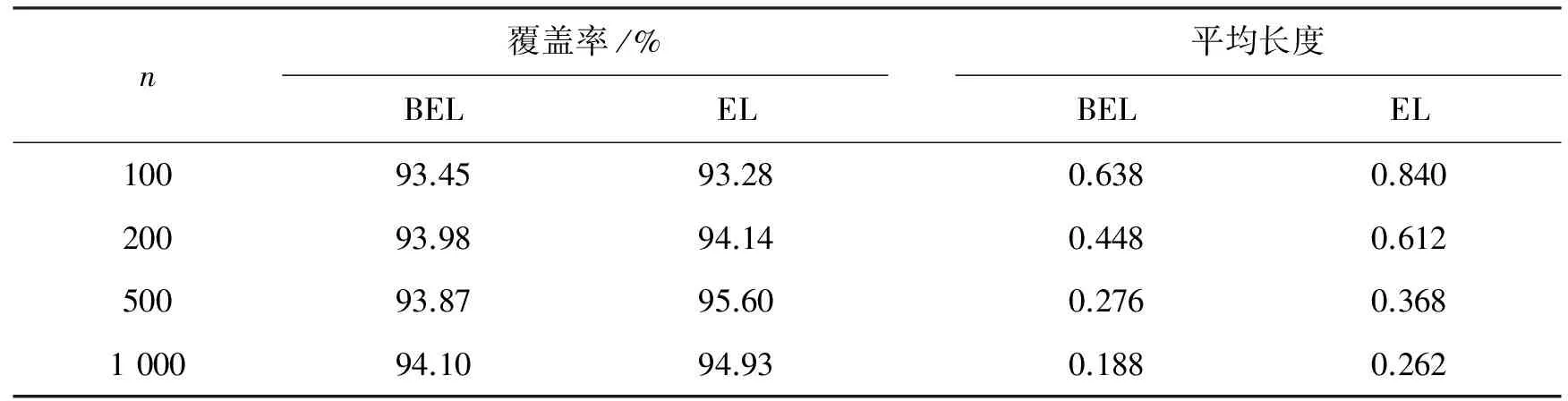
表3 VaR置信区间的覆盖率和平均长度比较

下面考虑ES的置信区间模拟。对于ES也有上述关于VaR的类似模拟结果，这里主要模拟在较小样本，先验信息较准确情况下，比较BEL和EL方法的优劣。

模拟的模型和条件如下：

①模型：假设投资组合或金融资产收益满足正态分布，样本由正态分布N(1，1)产生， 此时， 置信水平为1-p=0.95的ES=1.062 7，ES的先验分布取正态分布N(1.06，1)。

②条件：样本容量n分别为10、20、50、100；模拟重复次数N=10 000；置信水平为1-α=0.95。

所得到的模拟结果如表4所示。从表4可以看出，贝叶斯经验似然方法的置信区间的平均长度总是小于经验似然方法，而覆盖率大部分情况高于经验似然，或者非常接近。

表4 ES置信区间的覆盖率和平均长度比较

3 主要结论的证明

本节给出第1节中2个定理的证明。我们的证明过程与文献[14]方法相似。为使证明易于阐述，我们先证明以下引理。

引理1 在条件2下，我们有下面结论：

①E{m(X，θ)}和E{m(X，θ)mT(X，θ)}关于θ是二阶连续可导的。

②存在θ0和λ=0的紧邻域Dθ、Dλ，在此邻域内E[m(X，θ)/{1+λTm(X，θ)}]关于θ和λ是二阶连续可导的，E{m(X，θ)mT(X，θ)/[1+λTm(X，θ)]}关于θ和λ是一致连续的。

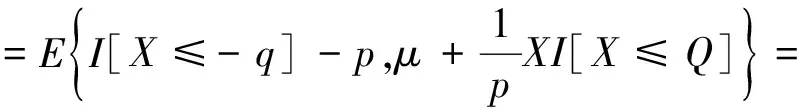
由于M=m(X，θ)mT(X，θ)是一个2×2的矩阵，

EI2[X≤-q]-2pEI[X≤-q]+p2=

F(-q)-2pF(-q)+p2，

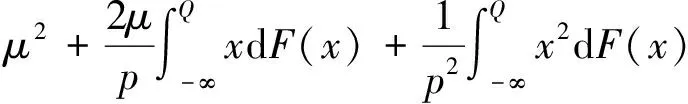
由条件2，F(x)是关于x的二阶连续可导函数， 结合上面式子，E{m(X，θ)}和E{m(X，θ)mT(X，θ)}关于θ是二阶连续可导的。

引理2 (ⅰ)常数函数类：C0={λ|λ∈D}为P-Glivenko-Cantelli(P-G-C)类，其中D为R上的某个紧集。

引理2由文献[14]中引理3修改而得，证明详见文献[14]。

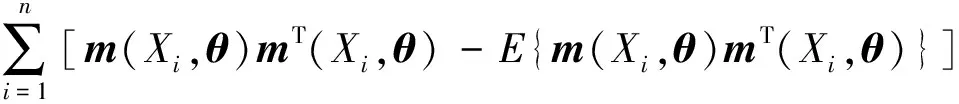
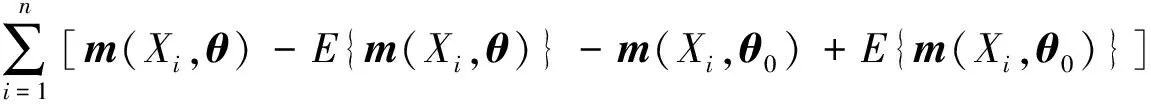
证明 因为估计函数m(X，θ)是P-Donsker类， 所以有(C1)。由估计函数生成的集合依然是一个P-G-C类，所以有(C2)。把文献[18]中引理4.1用于m(X，θ)， 得到(C3)。证毕。

我们定义

(6)

引理4 在条件1～5下，对θ-θ0=O(n-1/2)，有如下展开：

(7)

(8)

引理4的证明参看文献[17]中引理A.6。

定理1的证明 由条件3，E{m(X，θ)}=0有唯一的解θ0。由式(3)易得：

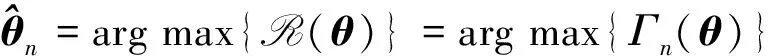
令

Γ(θ)=E{Γn(θ)}=-E[log{1+εT(θ)m(X，θ)}]，

其中ε(θ)满足

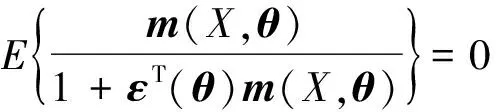
(9)

和

(10)

其中Dθ是包含θ0的闭区间。

事实上，由E{m(X，θ0)}=0得ε(θ0)=0，所以Γ(θ0)=0。在ε(θ0)处对ε进行Taylor展开得：

(11)

对某个α(θ)∈(0，ε(θ))。显然，式(11)小于零。结合Γ(θ0)=0即得式(10)。

对式(9)，我们令

Γn(θ)-Γ(θ)=Q1+Q2，

其中

Q2=-E[log{1+λn(θ)Tm(xi，θ)}]+E[log{1+ε(θ)Tm(xi，θ)}]。

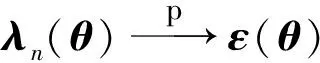
定理2的证明 由式(6)易得：

log{R(θ)}=nΓn(θ)。

(12)

由引理4得：

由条件5，当θ-θ0=O(n-1/2)，有：

log{p0(θ)}=log{p0(θ0)}+O(n-1/2)。

所以，

因为Jn是正定的，所以对任意的θ-θ0=O(n-1/2)，有：

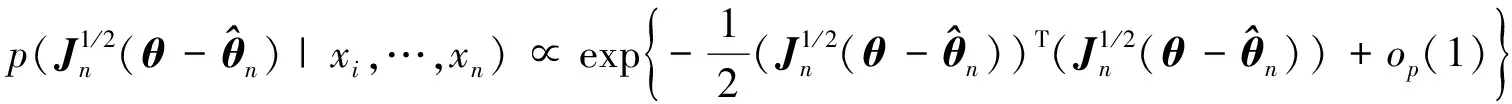
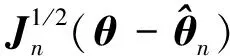
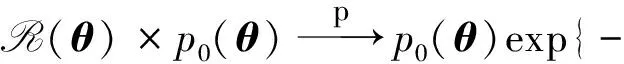
因为R(θ)×p0(θ)≤p0(θ)，由控制收敛定理，对任意δ≥0，有：

由此，当δ充分大时，对任意的ε>0有：

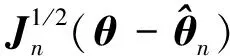
证毕。

[1] JORIAN P. Risk2: Measuring the risk in Value at Risk[J]. Financial Analysis Journal, 1996， 52(6):47-56. DOI:10.2469/faj.v52.n6.2039.

[2] ARTZNER P， DELBAEN F， EBER J M， et al. Thinking coherently[J]. Risk, 1997， 10: 68-71.

[3] ARTZNER P， DELBAEN F， EBER J M， et al. Coherent measures of risk[J]. Mathematical Finance, 1999， 9(3):203-228. DOI:10.1111/1467-9965.00068.

[4] ROCKAFELLAR R T, URYASEV S. Conditional Value-at-Risk for general loss distributions[J]. Journal of Banking and Finance， 2002， 26(7): 1443-1471. DOI:10.1016/S0378-4266(02)00271-6.

[5] PFLUG G C. Some remarks on the Value-at-Risk and the conditional Value-at-Risk[M]// URYASEV S. Probabilistic Constrained Optimization: Methodology and Applications. Dordrecht: Kluwer Academic Publisher， 2000: 272-281. DOI:10.1007/978-1-4757-3150-7_15.

[6] ACERBI C， TASCHE D. Expected shortfall: A natural coherent alternative to value at risk[J]. Economic Notes, 2002， 31(2):379-388. DOI:10.1111/1468-0300.00091.

[7] ACERBI C， TASCHE D. On the coherence of expected shortfall[J]. Journal of Banking and Finance, 2002， 26(7):1487-1503. DOI:10.1016/S0378-4266(02)00283-2.

[8] 晏振. VaR和ES的调整经验似然估计[D]. 桂林: 广西师范大学, 2012.

[9] OWEN A B. Empirical likelihood ratio confidence intervals for a single functional[J]. Biometrika, 1988，75(2): 237-249. DOI:10.1093/biomet/75.2.237.

[10] OWEN A B. Empirical likelihood[M]. London: Chapman and hall, 2001.

[11] QIN Jin, LAWLESS J. Empirical likelihood and general eatimating equations[J]. Annals of Statistics, 1994,22(1):300-325. DOI:10.1214/aos/1176325370.

[12] 张新成,张军舰,詹欢. 基于垂直密度表示的经验欧氏拟合优度检验[J]. 广西师范大学学报(自然科学版)，2013，31(4):60-65. DOI:10.16088/j.issn.1001-6600.2013.04.001.

[13] LAZAR N A. Bayesian empirical likelihood[J]. Biometrika, 2003， 90(2): 319-326. DOI:10.1093/biomet/90.2.319.

[14] YANG Yunwen, HE Xuming. Bayeian empirical likelihood for quantile regression[J]. The Annals of Statistics, 2012， 40(2):1102-1131. DOI:10.1214/12-AOS1005.

[15] RAO J N K, WU Changbao. Bayesian pseudo-empirical-likelihood intervals for complex surveys[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2010， 72(4):533-544. DOI:10.1111/j.1467-9868.2010.00747.x.

[16] Van der VAART A W. Asymptotic statistics[M]. Cambridge: Cambridge University Press， 1998.

[18] HE Xuming, SHAO Qiman. A general Bahadur representation ofM-estimators and its application to linear regression with nonstochastic designs[J]. The Annals of Statistics, 1996， 24(6):2608-2630. DOI:10.1214/aos/1032181172.

(责任编辑 黄 勇)

Bayesian Empirical Likelihood Estimation on VaR and ES

ZHANG Junjian, LAI Tingyu, YANG Xiaowei

(College of Mathematics and Statistics, Guangxi Normal University，Guilin Guangxi 541004, China)

VaR(value at risk) and ES(expected shortfall) are used to measure the loss of financial investment. It is interesting to investigate the estimation of VaR and ES. In this paper， VaR and ES are estimated by Baysian empirical likelihood method. Some properties，such as consistence and asymptotic normality，are given. Simulation studies show that，with some prior information，Baysian empirical likelihood is a better method.

value at risk; expected shortfall; Bayesian empirical likelihood

10.16088/j.issn.1001-6600.2016.04.006

2016-07-08

国家自然科学基金资助项目(11261009)；广西自然科学基金资助项目(2012GXNSFAA053004)；广西高等学校优秀中青年骨干教师培养工程资助项目；广西师范大学研究生创新基金资助项目(Ycsw2013058)

张军舰(1973—)，男，河南内乡人，广西师范大学教授，博士。E-mail:jjzhang@gxnu.edu.cn

O212.1

A

1001-6600(2016)04-0038-08