连续刚构桥风-浪作用效应分项系数确定方法*
2016-02-14陈忆前马如进陈艾荣彭伟
陈忆前 马如进 陈艾荣 彭伟
(1.同济大学 桥梁工程系, 上海 200092; 2.招商局重庆交通科研设计院有限公司, 重庆 400067)
连续刚构桥风-浪作用效应分项系数确定方法*
陈忆前1,2马如进1陈艾荣1彭伟2
(1.同济大学 桥梁工程系, 上海 200092; 2.招商局重庆交通科研设计院有限公司, 重庆 400067)
立足于海上多跨连续刚构桥,研究其在海上风-浪联合作用及不利的车辆布载影响下的可靠性能和设计表达式.从随机理论的角度出发,将作用于跨海连续刚构桥的汽车、风、浪作用简化为泊松过程,在采用Ferry Borges-Castanheta(简称FBC)法组合时进一步假设其为FBC过程.其中涉及的风、浪、车均为极端情况,风-浪作用组合时考虑两者的相关性,汽车作用的极端性体现在它的布置而非其荷载的大小上.为了确定极端风-浪作用影响下的跨海连续刚构桥设计表达式,采用思路步骤相对简单、主要依赖于计算机数据处理的Monte-Carlo方法进行模拟计算,根据结构可靠度指标与目标可靠度指标之差平方和为最小的原则,得出最佳设计分项系数.
可靠性分析;作用效应分项系数;风-浪耦合;极端作用;连续刚构桥
结构设计的总要求[1]是:结构的抗力R应大于或等于结构的综合作用效应S.由于实际中抗力和作用效应均为随机变量,R≥S并不能绝对满足,而只能在一定概率意义下满足,即
P{R≥S}=Pr=1-Pf
(1)
因此,结构设计更明确的要求是:在一定的可靠度Pr或失效概率Pf条件下进行结构设计,使得结构的抗力大于或等于结构的综合作用效应.
结构可靠性设计一般需要解决3个主要问题[2]:①结构的失效标准和失效模型;②确定结构的目标可靠指标;③推求设计表达式.
对跨海桥梁而言,需要其适应海上复杂而叵测的极端环境,目前尚没有针对此类状况进行过专门的设计.为了确定极端风-浪作用影响的极限状态设计表达式中的分项系数,需要考虑作用效应组合类型、构件种类、恒载、风浪车荷载、汽车荷载的运行状态和结构抗力的有关统计特征.
确定设计分项系数,实际上是结构可靠指标计算分析的逆运算.根据设计验算点法,将极限状态方程中的基本变量用各自的标准值和相应的分项系数代替,设计分项系数表达式为
(2)
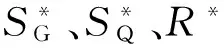
由上可知,设计分项系数γG、γQ、γR依赖于作用效应及抗力的设计验算点坐标,由结构可靠指标分析中得知,验算坐标与可靠指标有关,因而设计分项系数也与可靠指标有关.另外,验算点坐标和相应的可靠度指标均与可变作用效应与恒载效应的标准值之比值有关,这说明设计分项系数也与该比值有关.但在实际工程中,该值是变化的,这显然是不符合实用要求的.而最佳分项系数的取值应使采用该系数设计的结构所具有的可靠指标与规定的目标可靠指标之差为最小,也就是说,应该根据分项系数表达式求得的结构抗力标准值与按预先给定的目标可靠指标直接求得的结构抗力标准值之差为最小的原则来确定分项系数的取值.
1 风浪作用效应组合可靠性分析
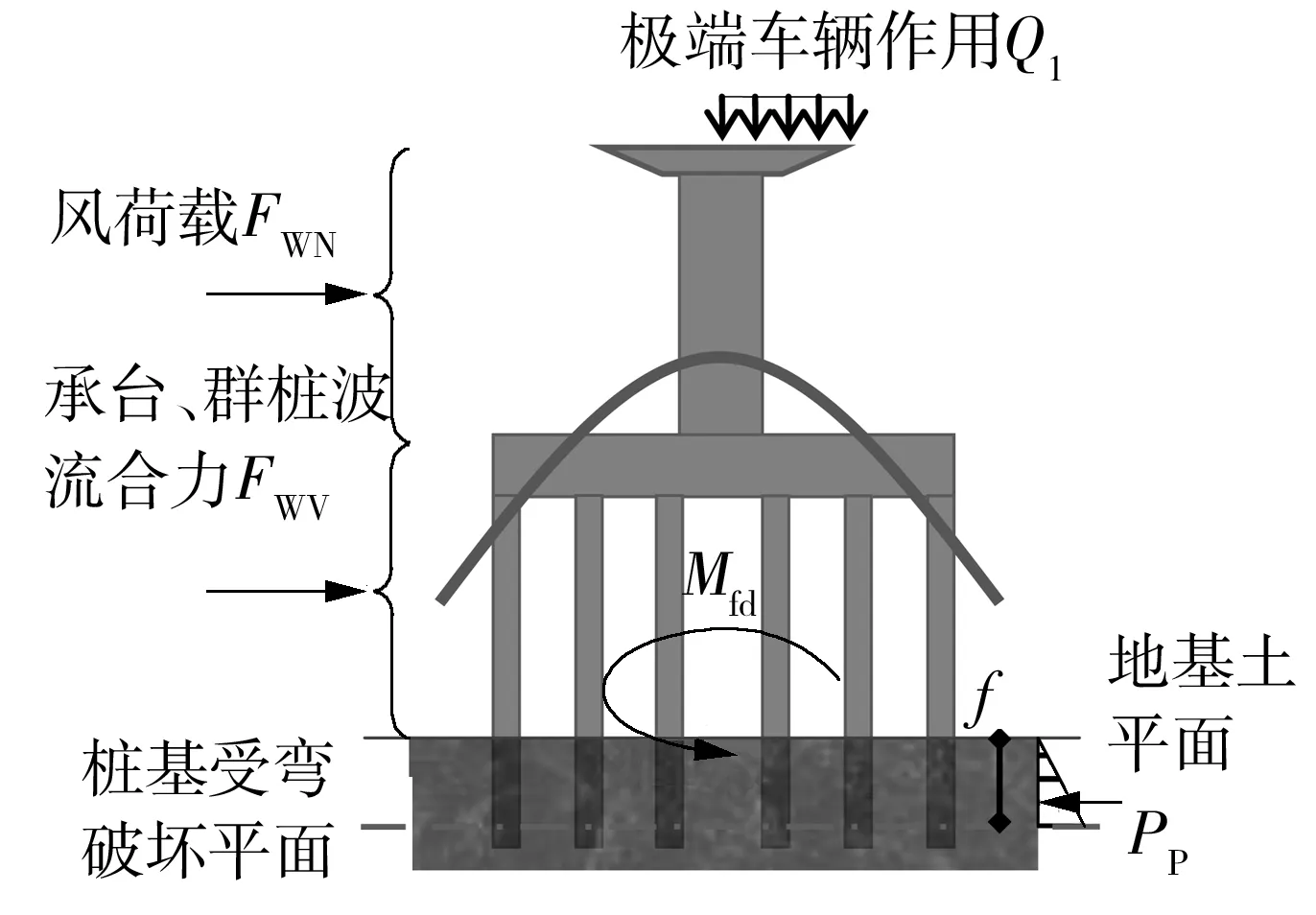
对于文中所针对的研究对象——连续刚构桥,墩梁固结传递弯矩,在横桥向风、浪、车3种荷载的作用下,主要有两种失效模式[3]:一是由于作为桩基础构件之一的桩柱受弯破坏而危及桥梁下部结构的安全,另外是由于地基土承载能力不足引起桩基础整体倾覆,其计算受力示意见图1(b)所示.
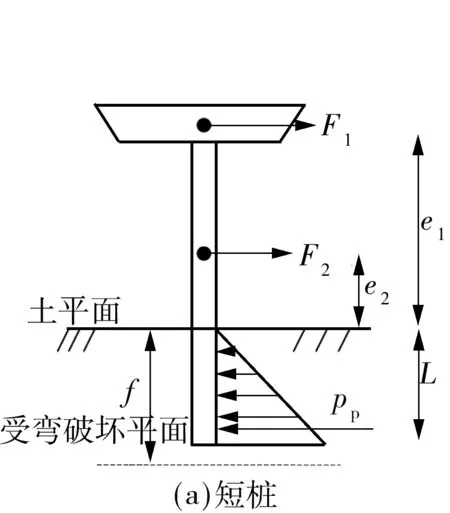


图1 桥梁结构受力示意图Fig.1 Stress diagram of bridge structures
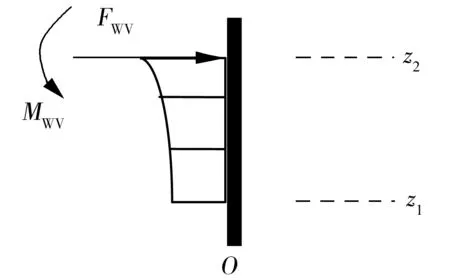
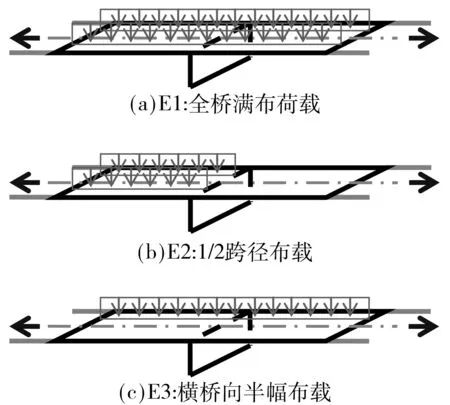
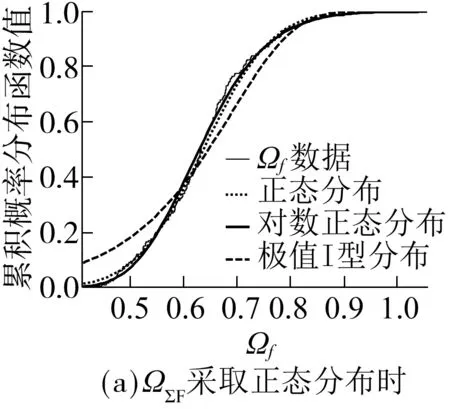
由图1(a)、(b)可知,若桩的破坏点距土平面距离f>桩基础埋深L,应视之为短桩,主要失效模式为桩基础整体的刚性倾覆,横向力F的力臂为L+e;若f 1.1 风荷载标准值FWNk 作用于主梁上的三向静阵风荷载如图1(c)所示,其标准值参考桥梁抗风规范[4]计算,除了一些按规定取值的参数外,主梁、桥墩的横向力(阻力)系数CH、主梁的竖向力(升力)系数CV、主梁的扭转力矩系数CM均通过风洞试验测定[5]或数值模拟方法计算. 某跨海连续刚构桥,地表类别为A类,基本风速值V10=43.3 m/s(设计基准期为100年).主梁横桥向水平静阵风荷载、扭转力矩标准值见表1,桥墩横桥向水平静阵风荷载标准值见表2,主梁纵桥向静阵风荷载标准值见表3,桥墩纵桥向水平静阵风荷载标准值见表4,其中,负号表示与图1(c)所示相反的方向. 表1 主梁横桥向水平静阵风荷载标准值 Table 1 Standard values of lateral horizontal static gust load for the main girder 节段号阻力系数CH节段平均投影高度Hi/m节段平均长度Li/m节段平均静阵风FH/kN0#-4#-2.22910.4853.167×2-532.0795#-11#-1.7797.9103.714×2-372.47112#-18#-1.7005.1344.357×2-271.14219#-24#-1.4063.6743.625×2-135.809合计——180-8240.998节段号扭转力矩系数CM主梁宽度B/m主梁长度Li/m主梁扭转力矩M/(MN·m)0#-4#-0.3035#-11#-0.17512#-18#-0.26419#-24#-0.216合计—17—38-11.93152-9.43061-16.68829-6.491180-44.540 表2 桥墩横桥向水平静阵风荷载标准值 Table 2 Standard values of lateral horizontal static gust load for the pier 随机变量标准值阻力系数CH-0.872迎风向投影面积An/m2137.6水平向静阵风FH/kN-408.047 表3 主梁纵桥向静阵风荷载标准值 Table 3 Standard values of longitudinal static gust load for the main girder 随机变量标准值水平向静阵风FH/kN-2060.249竖向静阵风FV/kN3108.589扭转力矩M/(kN·m)-11134.940 表4 桥墩纵桥向水平静阵风荷载标准值 Table 4 Standard values of longitudinal static gust load for the pier 随机变量标准值阻力系数CH-1.491迎风向投影面积An/m2309.6水平向静阵风FH/kN-1098.883 1.2 波流力标准值FWVk 对于连续刚构桥,作用在某一段桩z1-z2上的水平总波流力及对z1处波流力矩分别为[6] (3) 如果计入群桩效应,整个桩群上的总水平波流力为 (4) 根据式(3)和(4),可得到单桩水平波流力(矩)标准值FWVk(MWVk)和群桩波流力合力标准值∑FWVk,如图2所示.某跨海连续刚构桥整体桩基 础的波流合力∑FWV=∑Fp+Fc1+Fc2,其中∑Fp为桩柱水平波流(合)力,Fc1为下部承台水平波流力,Fc2为上部承台水平波流力,∑FWV标准值如表5所示. 图2 z1-z2段桩柱波流合力FWV及波流合力矩MWV Fig.2 Wave-flow forceFWVand momentMWVfor sectionz1-z2of a pile 表5 整体桩基础波流合力∑FWV标准值1)Table 5 Standard values of joint wave-flow force ∑FWV of the whole pile foundation 1)θ=kx-ωt,k为波数,m-1,x为距桩柱水平距离,t为时刻,ω为波浪的圆频,rad·Hz,θ取0~360°,以15°递增. 1.3 极端布置车辆作用标准值Q1k 对成桥结构来说,车辆荷载除了大小,其在桥梁结构上的布置亦有重大影响,尤其是对正承受极端作用的组合结构,对结构不利的分布可能产生“火上浇油”的效果.车辆在结构上的极端布置主要有3种情况,如图3所示. 图3 车辆极端布置示意图Fig.3 Diagram of vehicle extreme layouts 结合图1(b),Q1采用按E3布置的车道荷载,并计入汽车的冲击作用(汽车荷载标准值乘以冲击系数μ=0.05),可得其标准值为Q1k=4 583.25 kN. 1.4 风浪作用组合桩基础受弯破坏点距离f 根据朗肯被动土压力可得受弯破坏平面到土平面距离f仅与水平力相关.结构受横向风力及水平波流力的作用如图1、2所示,假设群桩中的每一根桩受力平均,f计算式如下: (5) 无量纲随机变量Ωf=随机变量f/fk,根据式(5),Ωf的概率统计特征值计算式如下: 均值 离散系数 (6) 式中,均值 离散系数 (7) 均值 (8) 离散系数 表6 Ωf统计特征值Table 6 Statistic characteristic values of Ωf 为了获知风浪车联合作用下Ωf的分布类型,根据式(6)采用Monte-Carlo方法.由于Ω∑F可能为正态或极值Ⅰ型任一种分布类型,模拟产生105个随机样本值,从中选取200个样本值. 若Ω∑F采取正态分布,最大偏差用正态分布拟合时为0.071 8,用对数正态分布拟合时为0.049 0;用极值Ⅰ型分布拟合时为0.129.取显著性水平α=0.05,相应临界值为0.095 2,如图4(a)所示,Ωf不拒绝服从正态分布及对数正态分布,但用对数正态分布拟合时更佳,因此选取对数正态分布作为Ωf的概率模型. 若Ω∑F采取极值Ⅰ型分布,最大偏差用正态分布拟合时为0.108,用对数正态分布拟合时为0.064 4;用极值Ⅰ型分布拟合时为0.254.取同一显著性水平,如图4(b)所示,Ωf不拒绝服从对数正态分布,选对数正态分布作为Ωf的概率模型. 综上所述,无论Ω∑F为正态分布还是极值Ⅰ型分布,Ωf都满足对数正态分布. 图4 受弯破坏点距离参数Ωf概率分布拟合 Fig.4 Probability distribution fitting for the distance parameterΩffrom the soil level to the point of maximum moment 1.5 桩基础抗弯承载力标准值Rk 对于拟建海上结构,按承载能力极限状态计算,应采用设计表达式[7]: R=γ0S (9) 式中,S为考虑风、浪、车三者作用的基本组合效应设计值,即 (10) 其中,由于永久作用不产生弯矩效应,风荷载弯矩效应超过汽车荷载弯矩效应.则风、浪、车组合作用下的构件抗弯承载力标准值可写为 Rk=Rd/γR Rd=γ0Sud= γ0(γWNSWVk+ψc(γWVSWVk+γQ1SQ1k))= γ0(SWVd+ψc(SWVd+SQ1d)) (11) 式中:γR为抗力分项系数,轴心受压构件γR=0.9,受弯、偏心受压、受拉和受扭构件γR=1.0[7],此处取γR=1.0;γWN为风荷载效应分项系数,按前文取γWN=1.4;γWV为波流荷载效应分项系数,按前文取γWV=1.4;γQ1为汽车荷载效应分项系数,按规范[8]取γQ1=1.4;ψc为在作用效应组合中除风作用效应外的其他可变作用效应的组合系数,根据规范[8]尚有两种其他可变作用时,取ψc=0.70. 1.6 可靠度校核 承载能力极限状态[9]直接关系到结构安全与否,任何桥梁工程结构均需做承载能力极限状态的设计,且要求其出现的失效概率相当低.文中基于结构构件或连接部因材料强度不够而破坏(包括疲劳破坏),或因过度变形而不适于继续承载这一失效状态来进行连续刚构桥的可靠性分析. 根据图5所示,连续刚构桥桩基础结构在成桥阶段的极限状态方程为 Z=R-S= (12) 图5 连续刚构桥下部结构受力示意图 Fig.5 Force diagram of substructure of continuous rigid frame bridge 要根据式(12)进行可靠度校核,还需要知道MWN+WV+Q1的概率统计特征值和发布类型.以下将对此进行探讨. (1)MWN+WV+Q1的概率统计特征值 根据FBC组合规则[10],有 (13) 式中,r1为在设计基准期100a内出现极端风的次数,r2为在极端风持续的4h内出现极端波流的次数,r3为在极端波流持续的2h内出现极端分布车辆E3的次数. 设风、浪、车组合效应的无量纲参数为 (14) 式中, ΩMWN= (15) ΩMWV=[Ω∑Fp(1+Ωfκ18)+ΩFc1(κ16+Ωfκ18)κ11+ ΩFc2(κ17+Ωfκ18)κ12-Ω∑Mpκ19-ΩMc1κ20- ΩMc2κ21]/[(1+κ18)+κ11(κ16+κ18)+ κ12(κ17+κ18)-κ19-κ20-κ21] (16) ΩMQ1=ΩQ1 (17) 式中,汽车荷载不定性ΩQ1的概率参数如下:均值μΩQ1=1.05,离散系数δΩQ1=0.1,满足正态分布[3]. (2)MWN+WV+Q1的概率分布类型 为了获知考虑极端风浪影响的可变作用弯矩效应组合ΩMWV+WV+Q1的分布类型,可参考1.4节相关内容,无论波流作用Ω∑FWV、ΩFc1、ΩFc2、Ω∑Mp、ΩMc1、ΩMc2选用正态分布还是极值Ⅰ型分布,风、浪、车极端组合弯矩效应ΩMWN+WV+Q1都满足对数正态分布,见图6. 图6 考虑极端风浪的可变作用组合弯矩效应ΩMWN+WV+Q1概率分布拟合 Fig.6 Probability distribution fitting for the moment effectΩMWN+WV+Q1under variable action combination consi-dering extreme wind-wave 由以上的分析得到了MWN+WV+Q1的概率统计特征值和发布类型,因此,针对某一连续刚构桥结构,按式(12)可校验其在考虑极端风浪影响的可变作用组合下的可靠度. 可靠指标过小会导致结构失效,过大又会使结构造价昂贵.基于可靠性的设计需要设计者首先确定以多大的失效概率作为设计目标,即目标可靠指标应选多大.目标可靠指标βT是结构设计的依据,是结构设计所要预期达到的指标[11]. 目标可靠指标的选择需要从结构失效后果、经济分析、过去经验、人类感知、政治决策等方面加以考虑.迄今为止许多学者都探讨了如何选择结构最优的目标可靠指标的问题.在冗余性及延性、构件及系统可靠度、新建及已建结构、重要及一般结构等领域都会涉及目标可靠指标. 为了确定文中考虑极端风浪作用影响的可变作用组合下跨海连续刚构桥的目标可靠指标βT,可利用现有国内外规范的目标可靠指标值,如表7所示. 对比上表各标准规范的βT取值可知,我国规范稍显保守.国外规范的取值是在安全措施的相对费用等级与失效后果等级两者之间所取得的平衡值,安全措施的相对费用低,意味着前期投入大建造成本高,结构不易失效.综合考虑各规范,在设计基准期T=100 a内的目标可靠指标按规范ACI 318[16]取值,即βT=4.5. 在考虑极端风-浪作用影响的情况下,对波流荷载而言,在进行墩柱式建筑物的强度和稳定性计算时,设计波浪的基准期应采用50年[17].因此,综合第1节中可靠度指标的分析,当M/Md=1.0时,β=2.0~3.2.根据这一计算结果,并参考文献[18]的研究成果,目标可靠度指标如表8所示,取较大的一组确定为跨海连续刚构桥桩基础墩柱的目标可靠度指标βT. 表7 国内外规范目标可靠指标βT1) Table 7 Target reliability indexβTin domestic and foreign specifications 中外规范安全措施的相对费用中等安全措施的相对费用低等失效后果中等失效后果严重失效后果中等失效后果严重我国规范[12]2)4.24.74.75.2ISO-2394[13]3)3.13.83.84.3JCSS[14]3)4.24.44.44.7AASHTO[15]4)3.55~6ACI318[16]3)3444.5 1)各国规范βT取值采用不同的划分标准;2)我国规范采用的标准分别为附加组合延性破坏构件、附加组合脆性破坏构件、主要组合延性破坏构件、主要组合脆性破坏构件;3)此3种规范采用的标准如表头所示;4)AASHTO采用的标准分别为钢筋预应力混凝土结构构件、结构系统. 表8 考虑极端风浪可变作用组合的目标可靠度指标βT Table 8 Target reliability indexβTfor variable action combination considering extreme wind-wave 组合方式波流作用服从正态分布的βT波流作用服从极值Ⅰ型分布的βT不考虑sys考虑sys不考虑sys考虑sys风-浪组合11)2.352.852.763.19风-浪组合22)2.042.592.502.96风、浪、车组合11)2.022.572.482.95风、浪、车组合22)2.062.602.512.97 1)波浪作用作为可变作用,作用效应分项系数为1.4;2)波浪作用作为偶然作用,作用效应分项系数为1.0. 3.1 分项系数确定原则 连续刚构桥结构风浪耦合作用设计分项系数的确定,主要考虑风、浪、车两相组合或3种全部组合的偶然情况[19],并遵循以下原则: (1)极端作用之一的分项系数取为1.0; (2)不同类型的构件取不同的抗力分项系数,但同一构件在同一组合下对不同运行状态取相同的抗力分项系数; (3)一组最佳的作用效应分项系数和抗力分项系数的取值,应保证采用该组合项系数设计的构件在不同的作用效应比值下的可靠指标β与目标可靠指标βT最为接近.即以极限状态设计表达式下的结构可靠度指标与目标可靠度指标误差最小的原则来确定分项系数,公式如下: (18) 式中,βTi为第i种构件的目标可靠度指标,βij为第i种构件在第j个风荷载作用效应与波浪作用效应的标准值比时,构件在极限状态设计表达式下的可靠度指标. 3.2 风浪作用效应组合分项系数的确定 对于不同形式(跨径、墩高、刚度等)的跨海连续刚构桥,在设计时,由于所考虑的作用效应设计值不同而抗力设计值不同,归根结底是作用效应的影响. 表9 4种工况下的可变作用效应分项系数 Table 9 Partial coefficients of variable action effects under four conditions 波流荷载分布类型sys影响风、浪、车作用效应分项系数ββTHi正态分布不考虑sys考虑sys极值Ⅰ型分布不考虑sys考虑sys综合推荐取值γWN=1.0γWV=1.9γQ1=1.4γWN=1.0γWV=1.9γQ1=1.5γWN=1.2γWV=1.5γQ1=1.2γWN=1.2γWV=1.5γQ1=1.1γWN=1.1γWV=1.7γQ1=1.32.042.062.97×10-22.602.601.65×10-22.522.510.91×10-22.992.970.87×10-2——— 为了验证作用效应分项系数推荐取值的合理性,采用该取值时4种工况下可靠度指标β随风、浪作用效应比κ变化的关系曲线如图8所示.由图可以看出,在4种工况下,可靠度指标β的变化曲线都较舒缓,说明风、浪作用效应的相对大小对可靠度指标的影响较小,即该作用效应分项系数推荐取值对不同形式的跨海连续刚构桥具有一定适用性. 图8 采用推荐作用效应分项系数时风、浪作用效应比、可靠度指标的变化曲线 Fig.8 Curves of effect ratio of wind action to wave action with reliability index from proposed partial factors of action effect 文中对某跨海连续刚构桥在风-浪作用影响下的可靠性进行了校核,包括根据现行设计规范计算各作用效应的标准值、各作用下结构构件抗力标准值和相应极限状态方程下的可靠度指标.参考国内外相关标准,结合校核法计算所得的可靠度指标,确定了连续刚构桥在风、浪、车组合作用下的目标可靠度指标βT,并以此计算出风+浪+车的作用效应分项系数:γWN=1.1,γWV=1.7,γQ1=1.3,最终确定极端风-浪作用影响的连续刚构桥的设计表达式,即 式中,当极端浪或汽车作用在效应组合中的值超过风荷载效应时,则该作用取代风荷载,其分项系数应采用风荷载的分项系数. 由于只考虑了风、浪、车3种极端作用及其组合,对跨海连续刚构桥而言还不够完善,但至少以这种跨径相对较小、结构形式相对简单的跨海桥型为始,对其极端作用下的设计搭建了一个框架,在此基础上可以进行更多细致且拓展性的工作. [1] 李国强,黄宏伟,吴迅,等.工程结构荷载与可靠度设计原理 [M].3版.北京:中国建筑工业出版社,2005. [2] 张建仁.结构可靠度理论及其在桥梁工程中的应用 [M].北京:人民交通出版社,2003. [3] GHOSN M,MOSES F,WANG J.Design of highway bridges for extreme events [R].Washington D C:Transportation Research Board,2003. [4] JTG/T D60-01—2004:公路桥梁抗风设计规范 [S]. [5] 陈艾荣,马如进,王达磊,等.强台风作用下跨海连续刚构桥(平潭海峡大桥)长悬臂施工安全研究 [R].上海:同济大学桥梁设计方法与过程研究室,2010. [6] 陈忆前.跨海连续刚构桥风-浪耦合作用设计方法研究 [D].上海:同济大学土木工程学院,2013. [7] JTG D62—2004:公路钢筋混凝土及预应力混凝土桥涵设计规范 [S]. [8] JTG D60—2004:公路桥涵设计通用规范 [S]. [9] 杜尚泽.可靠度理论在桥梁中的应用 [J].中国水运(理论版),2006,4(4):84- 85. DU Sang-zhe.Application of reliability theory in Bridge [J].China Water Transport(Theory Edition),2006,4(4):84- 85. [10] BORGES J F.Structural safety [M].Lisboa:Laboratório Nacional de Engenharia Civil,1971. [11] 李扬海,鲍卫刚,郭修武.公路桥梁结构可靠度与概率极限状态设计 [M].北京:人民交通出版社,1997. [12] GB/T 50283—1999:公路工程结构可靠度设计统一标准 [S]. [13] ISO 2394:1998(E):Norme Internationale ISO 2394 [S]. [14] JCSS:Probabilistic model code,Part 1—Basis of design [S]. [15] AASHTO.AASHTO LRFD bridge design specifications:customary U.S.Units [M].3 ed.Washington D C:American Association of State Highway and Transportation Officials,2005. [16] ACI:Building Code Requirements for Structural Concrete (ACI 318—08) and Commentary [S]. [17] JTJ 213—98:海港水文规范 [S]. [18] 沈照伟.基于可靠度的海洋工程随机荷载组合及设计方法研究 [D].杭州:浙江大学建筑工程学院,2004. [19] BOSAK G,FLAGA A.Probabilistic and deterministic aspects of combinations of wind,thermal and dead loads on cooling towers [J].Journal of Wind Engineering and Industrial Aerodynamics,1996,65(1/2/3):107- 200. A Method to Determine Partial Safety Factors for Continuous Rigid Frame Bridges under Wind-Wave Effect CHENYi-qian1,2MARu-jin1CHENAi-rong1PENGWei2 (1.Department of Bridge Engineering, Tongji University, Shanghai 200092, China; 2.China Merchants Chongqing Communications Technology Research and Design Institute Co., Ltd., Chongqing 400067, China) In this paper, the reliable performance and design expression of a cross-sea multi-span continuous rigid frame bridge are investigated under the combined effect of the wind-wave and the adverse effect of the vehicle. Then, based on the stochastic theory, the vehicle, wind and wave actions on the cross-sea continuous rigid frame bridge are simplified as a Poisson process, and are further assumed as a FBC process when the Ferry Borges-Castanheta (FBC) method is adopted. All the wind, wave and vehicle actions are considered to be in extreme cases, and when the wind and wave actions are combined, their correlation is also taken into account. Moreover, the extreme nature of the vehicle is reflected in the load layout rather than in the load value. In order to determine the design expression of the cross-sea continuous rigid frame bridge under the extreme wind-wave effect, the Monte-Carlo method, which is simple and mainly dependent on the computer data processing, is adopted to perform a simulation. Finally, according to the principle of keeping the sum of the squares of the differences between the structural reliability indexes and the target reliability indexes to a minimum, the optimal design partial safety factor is obtained.Key words:reliability analysis; partial safety factor of an action effect; wind-wave coupling; extreme action; continuous rigid frame bridge 2015- 10- 13 国家科技支撑计划项目(2014BAB16B05) Foundation item: Supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China(2014BAB16B05) 陈忆前(1980-),女,博士生,主要从事桥梁结构理论、极端作用组合设计方法研究.E-mail:yiqianch@126.com 1000- 565X(2016)12- 0104- 08 U 441+.2 10.3969/j.issn.1000-565X.2016.12.015





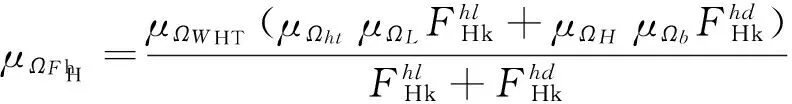





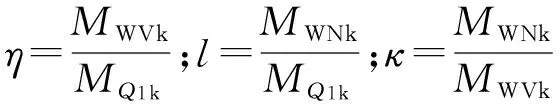
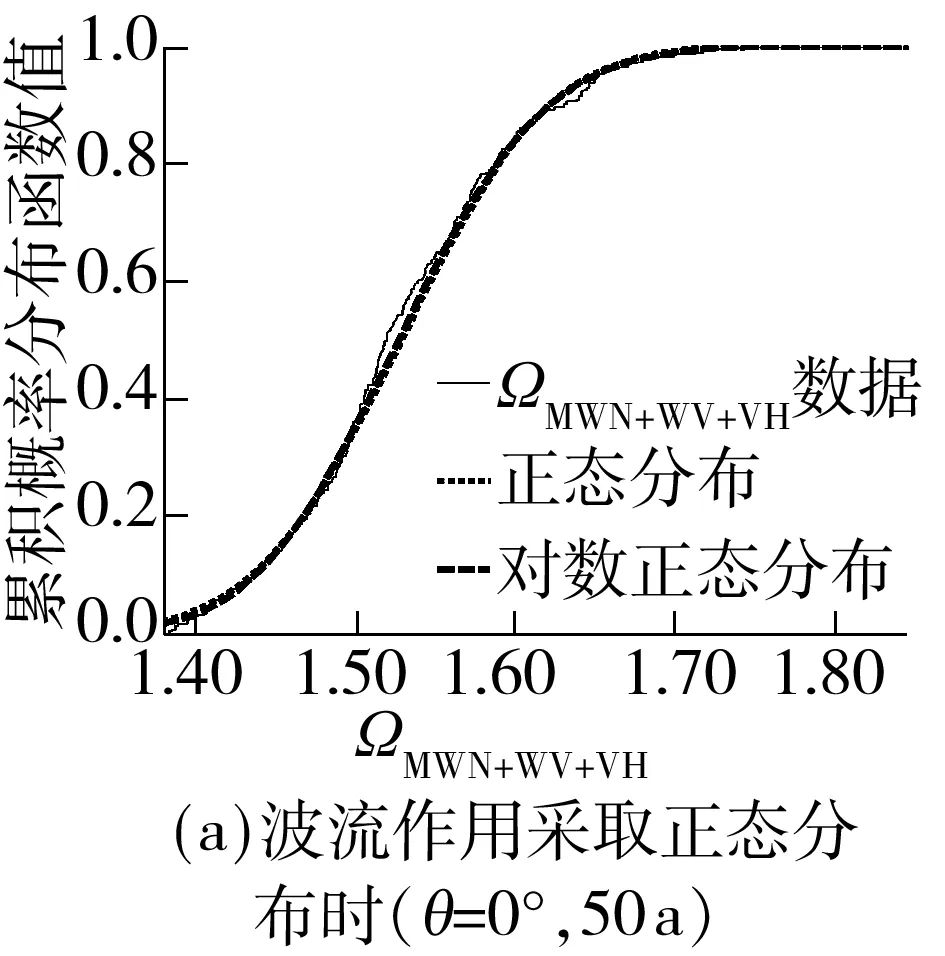
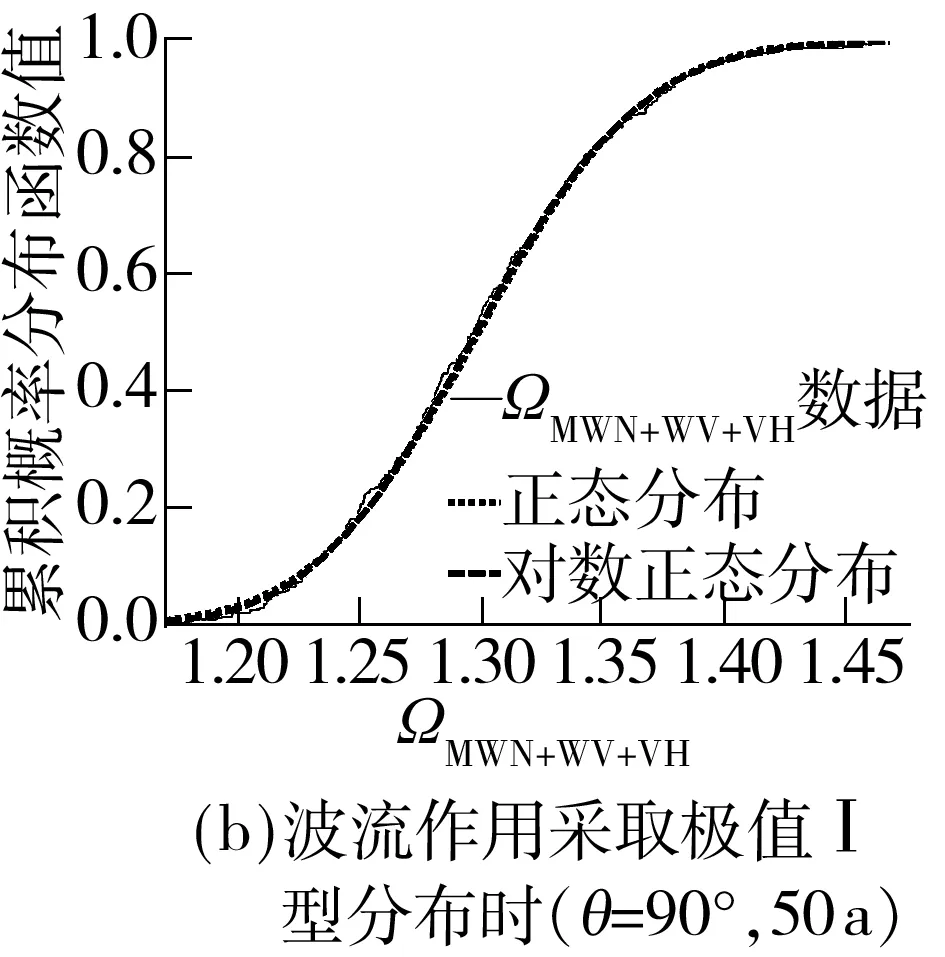
2 目标可靠指标的确定

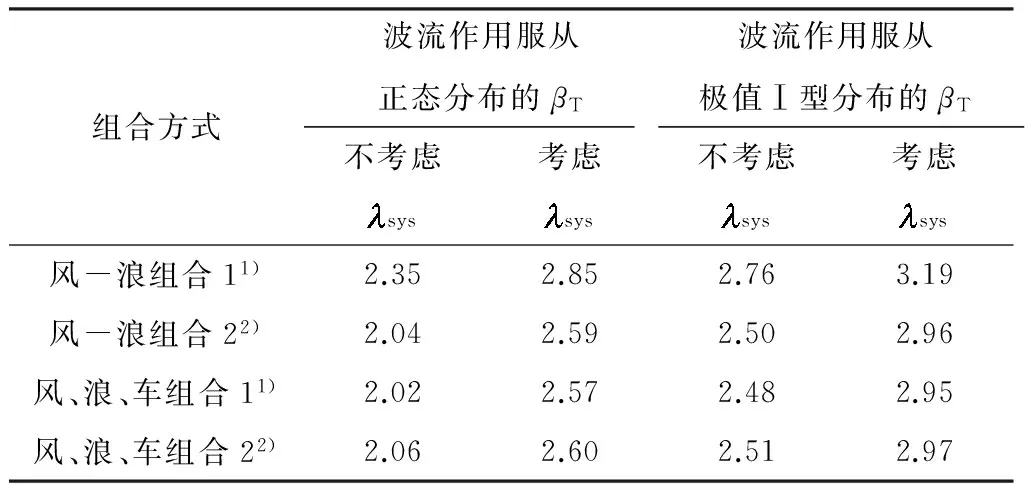
3 风浪作用效应组合设计分项系数




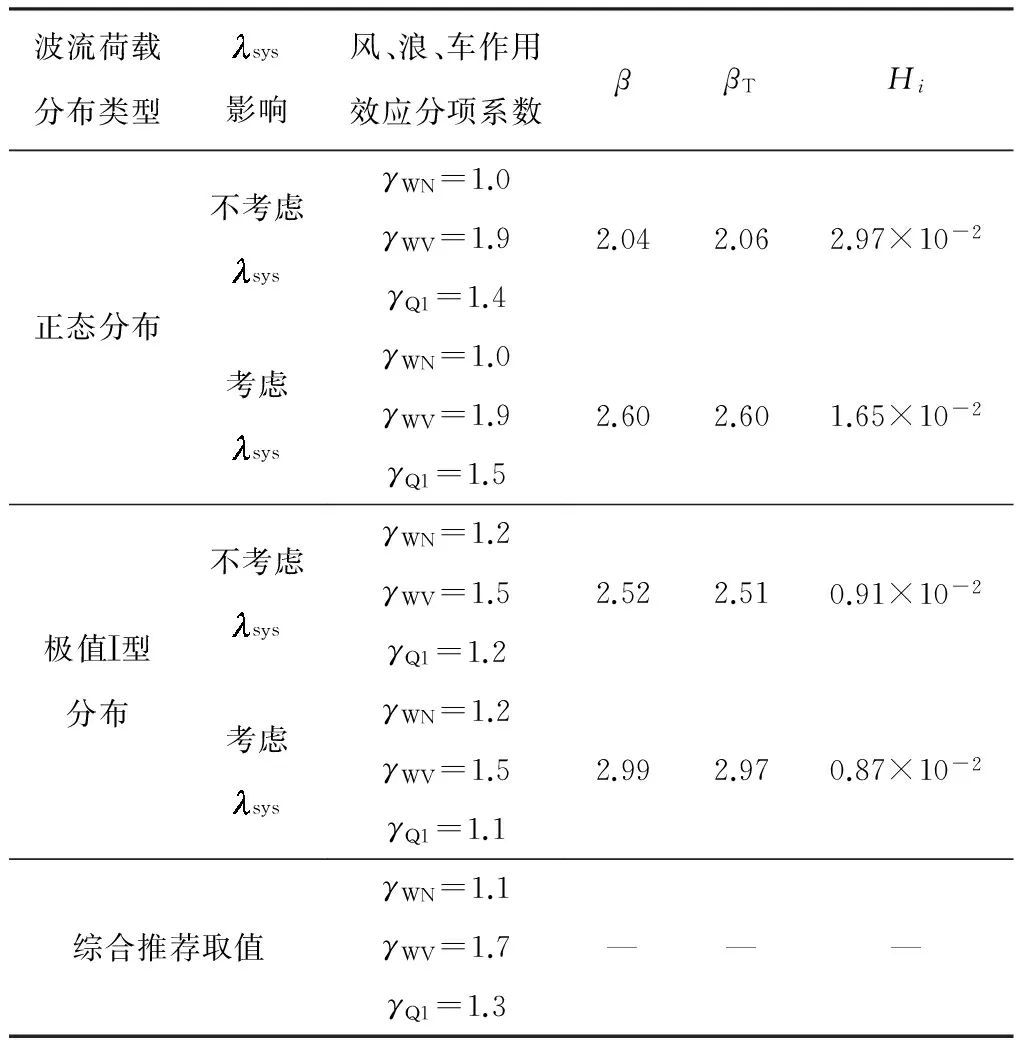
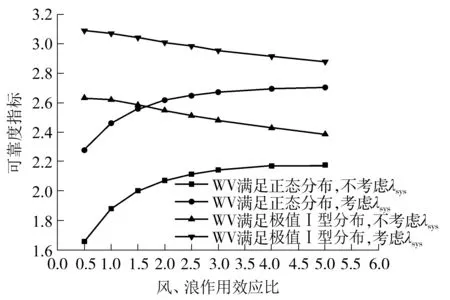
4 设计表达式的确定

5 结语
