三维带分数阶耗散不可压Maxwell-Naiver-Stokes方程组解的全局存在性
2016-02-10李卫文赵文波孙小科浙江师范大学数理与工程信息学院浙江金华3004天水师范学院电子信息与电气工程学院数学与统计学院甘肃天水7400
李卫文,赵文波,孙小科(.浙江师范大学 数理与工程信息学院,浙江 金华 3004;.天水师范学院 电子信息与电气工程学院,数学与统计学院,甘肃 天水 7400)
自然科学研究
三维带分数阶耗散不可压Maxwell-Naiver-Stokes方程组解的全局存在性
李卫文1,赵文波2,孙小科2
(1.浙江师范大学 数理与工程信息学院,浙江 金华 321004;2.天水师范学院 电子信息与电气工程学院,数学与统计学院,甘肃 天水 741001)
研究三维带分数阶耗散不可压Maxwell-Naiver-Stokes方程组,当α>3时,利用能量方法得到2了该方程组解的全局存在性结果.
Maxwell-Naiver-Stokes方程组;全局存在性
引言
考虑如下三维不可压Maxwell-Navier-Stokes方程组:
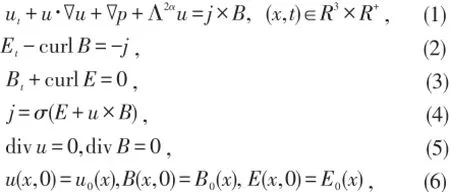
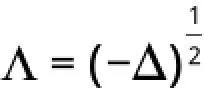
Naiver-Stokes方程刻画了粘性流体运动的基本力学规律,在流体力学中有着十分重要的意义.而Maxwell方程和Lorentz方程是经典电磁学基础方程,从这些方程的相关理论中发展出了现代电子、电力科技,因此研究这些方程具有重要的理论意义和应用前景.
目前,经典的Maxwell-Navier-Stokes(α=1)方程组已经得到了广泛的研究.在二维的情形下,Mas⁃moudi等人在文献[2],[3]中分别证明了当初值
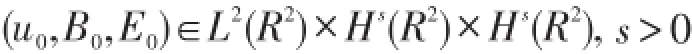
以及
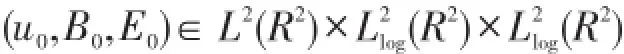
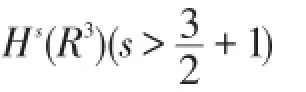
当忽略位移电流Et的影响时,Maxwell-Navier-Stokes方程组可化MHD[6]方程组,而对于MHD方程组已经有了大量的研究成果,例如解的唯一性、[7]爆破性准则、[8]大时间行为以及粘性消失极限[9]等.但是对于Maxwell-Navier-Stokes方程组与MHD方程组的结构而言,两者之间有着很大的不同,因此研究这些问题需要更多的技巧与方法.
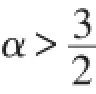
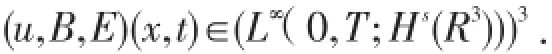
1 基本引理
为了证明定理1,通过Picard定理及先验估计可以得到如下引理:
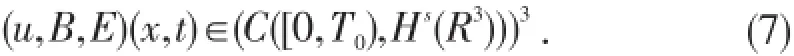
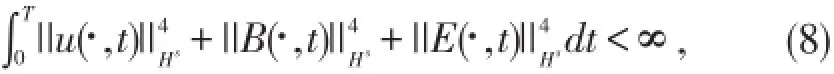
引理 3[10](Moser型不等式)f∈Ws,q2,Λf∈Lp1,,则有其中1<p<∞,p1,p2∈(1,∞],s>0且
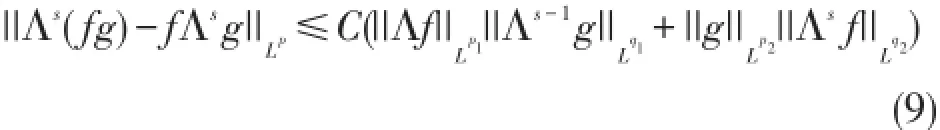
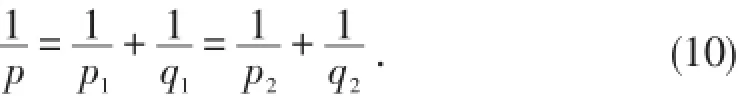
2 定理1证明
首先,在(1)-(3)分别乘以u,B,E,并关于x积分然后将结果相加,得到基本能量估计
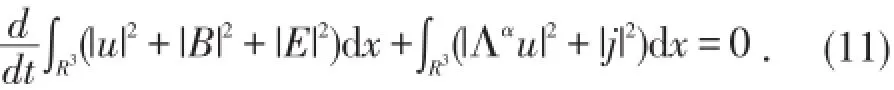
这表明 u∈L∞(0,T;L2)⋂L2(0,T;Hα),(B,E)∈L∞(0,T;L2)和 j∈L2(0,T;L2).
在(1)~(3)两边作用算子Λ,对其分别乘以Λu,ΛB,ΛE,并关于x积分然后将其相加,得到
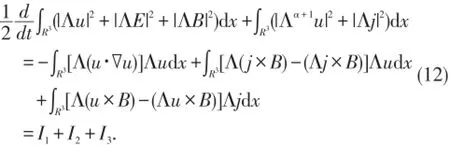
现在给出 Ii,i=1,2,3的估计.对于 I1利用Hölder不等式、Young不等式和Gagliardo-Nirenberg不等式,有
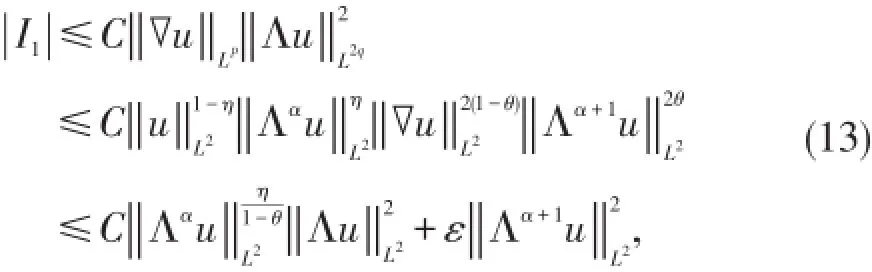
对于I2,运用Moser型不等式、Hölder不等式、Young不等式和Gagliardo-Nirenberg不等式,得到
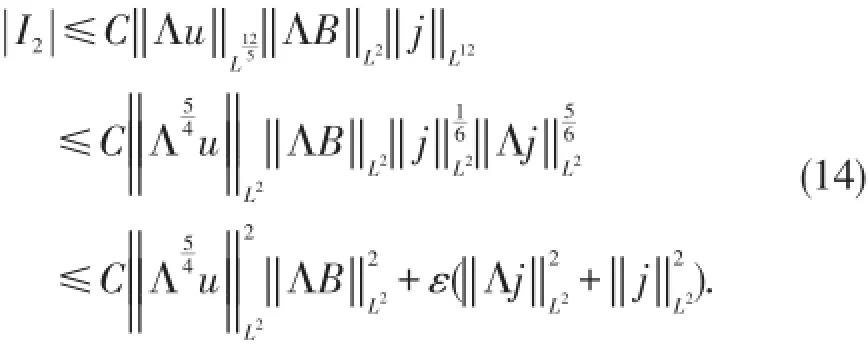
同样,对于I3
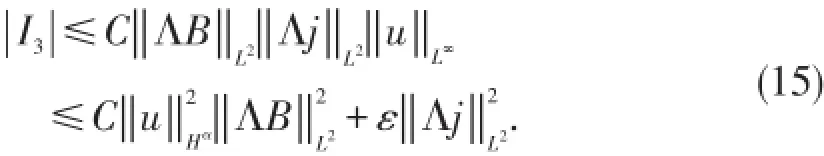
将(13)~(15)代入(12)并与(11)相加,然后应用Gron⁃wall不等式,得到
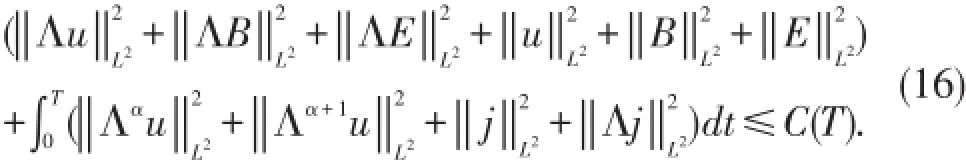
接下来进行二阶估计,先在(1)~(3)式两边作用算子Λ2,然后对其分别乘以Λ2u,Λ2B,Λ2E,并关于x积分然后相加,得到
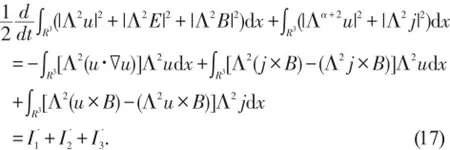
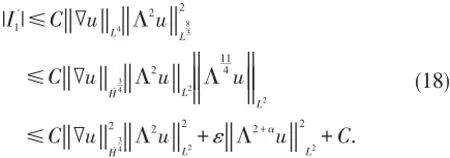
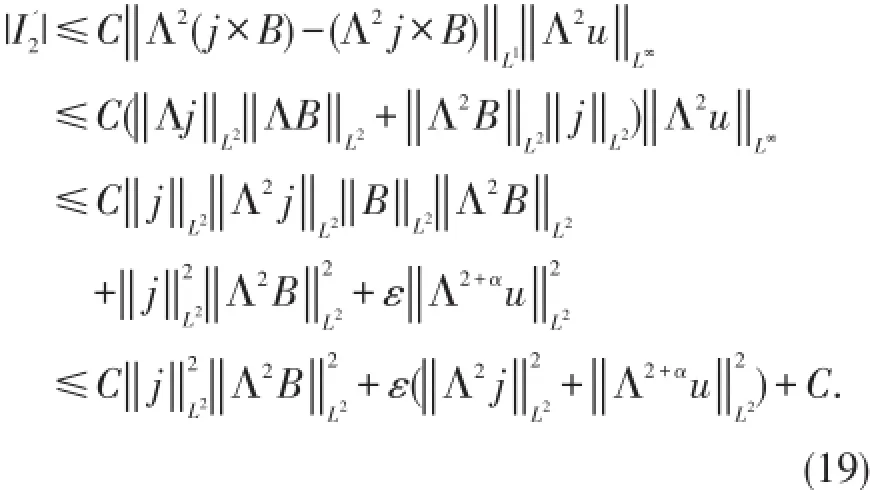
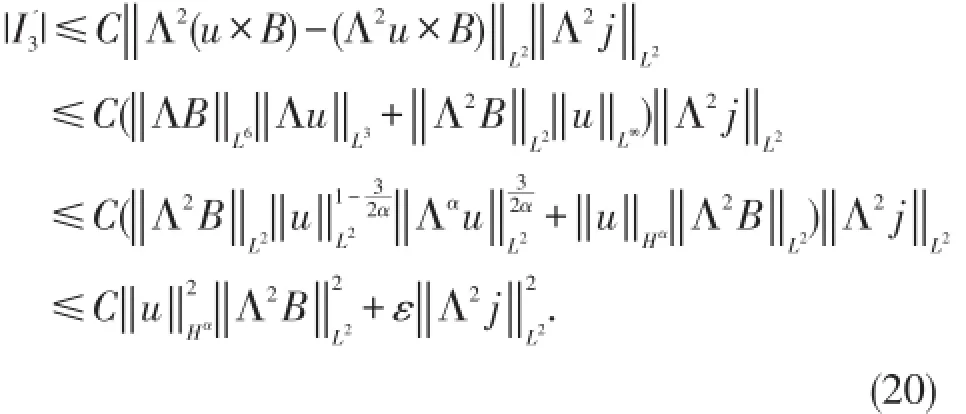
将(18)~(20)代入(17)并结合(11),应用Gronwall不等式,得到
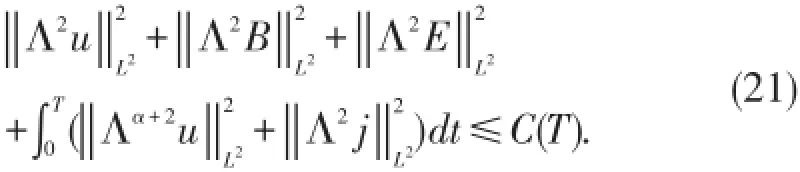
至此,结合引理2我们完成了定理1的证明.
[1]CHEMIN J.Y..Perfect incompressible fluids[M].England:Clarendon press.Oxford,1998.
[2]MASMOUDI N..Global well posedness for the Maxwell-Na vier-Stokes system in 2D[J].Pures Et.Appl.2010,93:559-571.
[3]GERMAIN P.,IBRAHIM S.,MASMOUDI N.On the wellposedness of the Navier-Stokes-Maxwell system[J].Proc.Roy.Soc.Edinburgh Sect.A,2012,144(1):71-86.
[4]FAN J.,Li F..Uniform Local well-posedness to the Density-Dependent Navier-Stoke-Maxwell system[J].Acta Appl.Math,2014,133:19-32.
[5]IBRAHIM S.,KERAANI S..Global small solutions for the Navier-Stokes-Maxwell system[J].SIAM J.Math.Anal,2011,43:2275-2295.
[6]BISKAMP D..Nonlinear Magnetohydrodynamics[M].England:Cambridge University Press.Cambridge,1993.
[7]SERMANGE M.,TEMAM R..Some mathematical questions related to the MHD equations[J].Comm.Pure Appl.Math,1983,36(5):635-664.
[8]LEI Z.,ZHOU Y..BKM's Criterion and global weak Solu tions for magnetohydro-dynamics with zero viscosity[J].Dis⁃crete Contin.Dyn.Syst,2009,25(2):575-583.
[9]DíAZ J.I.,LERENA M.B..On the inviscid and non-resistive limit for the equations of incompressible magnetohydrody namics.Math[J].Models Methods Appl.Sci,2002,12(10):1401 -1419.
[10]KLAINERMAN S.,MAJDA A.J.Singular limits of quasilin ear hyperbolic systems with large parameters and the incom⁃pressible limit of compressible fluids[J].Comm.Pure Appl.Math,1981,34:481-524.
〔责任编辑 高忠社〕
Global Existence of the Solution to the Three Dimensional Incompressible Maxwell-Navier-StokesEquations with Fractional Dissipation
Li Weiwen1,Zhao Wenbo2,Sun Xiaoke2
(1.College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua Zhejiang321004,China;2.School of Electronic Information and Electrical Engineering,Tianshui Normal University,Tianshui Gansu741001,China)
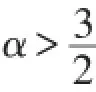
Maxwell-Navier-Stokes equations;global existenc
O175.27
A
1671-1351(2016)02-0001-03
2016-01-21
李卫文(1992-),女,浙江嘉兴人,浙江师范大学数理与工程信息学院在读硕士研究生。
甘肃省高等学校科研项目(2015A-131)及天水师范学院校列项目(TSA1406)阶段性成果
