铁路客车上水单元机软管缠绕水头损失分析

侯世全，洪蔚

(中国铁道科学研究院节能环保劳卫研究所，北京 100081)

环境保护

铁路客车上水单元机软管缠绕水头损失分析

侯世全，洪蔚

(中国铁道科学研究院节能环保劳卫研究所，北京 100081)

本文首先对单个弯管的转弯半径与管径之比值对局部水头损失阻力系数的影响进行了分析；在对相关技术文献调研的基础上，认为消防水带蜿蜒铺设上水较符合铁路客车上水单元机水管缠绕上水的情况，其局部水头损失计算方法综合考虑了转弯半径与管径之比值和上水管大角度转弯的影响。根据上水单元机水管多圈连续缠绕情况，研究提出了铁路客车上水单元机水管缠绕上水附加水头损失计算公式。在上水单元机上进行了验证试验，结果表明所提出的计算方法可行。

铁路客车上水；水管弯曲；动水压力；水头损失

近年来，铁路客车上水单元机得到了广泛的应用。各种上水单元机均配备了卷筒和上水软管，上水软管缠绕在卷筒上，上水时人工将软管从卷筒上拉出，上水作业完成后，软管自动被回收缠绕在卷筒上。该类单元机的应用具有减少上水软管接头的污染、降低现场作业员工的劳动强度、保持股道间场地整洁的作用，但软管在卷筒上缠绕上水会带来附加的水头损失，进而造成上水流量减少，使得上水作业时间加长[1]，不适应当前车站作业整备时间越来越短的要求，因此有必要对这种因上水管缠绕引起的附加的水头损失进行分析计算。

按照常用的水头损失计算方法，上水系统的水头损失是由沿程水头损失和局部水头损失之和组成，对上水单元机系统而言，沿程水头损失可采用传统方法计算，但因确定不了局部损失系数而无法计算水管缠绕造成的局部水头损失，也因为目前关于水管在卷筒上缠绕的水力学分析研究较少，尚无法定量地计算上水单元的上水流量，使得上水单元给水设计存在困难。

本文根据上水单元机上水作业时软管的缠绕状况，收集并分析了相关技术文献的研究成果，提出了适合铁路客车上水单元机情况的软管缠绕的水头损失计算方法，并和试验结果进行了比较，为铁路客车上水单元机的水力计算提供了参考依据。

1 弯管局部水头损失

弯管内流动的流体在离心力作用下，管道外壁面处压力增加，内壁面处压力减小，管中心处的速度最大，离心力作用也比壁面处大，因此流体在断面内受力不平衡，在过流断面上形成二次流，二次流与轴向流动耦合产生了双螺旋流，进而产生了弯管的局部水头损失，90°直角弯管的阻力损失系数见表1。

表1 90°直角弯管的阻力损失系数[2]

rd1246ζ0 350 190 160 21

注：r为管中心处的转弯半径，d为管径。

2 水带蜿蜒铺设时局部水头损失

文献[3]探讨了消防水带蜿蜒铺设时的水头损失，认为总水头损失是直线敷设的沿程水头损失和因水带弯曲产生的局部水头损失之和。沿程水头损失可按常规办法计算，因水带弯曲产生的局部水头损失可按下式计算：

(1)

式中：

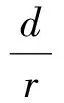
3 上水单元机软管缠绕水头损失

综合以上分析，提出铁路客车上水单元机软管缠绕水头损失计算公式：

h=hf+hj

(2)

式中：

h为上水单元机软管缠绕上水总水头损失，m；

hf为软管全部拉直上水时的水头损失，m；

hj为软管部分或全部缠绕产生的附加水头损失，m。

公式(2)中，hf可按常规水头损失公式计算，包括全部管路沿程损失和因电磁阀、旋转接头、快速接头等引起的局部水头损失之和。

附加水头损失由下式计算：

(3)

式中：

n为软管缠绕圈数，无量纲；

其余符号意义同前。

软管在卷筒上的缠绕圈数是由软管外径、管长、卷筒半径及轮缘间距决定的。一般上水软管内径为25 mm，外径35 mm左右，长度一般为15 m，按软管有序缠绕估算转弯圈数。在设计时，应按软管全部缠绕在卷筒上计算。若实际作业，软管可能仅部分缠绕在卷筒上，水头损失较设计值偏小。

4 上水试验

在我单位生产的上水单元机上进行了上水验证试验。

上水单元机为电动卷筒，卷筒最小直径250 mm，两轮缘间距190 mm，DN25软管长度15 m，外径35 mm。 软管在卷筒上基本为有序缠绕，软管被完全回收后在卷筒上缠绕15圈。试验时将上水单元机水平搁置在地面上，出水管口和进水管口高程一致，分别测出软管被完全回收后在卷筒上缠绕和软管被完全拉出且不弯曲搁置两种情况下的出水流量，比较分析水管缠绕的附加水头损失。

在软管全部拉直状态下，对进出水管口列伯努利方程：

(4)

式中：

p为动水压强，Pa；

γ为水容重,N/m3；

λ为沿程摩阻系数，无量钢；

ζi为局部摩阻系数，无量钢。

在软管全部缠绕在卷筒上的状态下，对进出水管口列伯努利方程：

(5)

公式(5)-公式(4)可得：

(6)

在试验范围内，因拉直状态和缠绕状态雷诺数变化不大，可近似认为λ1=λ2，故公式(6)可改写为：

(7)

根据试验数据，拉直状态下，动水压p1为22 m，流速ν1为3.67 m/s，代入公式(4)中，求得：

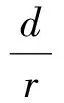
(8)

缠绕状态下，动水压p2为24.2 m，流速ν2为3.46 m/s，n为15，代入公式(8)中，

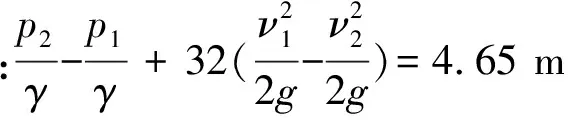
可见公式左右两侧相差无几。说明本文推荐的缠绕状态下的水头损失计算公式是可行的。

5 结论

(3)提出软管缠绕的水头损失计算公式，其沿程水头损失用常规方法计算；软管缠绕附加水头损失采用水带蜿蜒铺设的局部水头损失公式计算。其弯曲角度采用在卷筒上缠绕的圈数乘以360°。

(4)在上水单元机上进行的软管全部拉伸和全部缠绕的上水对照试验数据表明，本文提出的上水软管缠绕状态下的水头损失计算公式是可行的。

[1] 侯世全，洪蔚．铁路客车上水流量影响因素探讨[J]．铁路节能环保与安全卫生，2015，5(4)：152-156.

[2] 赵孝保，周欣．工程流体力学[M]．南京：东南大学出版社，2008：128．

[3] 王玉．水带蜿蜒铺设时水头损失估算及火场供水研究[J]．防灾科技学院学报，2011，13(4)：45-47.

A Study on the Head Lose of Winding Hose of Railway Watersupply Equipment

HOU Shiquan, HONG Wei

(EnergySaving&EnvironmentalProtection&OccupationalSafetyandHealthResearchInstitute,ChinaAcademyofRailwaySciences,Beijing100081,China)

On the basis of analysis on the local head loss of curved tube and bendy fire hose, the computational equation for the additional head loss of railway watersupply equipment’s winding hose was proposed, and was proved feasible throgh water supply test.

railway watersupply equipment; winding hose; hydrodynamic pressure; head lose

2015-11-25；

2016-01-08

侯世全(1951—)，男，河南辉县人，研究员，从事节能环保、给排水工作。

2095-1671(2016)01-0001-04

U291.1+<8 class="emphasis_bold">8 文献标志码：B8

B