基于多元回归分析的血氧含量检测方法的研究

金益波，王勤美

温州医科大学，温州市，325027

基于多元回归分析的血氧含量检测方法的研究

【作者】金益波，王勤美

温州医科大学，温州市，325027

在传统的血氧检测中，使用修正的朗伯-比尔定律对血氧进行计算，一方面计算过程中需要进行除法等运算，不利于硬件快速输出结果。另一方面，这种方法因使用了比值的方法会带来计算误差，损失了一定的信息量，在输出结果上使最后的计算精度较低。为减小这种情况影响，该文提出了回归分析的方法对血氧含量进行测量和评估，相比原有的比值法计算血氧饱和度，测量的精度有着明显的优势，同时更利于硬件实现。

血氧检测；多元回归分析

0 引言

氧是一切生命活动的基础，是生命活动最为重要的物质之一。生命的一切活动和代谢等均需要氧气的参与，一旦组织细胞供氧量不够，几分钟内，细胞就会开始死亡，严重时会危及组织乃至生命[1-3]。因此，血氧检测是医学常规检测中比较重要的一个项目。

通常对血氧的检测有两种方式，分别为有创检测和无创检测。有创检测不仅需要有效的样本采集，而且要求样本在检测过程中不受污染。同时有创检测不但存在不能实时检测的缺点，而且会对被检测者造成痛苦。因此有创检测不适合应用在日常生活中以及病患体征监测等方面。

血氧的无创检测是当前流行的血氧检测技术，通常都是利用近红外光谱对待测部位进行光照透射，完成对血氧的检测。其检测结果受检测部位、内部体脂含量、体内组织分布和结构等因素影响[4]。为解决这些问题，通常近红外血氧无创检测使用朗伯—比尔修正定律对结果进行校正，这使检测结果精度有了提高。然而人体组织的复杂性导致修正的朗伯—比尔定律计算结果依旧与实际存在偏差。这是因为实际中的朗伯—比尔定律中的常数计算项并非是一个稳定的常数，而是与血氧饱和度等因素相关的函数。

本文提出了利用多元回归分析的方法对血氧含量进行测量及评估，相比单纯使用朗伯-比尔修正定律，这种方法可以使测量精度进一步提高。

1 检测原理

所谓的朗伯—比尔定律（Lambert-Beer Law）是组织光学中所依据的最重要的定律之一，其定义了波长为λ的光线在组织行进中的变化情况。经典的郎伯—比尔定律通过对组织厚度和单色光的吸收程度进行描述来分析光路上强度的变化，其构成分为郎伯定律和比尔定律。所谓的郎伯—比尔定律就是将两者公式进行结合，得到一个同时对溶液浓度和光路方向上液体厚度考量的公式，如式(1)所示：

其中，OD表示液体的吸光度，是关于入射光频率的函数，I0是入射光的强度，I1是出射光的强度，εn为对应溶液某成分的吸光系数，L为光路方向上介质厚度，Cn为对应的溶液某成分的浓度[5-7]。

然而在实际生物组织中，光线的行进并不是按理想状态前行，需要同时考虑组织对光线的吸收和散射作用。而且实际的组织也并不是纯溶液介质，因此郎伯—比尔定律并不能完全反映这种现象。根据这个问题，Delpy等在1988年提出了郎伯—比尔定律的改进方法，修正后的郎伯—比尔方程如式(2)所示。

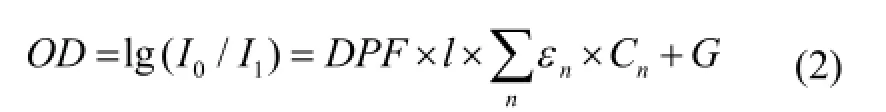
式(2)中使用DPF因子修正光子传播的路径。

因为常数项G在较小的距离内差异较小，可以通过使用双色光进行入射和检测对常数G进行消除，达到对血氧进行测量的目的[2-6]。

在利用式(2)进行血氧浓度计算时通常使用的是最小二乘拟合的方法，通过建立血氧饱和度的线性模型，完成对血氧含量的估计。因此，修正的朗伯—比尔定律可以简写成式(3)。

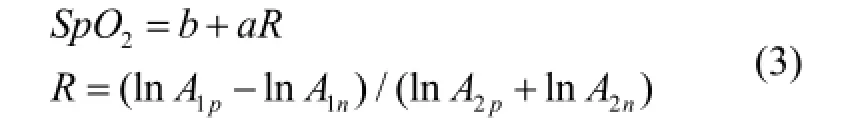
其中R项为测量双波长下的血氧峰谷对数差值的比。Aip为第i种波长下测量得到的电压峰值，Ain为第i种波长下测量得到的电压谷值。

然而使用最小二乘的方法建立起来的血氧估计式，忽略了光在组织内的散射作用，同时这种方法忽略了测量时血氧的交直流变化，因此在精度方面会有一定的损失[8-10]。本文通过使用建立双波长下血氧各状态下的多参数回归方程，对血氧饱和度进行估计，如式(4)所示：

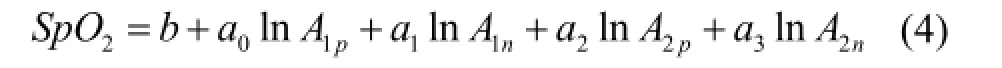
为验证方法的可行性，设计了血氧检测的硬件装置，对相关数据进行测量，然后与朗博—比尔定律所得的结果进行比较并分析。

2 装置设计

因本文所检测的对象主要为氧合血红蛋白和还原血红蛋白，因此需要对两者关于光谱的作用进行明确，根据不同波长下氧合血红蛋白和还原血红蛋白吸收系数可以发现：对于氧合血红蛋白来讲，随着近红外光光谱波长的逐渐增加，氧合血红蛋白的吸收系数也在逐渐提高，因此所使用的近红外波长不能太大，以利于输出光强的检测。与氧合血红蛋白相反，还原血红蛋白的吸收系数会随着近红外光谱的波长的增加而成负相关的特性。这两种截然相反的特点使双波长无创血氧检测的波长选择被确定在一个小区间内。本文的双波长选择为两者光谱交叉点的两端吸收系数较为接近的两个波长，分别为760 nm和850 nm。

本文通过使用MSP430单片机对波长为760 nm和 850 nm的二极对管进行驱动并检测，获得所需数据，其系统框图如图1所示。

图1 无创血氧检测系统框图Fig.1 Noninvasive detection of blood oxygen system diagram

系统通过控制电路对二极管进行时序控制，通过使用桥式电路对近红外二极管进行功率驱动，达到近红外光线的控制及发射。采集电路采用日本滨松公司生产的光电倍增管对由皮下出射信号进行检测，完成原理中要求的血液中各状态值的测量。最后采集数据在MCU中采用16进制的方式发送到上位机，上位机通过Matlab进行数据分析并计算得到血氧数据。

3 实验数据及分析

为检测方法的正确性及测量装置的精确性，使用北京超思电子技术有限公司出品的血氧检测仪作为参考仪器，其具有1%的测量精度。通过将同一时刻的参考仪器与自制仪器测量结果同时输入，并分别使用不同方法进行计算对比，可以得到两种方法之间的差别和特性，达到对方法验证的目的。

因血氧数据会随着人体运动和人体状态不同而波动，因此数据需要同步采集，同时血氧参数会因被测对象的不同而有较为明显的差别。系统对20个被测对象进行血氧测量，其测量过程首先要求被测对象静坐于桌前，同时进行深呼吸随后进行憋气以保证血氧可以充分变化。当被测对象保持静止时，使用两种仪器同时对被测血氧数据进行采集。其中某一被测对象的自制系统采样结果与参考仪器的检测结果如图2和图3所示。

图2 自制系统采样预处理数据结果Fig.2 Results of pretreated sample data

由图2可见，自制系统采样的2种波长光下血氧出射值具有缓慢的增加和降低的变化趋势，这符合前述血氧在对应近红外光波长下的透射规律。而且使用参考仪器对血氧饱和度进行测量的结果（图3）可见，随着被测对象的憋气时间增长，血氧饱和度呈下降趋势。这和自制仪器的预处理结果的趋势相吻合，证明了采样数据的可靠性。为测试两种算法的精度，分别带入自制系统的采样结果进行计算。

图3 参考仪器输出结果图Fig.3 Results of reference measurement

首先利用常用的修正朗伯—比尔定律对相关参数进行计算，利用前述公式可以计算相关R值与血氧饱和度的散点图，同时还可以获得每一个血氧饱和值对应的R值的均值，其散点图和均值如图4所示。

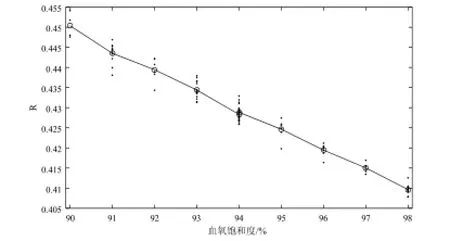
图4 自制系统采集并计算R值结果图Fig.4 Scatter of R value and oxygen percentage

如图4可见，R值随着血氧饱和度的升高而降低，这符合修正的朗伯—比尔定律中关于R值与血氧饱和度值呈反比的结论，也证明了自制系统的采集结果的可靠性和有效性。因散点分布存在交叠情况，采用Matlab对数据进行处理。首先对采样数据进行均值处理，随后将均值带入式(3)中进行计算，可以获得其对应的系数。每段血氧饱和度不变的时间段设为一个采样点，计算结果及与参考值的残差如图5所示。

根据本文所述方法，使用多元回归线性回归的方式对数据进行处理，其计算式如式4所示。同样使用均值后将计算值和参考值进行比较，其结果如图6所示：

由图6可知，利用多元回归分析，因为使用了更多维度的血氧相关量，所以可以获得更为精确的结果。图6相比图5，残差分布得更为均匀，而且总残差要小于前者。因此可以证明，利用多元回归分析建立的模型相比修正的朗伯—比尔定律更容易获得精确的结果，效果更好，可以在一定程度上降低仪器噪声所带来的误差等因素。

图5 利用修正的朗伯-比尔定律获得的血氧饱和值与参考值对比图Fig.5 Compared with the reference value of blood oxygen percentage with amended Lambert-Beer Law

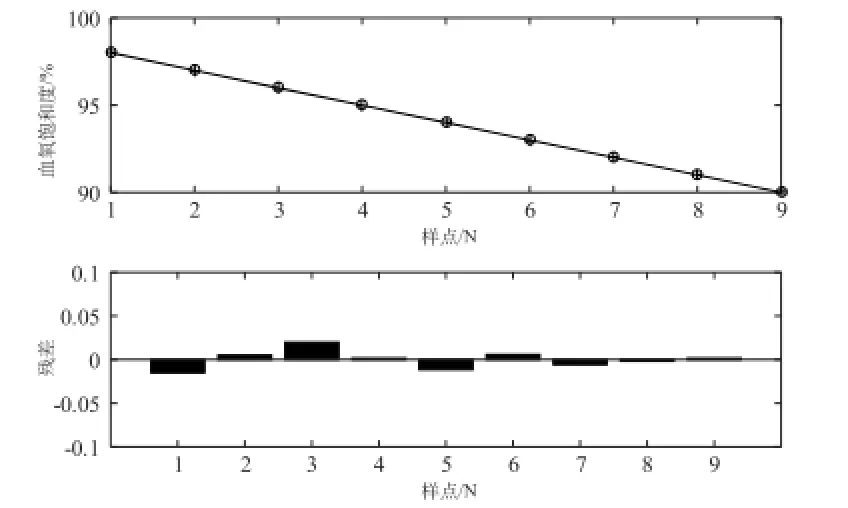
图6 使用多元回归方法获得的血氧饱和值和参考值的对比图Fig.6 Compared with the reference value of oxygen percentage with multiple regression analysis

4 结论

通过对比的方法，本文设计了血氧饱和度检测的内部算法及预测模型，同时设计了相关的硬件实验系统，证明了利用多元回归算法的血氧饱和预测值可以获得更好的精度。算法使用多元线性构建，利于硬件编写函数进行实现，相比原有的修正的朗伯—比尔定律，更利于硬件实现快速的检测，为建模分析血氧饱和度和硬件实现提供了新的研究思路和解决方案。

[1] 高遵伯. 基于DSP的脉搏血氧饱和度测量仪的研制[D]. 长沙: 国防科学技术大学, 2002.

[2] 谢正洋. 无创血氧饱和度的测量及无线监测系统的研制[D]. 苏州: 苏州大学, 2009.

[3] 刘光达, 郭维, 朱平, 白明明. 基于容积波分析的血氧饱和度测量系统[J]. 激光与红外, 2009, (2): 169-172.

[4] 张晓军. 基于ARM的血氧饱和度测量仪研制[D]. 厦门: 厦门大学, 2007.

[5] 张根选, 石波, 刘胜洋, 陈建方, TSAUYoung. 一种高效实时脉搏血氧监测系统的研究[J]. 激光与红外, 2014, (2): 187-191.

[6] 王晓飞, 赵文俊. 基于动态光谱法的多波长脉搏血氧饱和度测量[J]. 光谱学与光谱分析, 2014, (5): 1323-1326.

[7] 房磊. 无创血氧饱和度测量系统的设计与实现[D]. 武汉: 华中科技大学, 2012.

[8] 李金海. 多元回归分析在预测中的应用[J]. 河北工业大学学报, 1996, (3): 57-61.

[9] 傅惠民, 岳晓蕊. 多元混合数据回归分析方法[J]. 航空动力学报, 2011, (1): 173-177.

[10] 石波, 刘胜洋, 陈建方, 等. 线性回归算法提取脉搏血氧特征值初步验证[J]. 中国医学物理学杂志, 2013, (1): 3913-3916.

Study of Blood Oxygen Measuring Method Based on Multiple Regression Analysis

【Writers】JIN Yibo, WANG Qinmei

In the traditional measurement of blood oxygen , amended Lambert-Beer Law is used to calculate the oxygen percentage in the blood. On the one hand, results will be acquired slowly because of the divide operation. On the other hand, amount of precision will be lost because of the errors by using ratio, which leads to the low accuracy results. In order to solve this problem, multiple regression analysis is used in this paper to measure and evaluate the oxygen percentage in the blood. Results show that, compared to the ratio, the new method has an obvious advantage and can be realized by hardware more easily.

blood oxygen detection, multiple regression analysis

Wenzhou Medical University, Wenzhou, 325027

TH772

A

10.3969/j.issn.1671-7104.2016.04.007

1671-7104(2016)04-0260-03

2016-02-23

王勤美，E-mail: wqm55@hotmail.com