高频曲柄滑块机构的动力学分析与轴承温度场分析

徐一珣

(上海交通大学机械与动力工程学院，上海 200030)

高频曲柄滑块机构的动力学分析与轴承温度场分析

徐一珣

(上海交通大学机械与动力工程学院，上海 200030)

曲柄滑块机构是常见的通用机构，高频工况下的曲柄滑块机构，若不考虑质量与摩擦，其计算结果和实际结果的相差较大，不能很好的指导实际的设计。本文通过对“发动机链条高频耐久测试台架”中的曲柄滑块机构进行研究，在考虑构建质量和轴承部位摩擦的基础上，分析各个运动部件的运动规律、受力情况，建立模型动力学模型和热力学模型，估算惯性载荷和摩擦带来的影响，并由动力学分析得到的关节轴承处摩擦功率的估算，计算轴承在高频运动过程中的发热和温度场分布。并将计算结果和试验结果做比对，对模型中的参数选择进行修正，以得到更为精确的计算模型，为该测试台架曲柄滑块机构的开发设计，提供参考依据。

曲柄滑块机构 动力学分析 轴承温度场分析

0 引言

曲柄滑块机构是机械设计中常见的通用机构，低频工况下，在计算曲柄滑块机构的时候，考虑或者不考虑质量和摩擦对结果影响不大。而在高频工况下的曲柄滑块机构，若不考虑质量与摩擦，其计算结果和实际结果的相差较大，不能很好的指导实际的设计。

本人在开发“发动机链条高频耐久测试台架”的过程中遇到的主要问题是，在高频工况下，关节轴承部位的发热和温度分布，并无有效的工具可以进行提前计算和分析。因此，如何设计出合适的计算方法，有效仿真机构的动力学特性和关节轴承处的温度分布，预测轴承的最高温度，以获得对机构设计有效的支持，对于高频曲柄滑块机构的设计有重要的意义。

1 测试台主要结构与工作原理

根据以上的测试台架设计要求，为了兼顾摆动角度+/-10°与变化的力加载50-300 N，故选取曲柄连杆滑块机构作为该链条测试台的主要执行机构，并且使用弹簧实现变化的加载。

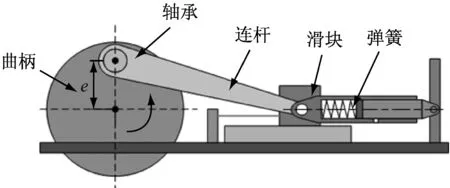
图1 测试台主要机构Fig.1

被测件之一的链板和弹簧机构相对固定，被测件之二链条销和连杆相对固定，利用曲柄连杆滑块机构中连杆的摆动形成+/-10°的摆动角度，以此来模拟实际发动机工作是链板和链条销之间的相对运动和交变载荷。

2 考虑质量和关节轴承摩擦的动力学建模

使用动态静力分析的解析方法，首先对曲柄滑块机构进行运动分析，得到机构的位置参数，继而在考虑构件质量和轴承摩擦的条件下，对曲柄滑块机构进行动力学分析。继而进行计算模型的矩阵化，使用MathCAD软件完成计算模型的建立。

使用机构动态静力分析的解析方法，此处考虑构件的自身重力及运动副之间的摩擦力，并且考虑构件本身的惯性力。

经过对于每一个杆件的受力分析，可得如下矩阵：AR=B1-B

(1) 式中：

矩阵A为一个8×8的已知方阵，此矩阵仅仅与杆件的质心位置有关：

(2)

矩阵B为一个8维的已知列阵，其中包含该机构所受的外力、外力矩：

(3)

矩阵B1为一个8维的已知列阵，其中包括该机构所受的惯性力和惯性力矩：

(4)

矩阵R为一个8维的未知矩阵，R中包含了曲柄滑块机构各个运动副中的反力在x、y两个坐标轴方向的分量、对于滑块的支反力N和作用于原动构件上的平衡力矩MA：

(5)

按照实际测试设备的边界条件，使用软件MathCAD为矩阵求解建立模型并计算B处轴承的摩擦功率。

Max=126.224WMin=24.761W

图3 WB计算结果Fig.3

B处轴承的摩擦功率WB在同时考虑构件质量和轴承摩擦的情况下的计算结果的幅值变化，比仅仅考虑轴承摩擦大，质量和摩擦都是影响WB的重要因素，特别在高频的工况下，都不可忽略。

3 关节轴承温度场计算

RC热电模拟法，是用来计算分析物体内部温度场的一种算法。其理论依据是根据热、电在其传递规律上的相似性，即导热过程和导电过程都可以用一个可以类比的微分方程来表示，因此可以使用热电模拟的方法来进行温度场计算。

将以上动力学计算得到的B处关节轴承的摩擦扭矩和功率作为输入，使用RC热电模拟法，首先在关节轴承内圈、外圈、滚道、端面、轴承座和驱动轴上设置了一定数量的温度计算节点。继而使用RC热电模拟法和MathCAD软件进行计算，得到轴承各个关键部位的温度分布。在后续的试验过程中，将进一步对热分析模型进行参数修正，使之成为更符合实际的计算模型。

(1) 温度节点系统设置：

根据RC热电模拟法的计算方式，首先在轴承和轴承座构成的系统当中，假设若干代表物体各个位置的温度节点。以此来建立热传递的网络，并且作为之后转化为电路的输入。

图4 温度节点系统设置

(2) RC热电模拟法计算本轴承温度的假设条件：

该轴承的温度场计算，是将实际情况抽象为11组节点定义的热传递网络的理想概括。各类边界条件的设置也不完全和实际情况一致，计算模型是理想情况的抽象。如下是本次计算的假设条件：

假设用11个温度节点，可以来模拟该系统各个位置，包括轴承座左右端面，外圈，轴承内圈、轴承外圈、轴承的球体和轴的温度分布情况。即假设11个温度节点以外的点都可以被该11个典型点所代表。

假设环境温度始终为20 ℃，且保持温度均匀和恒定，不会随着机构运行的发热而改变。

假设润滑油的温度为20 ℃，且保持温度均匀和恒定，不会随着机构运行的发热而改变。

假设空气环境为自然对流状态。与空气对流的热传递系数初始假设为50 W/m2*K。其后将根据特殊点的实测温度，来修正对于热传递系数的定义，以得到一个更接近实际工况的计算模型。

假设材料的热属性为常数，在实验的过程中，导热系数不会发生改变。如：空气的表面对流换热系数的数值，与换热过程中空气的物理性质、换热表面的形状尺寸和相对位置、表面与流体之间的温差、流体的流速及流体有无相变等都有密切关系。然而为了计算的简化，将空气的表面对流换热系数看做是常数，在计算的模型和试验的过程中不会发生改变。

(3) 根据RC热电模拟法的计算思路，利用热、电在其传递规律上的相似性，将以上热传导网络模型和电阻电路模型进行类比和转换。以此来研究和计算热传递的方式和温度场分布的情况。

在导热计算的过程中：导热量Φ或热流密度q可以对应电流强度I。传热温差Δt对应于电压U。导热热阻对应电阻R。

根据以上的计算思路，热量传递的方式分析如下：

节点1、3、4、5、7、8、10、11所代表的轴承座端面及外圆的各个节点与空气之间的热传递是以对流的形式出现的。

节点2、6、7所代表的深沟球轴承DGBB6304的外圈、球体与内圈与润滑油之间的热传递是是以对流的形式出现的。

其余相邻节点之间的热传递是金属与金属之间的传递，方式为热传导，主要包括轴承和轴承座之间的热传导、轴承和轴之间的热传导、轴承座和轴之间的热传导，以及轴承座的内部、轴承的内部、轴的内部不同温度区域之间的热传导。

此外，在节点2、6、7所代表的深沟球轴承DGBB6304的外圈、球体与内圈之间，外圈和球体，内圈和球体之间，由于轴承实际运转中的摩擦而造成的发热，是该热传递网络之中的热量来源。其后的模型计算当中，将选用第二章中计算所得的关节轴承摩擦功率作为发热功率的输入。

综上，可将温度节点图中的模型转换为下图中的电阻电压电流网络模型。

图5 温度节点转换为RC热电模拟法Fig.5

如电流流经每个节点的平衡方程一样，输入每一个温度节点的热量和输出该节点的热量持平。故能根据11个节点的热量输入输出，可得到11个平衡方程。

使用MathCAD建模，计算可得：

4 计算系数修正试验

系数修正试验，其目的为得到与实际工况更接近的空气的表面对流换热系数。故使用关节轴承上有代表性的特定点在特定工况下的试验结果，聚焦于便于测量且计算下温度较高的节点11，在20 Hz的工况下，测试该节点的温度。继而使用该点的试验测量结果对热力学模型中的空气的表面对流换热系数的设置进行修正，以得到与实际工况更为符合的计算模型。

试验设备的设计为简化后的台架核心机构。主体部分为电机转作皮带传动，分为左右两支曲柄连杆滑块机构，以平衡部分惯性力。

表1 自然对流下轴承各个节点的温度分布

试验的采集设备如下图，组成部分包括：

(1) 测量弹簧力:力传感器U2B 1KN

(2) 测量曲柄连杆轴承处温度：温度传感器PT100，并且采用贴片测温的方式测量

(3) 数据采集和处理器：MGC及MX840A

按照测温点T11在连续运行60分钟之后，达到的温度稳态时的温度62.2 ℃，对模型中的与空气对流的热交换系数进行修正。

修正计算如下表，修正前取用的热交换系数为50 W/m2*K，温度计算结果和该点实际测量的差异为17.67%。修正后取用热交换系数为75 W/m2*K，使用修正后的系数进行计算，可得与测量结果的差异为0.07%。

图6 测量系统布置Fig.6

实际测量结果原始计算结果修正后计算结果与空气对流的热交换系数(W/m2∗K)5075温度(℃)62．275．55262．241与测量结果的差异17．67%0．07%

5 试验验证模型结果

该实验使得曲柄连杆滑块机分别在3 Hz，10 Hz，20 Hz，30 Hz的工况中运行，并在60分钟之内

持续监控T1，T3，T5，T11四个测点的温度变化，以最终达到热平衡的温度温度，作为验计算结果的输入条件。

四个温度测点的试验结果、计算结果以及偏差分析列举如下表：

表3 温度测点T1的偏差

表4 温度测点T3的偏差

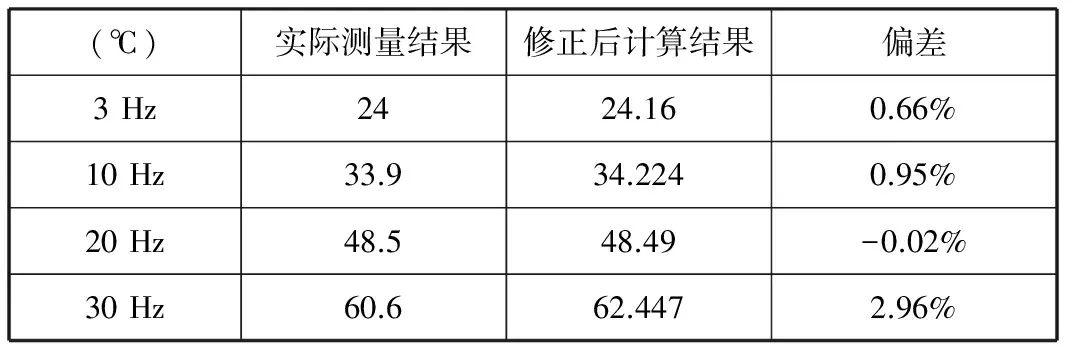
表5 温度测点T5的偏差

表6 温度测点T11的偏差

对上述结果中的偏差值进行分析：

(1) 在以运动频率3 Hz为代表的低频的工况下，试验结果和计算结果，于四个测温点，偏差最大仅为1.11%。

(2) 在以运动频率10 Hz为代表的中频工况下，试验结果和计算结果，于四个测温点，偏差最大为2.49%。

(3) 在以运动频率20 Hz与30 Hz为代表的高频工况下，试验结果和计算结果，于四个测温点，偏差最大分别为2.97%与3.71%。

由此可见，从相对的角度来说，运动频率越高，模型计算的误差会逐步放大。从实际运用的角度来说，这样的精度是可以接受的。

6 总结

曲柄连杆滑块在高频工况下的关节轴承处的轴承发热，是一个常见的问题，过大的摩擦造成的高温将破坏轴承的稳定性能和寿命，将严重影响测试台架设备的性能实现和工作寿命。

本文使用在20 Hz的运动工况下，动力学计算得到的关节轴承处的摩擦功率作为输入，在关节轴承内圈、外圈、滚道、端面、轴承座和驱动轴上设置了一定数量的温度计算节点。使用RC热电模拟法将热传递的网络转化为电路，和MathCAD软件结合使用进行计算，在计算得到物体内部各个点的导热量和热阻之后，计算得到对应的温度差，并由此可以推得各个点的温度分布。

继而设计系数修正试验，使用关节轴承上有代表性的特定点，在特定工况20 Hz的运行速度下，测试该节点在达到热平衡时的温度。并使用该点的试验测量结果对热力学模型中的空气的表面对流换热系数的设置进行修正，以得到与实际工况更为符合的计算模型。

[1] 张 策，机械动力学(第二版)，北京，高等教育出版社，2008.1，1-37页

[2] 张天孙，传热学(第二版)，北京，中国电力出版社，2006.2，22-32页

[3] T.A.Harris, M.N.Kotzalas，滚动轴承分析，第一卷，轴承技术的基本概念，北京，机械工业出版社，2011.1，181-197页

High frequency slider-crank mechanism dynamic analysis and bearing temperature analysis

XuYixun

(SchoolofMechanicalEngineering,ShanghaiJiaoTongUniversity,Shanghai200030)

Slider-crank mechanism is a common mechanism. The big difference between calculation results and actual results will be showed under high frequency condition without considering the mass and friction which cannot guide design with high accuracy. Based on the research of slider-crank mechanism from ‘High frequency single link chain wear test rig’ project, the author try to build the dynamic model and thermodynamic model with considering the mass of components and friction from bearing. After the compare with the results from calculation and experiment, calculation parameters in model be adjusted to increase the accurate of calculation. The calculation model can provide the method to guide the development and design of the slider-crank mechanism in the test rig.

Slider-crank mechanism Dynamic analysis Thermodynamic analysis of bearing

1006-8244(2016)04-038-06

TH132

B