时变有界变采样网络控制系统的保性能控制

李 媛， 张国山， 孙琨秋

(1.天津大学 电气与自动化工程学院， 天津 300072； 2.沈阳工业大学 理学院， 辽宁 沈阳 110870)



时变有界变采样网络控制系统的保性能控制

李 媛1，2， 张国山1， 孙琨秋2

(1.天津大学 电气与自动化工程学院， 天津 300072； 2.沈阳工业大学 理学院， 辽宁 沈阳 110870)

考虑采样周期和时延是时变不确定的，研究网络控制系统的保性能控制问题.首先将其建模成离散系统，将周期和时延的不确定性利用泰勒公式转化成系统矩阵的不确定性，并将系统转化为动态区间系统，通过求解线性矩阵不等式的最优解设计最优保性能控制器.由于该方法同时考虑了周期和时延的变化，因此设计的控制器更符合实际，仿真结果表明该方法简单有效.

网络控制系统(NCSs)； 变采样周期； 区间系统； 保性能控制

网络控制系统(networked control system，NCSs)是一种网络化、分布式的控制系统，是通过网络构成闭环的反馈控制系统，又称为基于网络的控制系统、网络化控制系统[1-3].与传统的点对点控制系统相比，NCSs具有很多优点，被广泛用于设备制造、生产过程、交通通讯、航空航天等控制领域.但是NCSs利用网络给控制系统带来各种优点的同时，它本身也存在一些问题，比如数据传输时延、数据包的丢失、采样周期的变化、单包传输、多包传输、噪声污染等，这些问题使控制系统的稳定性降低，因此需要对NCSs进行深入研究.近年来，关于NCSs得到许多研究成果，例如系统的模型建立与稳定性分析[4-6]、鲁棒与H∞控制分析[7-9]、最优保性能控制[10-12]，以及相关系统的控制器设计问题[13-15]等.

在NCSs的研究过程中，通常假设传感器是定长采样周期，然而在实际的NCSs中，由于负载变化、网络影响、器件故障及外部干扰等因素，往往会导致采样周期发生抖动，在某个标称值上下波动，从而产生采样周期的不确定，因此系统可以描述为区间控制系统[16].文献[4]是将时变采样周期NCSs的闭环反馈系统转化为动态区间系统，并对其进行了稳定性研究.文献[16]研究了连续区间系统的鲁棒H∞控制，利用Riccati方程获得状态反馈控制器.文献[17]分别就离散型和连续型两类区间系统的鲁棒控制问题做出了详尽的研究.文献[18]讨论了区间系统的鲁棒H∞稳定性.文献[19]研究了一类不确定系统的鲁棒稳定性问题，并将其结果推广到区间系统的鲁棒稳定性分析中，得到了区间系统鲁棒稳定的新判据.文献[20]研究了一类不确定时延NCSs，将系统化为变采样NCSs，通过动态输出反馈研究系统的建模和保性能控制.文献[10]虽然研究了NCSs的鲁棒保性能控制，但是采样周期是定长.文献[21]研究了一类具有采样抖动和数据包丢失NCSs的鲁棒H∞控制方法，将闭环系统转化为具有不确定性的离散线性切换系统，但并没有对NCSs的保性能控制进行研究.在信道带宽有限和共享CPU资源的情况下，为了充分利用资源，当采样周期在某一有界范围内发生变化时，研究NCSs的建模和控制器设计等问题，具有一定的理论和现实意义.

本文研究NCSs的最优保性能控制器的设计问题，其中采样周期和时延都是时变有界的.首先利用泰勒公式，将采样周期的波动和时延的不确定性转化为系统的不确定性，根据其不确定范围将其建立成动态区间系统.在此基础上，结合线性矩阵不等式方法，设计了系统的最优保性能控制器，并给出最优保性能指标上界.最后通过实例仿真验证了该方法的有效性.

1 系统模型的建立与分析

1.1 系统分析

考虑如图1所示的网络控制系统，线性时不变被控对象为：

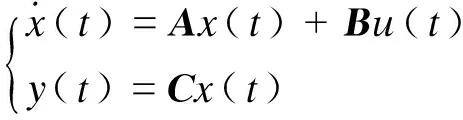
(1)

其中x(t)∈Rn，u(t)∈Rr,y(t)∈Rm,x(t)为被控对象的状态，u(t)为被控对象的控制输入，y(t)为被控对象的测量输出，A、B、C为相应的适当维数的常矩阵.

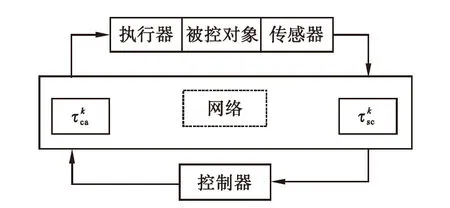
图1 网络控制系统模型

Fig.1 The structure of networked control systems

为了便于分析，对系统做出如下假设：

(1) 假设传感器采用时钟驱动，控制器和执行器采用事件驱动，采样时刻为tk,k∈N.设hk为连续两次采样时间的间隔，hk=tk+1-tk；

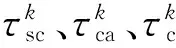
(3) 采样周期hk和τk是时变不确定的，但是都有界，hk=h0+Δh，τk≤hk，其中h0为系统的定采样周期，因此Δh也有界，而且|Δh|足够小，使得传感器能够正常运行.

由于执行器端有零阶保持器，系统的被控对象的输入即控制器输出的控制值是分段的，即

考虑时延的影响，按照采样周期hk对被控对象进行离散化，得到离散化模型为

(2)

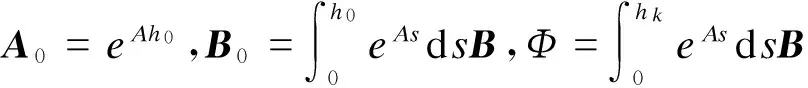
Ad=eAhk=eAh0+(eAhk-eAh0)=

eAh0+(eA(h0+Δh)-eAh0)=

eAh0+eAh0(eAΔh-I)

因为|Δh|足够小，由泰勒公式得eAΔh=AΔh+I，进而得到

Ad=eAh0+eAh0(AΔh+I-I)=

eAh0+eAh0AΔh=A0+A0ΔhA=

A0+ΔA

其中ΔA=A0ΔhA.

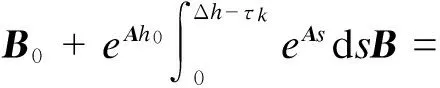
B0+ΔB

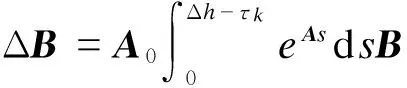
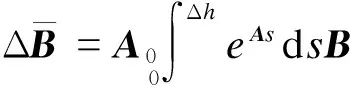
最终整理得到

ΔB)u(k-1)+(B0+ΔB)u(k)

(3)

为便于研究，设z(k)=[x(k) u(k-1)]T，式(3)可改写为

进一步离散化模型可简化为

z(k+1)=Hz(k)+Γu(k)

(4)

其中

1.2 区间系统建模

假设矩阵

[hij](n+r)×(n+r)

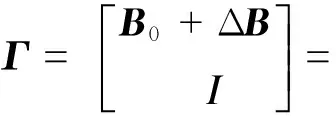
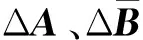
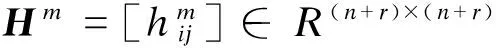
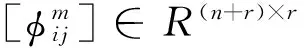
其中

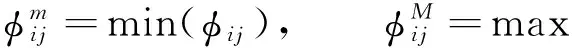
则Hm≤H≤HM,Γm≤Γ≤ΓM.

定义

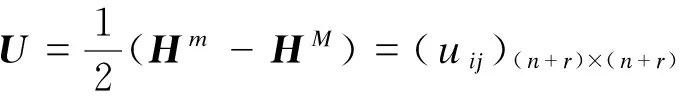
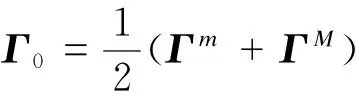
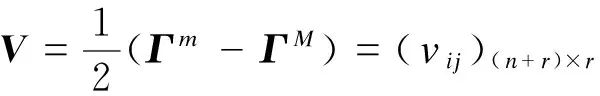
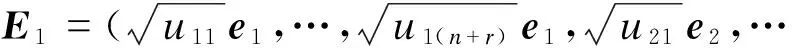
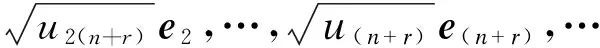
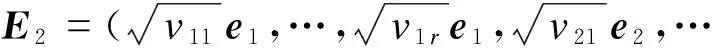
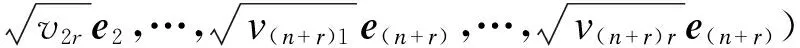
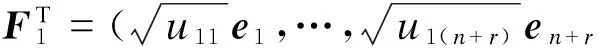
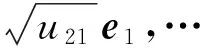
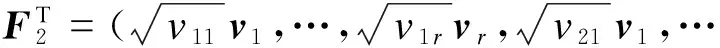
其中ei为(n+r)维单位矩阵的第i个列向量，vi为r维单位矩阵的第i个列向量，并且设

Σ1=diag(ε11,…ε1(n+r),ε21,…ε2(n+r),

…ε(n+r)1,…ε(n+r)(n+r)),

|εij|≤1, 1≤i,j≤n+r

Σ2=diag(ε11,…ε1r,ε21,…ε2r,…ε(n+r)1,

…,ε(n+r)r),

|εij|≤1,1≤i≤n+r, 1≤j≤r

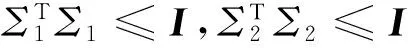
因此区间矩阵可改述为

H=H0+E1Σ1F1,

Γ=Γ0+E2Σ2F2

最终系统模型可化为

z(k+1)=(H0+E1Σ1F1)z(k)+

(Γ0+E2Σ2F2)u(k)

(5)

2 最优保性能控制器设计

2.1 相关知识介绍

对于系统(4)(公式(4)，以下同)，定义一个性能指标

(6)

其中Q、R为已知的对称正定加权矩阵.

定义1[22]对系统(4)和性能指标(6)，若存在一个矩阵K和一个正定对称矩阵P，使得对区间矩阵H、Γ满足

zT(k)[(H-ΓK)TP(H-ΓK)]z(k)-

zT(k)Pz(k)+zT(k)(Q+

KTRK)z(k)<0

(7)

则控制器u(k)=-Kz(k)称为系统的一个具有性能矩阵P的二次保性能控制器.

引理1[22]设A是任一方阵，则存在矩阵P>0，使得ATPA-P+T<0，当且仅当存在对称矩阵X>0，使得

引理2[22]给定适当维数的矩阵Y、D、E，其中Y是对称的，则

Y+DFE+ETFTDT<0

对所有满足FTF≤I的F成立，当且仅当存在一个常数ε>0，使得

Y+εDDT+ε-1ETE<0

2.2 保性能控制器设计

定理1 对于系统(4)，若存在二次保性能控制器u(k)=-Kz(k)，则对所有的不确定性，闭环系统

z(k+1)=(H-ΓK)z(k)

(8)

证明： 如果u(k)=-Kz(k)是系统(4)的一个具有性能矩阵P的二次保性能控制器，定义Lyapunov函数V(k)=zT(k)Pz(k)，则根据定义1知，沿闭环系统(8)的任意轨线，对区间矩阵H、Γ，可以得到

ΔV(k)=V(k+1)-V(k)=

[(H-ΓK)z(k)]TP[(H-ΓK)z(k)]-

z(k)TPz(k)<-zT(k)(Q+KTPK)z(k)<0

因此闭环系统是二次稳定的.

再者，从上式可以得到

zT(k)(Q+KTRK)z(k)=zT(k)Qz(k)+

u(k)TRu(k)<-ΔV(k)

在上式的两边从k=0到k=∞求和，利用闭环系统的二次稳定性，可以得到

接下来将给出系统(4)的保性能控制器设计方法.

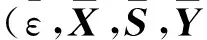
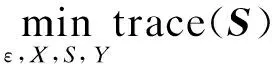
(9)

s.t

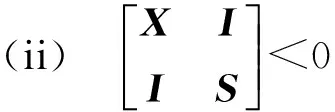
证明：由定义1知，若系统存在一个保性能控制器u(k)=-Kz(k)，式(7)就成立，则对于所有非零z(k)和所有的不确定性，下式成立

[(H-ΓK)TP(H-ΓK)]-

P+(Q+KTRK)<0

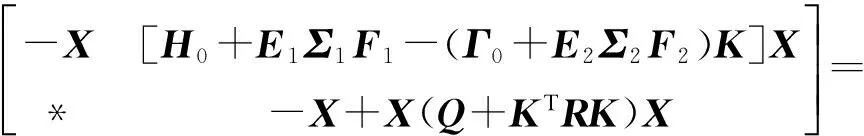
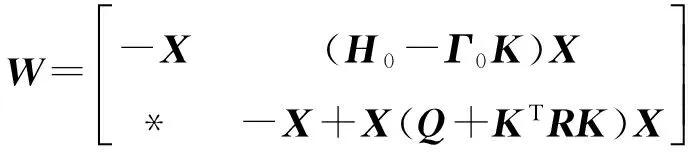
进而可以改写为

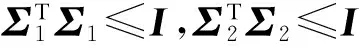
成立.由引理2可得，上述不等式成立当且仅当存在一个常数ε>0，使得

把对称矩阵W代入，可得

应用Schur补性质，上式可以写成

在上式中如果取Y=KX，则得到优化问题(9)中的约束条件(i).再应用Schur补性质，优化问题(9)中的约束条件(ii)等价于S-X-1>0，即S>X-1>0.Trace(S)能够保证Trace(X)的最小化，而且优化问题(9)是一个凸优化的问题，能够达到全局的最小值.

优化问题(9)以及相应的约束条件所涉及的线性矩阵不等式都可以通过Matlab软件中LMI工具箱中的求解器进行求解，计算起来方便快捷.

3 数值仿真

被控对象的模型如下：

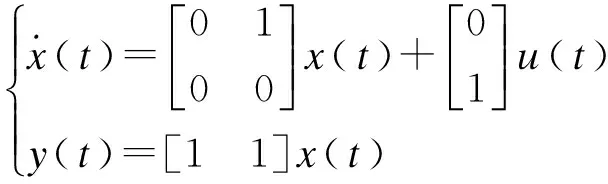
利用文中给出的控制器的设计方法进行求解.hk和τk的有界区间为：

hk∈[0.45,0.55],τk∈[0,0.05],

Δh∈[-0.05,0.05]

通过求解可以得到区间矩阵如下：

性能指标加权矩阵取为Q=I,R=1.利用Matlab的LMI工具箱中的目标函数最小化工具mincx，得到最优解分别为：

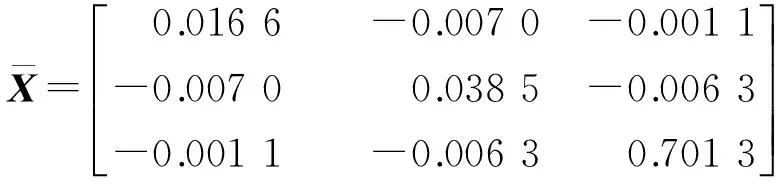
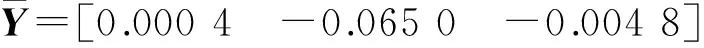
ε=0.437 4

进而得到最优保性能控制器为：

-[0.749 8 1.831 5 0.024 5]z(k)

图2 有界采样周期序列

Fig.2 Bounded sampling period sequence

图3 有界时延序列

Fig.3 Bounded time delay sequence

在上述所得控制器的作用下，当被控对象的初始状态为x(0)=[2;1]，能够得到闭环系统的状态响应曲线,如图4所示，显然闭环系统是渐近稳定的.

图4 状态响应和输出曲线

Fig.4 State response and output curves of the closed-loop systems

4 结 论

针对变采样周期和时延时变有界的网络控制系统，利用泰勒公式和区间系统理论，将其建立成动态区间系统，利用线性矩阵不等式的方法设计保性能控制器.在设计过程中，利用Matlab软件中LMI工具箱对线性矩阵不等式求解，方法简便.最后通过实例仿真表明该方法的有效性.为寻求控制系统能够更加稳定，系统中存在的数据丢包和外部扰动等现象，应得到更多的密切关注.

[1] 孙阳.网络控制系统的稳定性分析及其保性能控制[D].沈阳：东北大学，2013:1-3.

[2] 陈惠英.资源受限网络控制系统控制与调度方法研究[D].杭州：浙江工业大学，2008:1-5.

[3] 陈惠英，李祖欣，王培良.具有时变采样周期和时延的NCS的H∞控制[C]//中国自动化学会控制理论专业委员会B卷，烟台：中国自动化学会控制理论专业委员会，2011:4521-4526.

[4] LIU F C，YAO Y，HE F H，et al.Stability Analysis of Networked Control Systems with Time-varying Sampling Periods[J].Journal Control Theory Application，2008，6(1):22-25.

[5] XIE G M，WANG L.Stabilization of Networked Control Systems with Time-varying Network-induced Delay[J].IEEE Conference on Decision and Control，2004，4(43):3551-3557.

[6] 徐君群，张建雄，庞明宝.2 个时滞复杂动态网络的广义同步[J].天津大学学报，2014，47(1)：81-85.

[7] 王玉龙，杨光红.具有时变采样周期的网络控制系统的H∞控制[J].信息与控制，2007，36(3)：278-284.

[8] 李艳辉，张莹.变采样周期和数据包随机丢失的NCS鲁棒H∞控制[J].计算机技术与自动化，2013，32(3)：1-5.

[9] QIAN P，WANG W H，LI X Q，et al.H∞Robust Control for Networked Control System with Short Time-delay[J].Applied Mechanics and Materials，2014，556/562:5501-5505.

[10]张喜民，李建东，张建国.网络控制系统的鲁棒保性能控制[J].西安电子科技大学学报(自然科学版)，2008，35(1)：96-100.

[11]陈惠英，李祖欣，王培良.变采样网络控制系统的最优保性能控制[J].信息与控制，2011，40(5)：646-651，657.

[12]樊金荣.变采样周期网络控制系统的最优保性能控制[J].武汉大学学报(工学版)，2011，44(6)：806-811.

[13]江兵，张崇巍.一类不确定时延的NCS的保性能控制律设计[J].系统工程与电子技术，2010，32(3)：645-649.

[14]樊金荣.时变采样网络控制系统的容错控制器设计[J].中南民族大学学报(自然科学版)，2011，30(3)：80-84.

[15]DENG J Q，CUI H.Research on State Feedback Controller of the Networked Control System with Long Delay[J].Applied Mechanics and Materials，2014，536/537：1183-1186.

[16]吴方向，史忠科，戴冠中.区间系统的鲁棒H∞控制[J].自动化学报，1999，25(5)：703-708.

[17]申涛，诸静.区间系统的鲁棒稳定性分析[J].电路与系统学报，2005，10(2)：79-82.

[18]SEZER M E，SILJAK D D.On Stability of Interval Matrices[J].IEEE Trans on Automatic Control，1994，39(2):368-371.

[19]申涛，王孝红，袁铸钢.一类不确定系统的鲁棒稳定性分析[J].自动化学报，2007，33(4)：426-427.

[20]薛燕，刘克.变采样网络控制系统的最优保性能控制[J].计算机工程与设计，2009，30(2)：294-297.

[21]HUA C C，YU S C，GUAN X P.A RobustH∞Control Approach for a Class of Networked Control Systems with Sampling Jitter and Packet-dropout[J].International Journal of Control，Automation and Systems，2014，12(4):759-768.

[22]俞立.鲁棒控制：线性矩阵不等式处理方法[M].北京：清华大学出版社，2002:214-267.

Guaranteed Cost Control for NCSs with Time-varying Bounded Sampling

LI Yuan1，2， ZHANG Guo-shan1， SUN Kun-qiu2

(1.Tianjin University， Tianjin 300072， China；2.Shenyang University of Technology， Shenyang 110870， China)

Considered sampling period and time delay was time-varying and bounded，networked control systems with the guaranteed cost control problem was studied.Firstly，it was modeled as a class of discrete systems.Next，the system was transformed into a time-varying dynamic interval system with Taylor formula，where the uncertainties of time-varying sampling period and time delay were treated as the uncertainties of the system matrices.Then，the design of the optimal guaranteed cost controller was proposed in terms of linear matrix inequalities.Both the change of period and time delay are considered in this method，so the proposed controller is more in line with the reality，and the simulation results show that the method is simple and effective.

networked control systems(NCSs); time-varying sampling period; interval systems; guaranteed cost control

2016-05-20

辽宁省博士启动基金项目(20141069)

李媛(1974-)，女，山东龙口人，副教授，博士，主要从事网络控制的研究.

2095-2198(2016)04-0378-07

10.3969/j.issn.2095-2198.2016.04.018

TP273

A