基于粒子群优化算法的非线性控制系统参数优化
2016-02-07王功明袁德成
王功明, 袁德成
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
基于粒子群优化算法的非线性控制系统参数优化
王功明, 袁德成
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
针对反馈线性化策略中补偿器参数与实际受控对象参数发生失配的情况,提出一种基于粒子群优化算法求解实际系统参数的方法.以补偿器与受控对象参数完全匹配为参考系统,将施加在实际系统的激励信号同样施加在这个参考系统上,对两者的输出加以比较,进一步构造参数优化问题.决策变量是受控对象中发生变化的参数集,目标函数是两者输出之差的最小累加和,约束条件包括决策变量的上下限、系统的模型以及外部控制器等.采用粒子群优化算法求解这个非线性规划问题,所得决策变量的最优值即为当前实际受控系统参数的真实值.大量仿真计算表明,粒子群优化算法能够求出较为精确的实际系统参数值,并实现补偿器参数与实际受控对象参数之间的重新匹配.
等效线性化失配; PSO算法; 参考系统; 参数优化
在非线性系统的各类控制策略中,基于反馈线性化的控制算法是重要的一类.反馈线性化的基本思想是通过利用间接的状态观测器信息或直接的状态测量信息,构造非线性补偿环节,然后将其加在非线性受控对象之前,形成一个补偿器和受控对象串联在一起的新对象.这样就将一个非线性控制系统控制设计问题转变成线性控制系统问题,然后可以运用各种成熟的线性控制理论和方法.然而,反馈线性化控制策略中遇到一个主要问题——鲁棒性问题,即当补偿器设计中用到的模型结构或参数与实际受控对象的结构或参数不一致时,原来设计期望的等效线性关系就会失效,从而导致原设计的系统期望的鲁棒稳定性和鲁棒性能指标得不到保证.此问题在很大程度上影响和制约了这类先进控制策略的工程应用.在参数优化方面,LI Hongqi等利用CNOP方法研究了LSM参数化问题[1];QI Hongli结合人工神经网络和遗传算法研究了GECDS参数优化问题[2].而对于非线性特性反馈线性化中非线性补偿器和受控对象参数之间参数优化匹配的问题,由于非线性补偿器和受控对象中存在参数共享和高度非线性,以上方法显得无能为力.针对此问题,本文提出一种基于粒子群优化算法估计实际受控对象参数变化的新方法,根据系统实际情况构造参数优化问题,通过大量仿真计算表明,基于粒子群优化算法估计实际受控对象参数变化的方法能够较为准确地求出满足相关目标函数要求的最优参数解.
1 问题描述
在反馈线性化控制策略中,针对实际受控对象参数发生变化而使原设计期望的等效线性关系失效的情况,引入基于参考模型[3]的参数优化建模思想.当受控对象参数发生变化时,利用有效的优化方法通过控制性能指标不断逼近受控对象实际参数值,只要性能指标达到足够精准的程度,必然能够找到受控对象实际参数值.控制结构如图1所示,d为已知扰动.
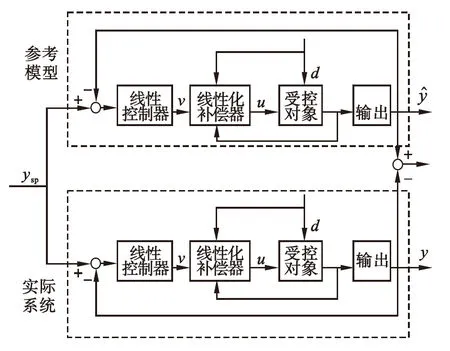
图1 参数优化控制结构
Fig.1 Parameters optimization control structure diagram
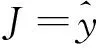
(1) 在实际受控对象的设定值上增加测试信号ysp,在线记录系统输出y.
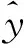
(3) 构造最优问题.
性能指标:
(1)
约束条件:
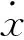
(2)
(3)
(4)
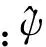

(6) 调整实际系统中线性化补偿器中的对应参数.
本文以粒子群优化算法为例展开讨论.
2 粒子群优化算法
2.1 算法原理
粒子群优化算法[4](Particles Swarm Optimization,即PSO算法)是一种基于不断迭代进化的计算技术,初期是针对鸟类捕食行为的研究.PSO算法也是一种基于迭代原理的优化工具,系统首先设置为一组随机解,通过模拟类似小鸟捕食的原理进行迭代搜寻最优值.在PSO算法中,每个优化问题的解均对应于搜索空间中的一只小鸟,每只小鸟均被抽象为没有质量和体积的“粒子”(Particle),并且将其延伸至N维空间中,粒子i在N维空间里的位置表示为一个矢量,同样的,每个粒子的飞行速度也表示为一个矢量.所有的粒子都有一个由被优化的函数所决定的适应值(fittness),每个粒子都有由速度决定它们飞翔的方向和距离.在连续迭代寻优的过程中,所有粒子将每次迭代所寻找到的优化解保存起来,然后根据所期望的优化要求将保存起来的优化解进行比较,这样每个粒子就知道自己到目前为止所发现的最好位置(pbest)和当前的位置,这个便可以看作是粒子自己的飞行经验.同样的,通过所有粒子之间的位置比较,每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest,gbest是pbest中的最优解),这个便可以看作是粒子同伴之间的飞行经验.粒子就是通过自己的飞行经验和同伴中最好的飞行经验来决定下一步的飞行运动.
PSO算法首先设置为一组随机解,即初始化,然后粒子们就追随当前的最优粒子在解空间中搜索.具体来说,假设d维搜索空间中第i个粒子的位置和速度分别为Xi=(xi,1,xi,2,…,xi,d)和Vi=(vi,1,vi,2,…,vi,d),那么在每一次迭代寻优中,粒子通过跟踪这两个最优解不断更新自己的两个信息;第一个就是粒子本身所找到的最优解,即个体极值pbest,Pi=(pi,1,Pi,2,…,pi,d);另一个是整个种群目前为止所找到的最优解,即全局最优解gbest,Pg=(pg,1,pg,2,…,pg,d).在找到这两个最优解后,粒子将根据式(5)和式(6)更新自己的速度和位置[5].
vi,j(t+1)=wvi,j(t)+c1r1[pi,j-
xi,j(t)]+c2r2[pg,j-xi,j(t)]
(5)
xi,j(t+1)=xi,j(t)+vi,j(t+1)
j=1,2,…,d
(6)
其中:w为惯性权重;d为待优化问题解的维度;c1和c2为正的学习因子;r1和r2为介于0到1之间均匀分布的随机数.粒子移动搜索的原理如图2所示.
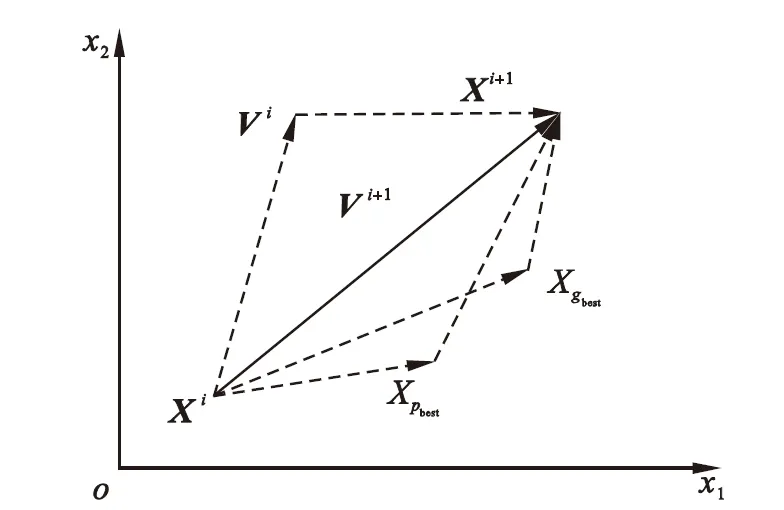
图2 粒子移动原理
Fig.2 Schematic diagram of particles move
PSO算法的求解实质上是不断迭代与寻优的过程,其运行时间主要取决于粒子种群数、迭代次数、待优化参数的上下限以及目标函数的复杂程度等因素.
2.2 算法步骤
PSO算法的求解是根据待优化问题按照既定步骤不断寻优的过程,其步骤如下:
(1) 随机初始化粒子群体的位置和速度.
(2) 计算每个粒子的适应值.
(3) 针对每个粒子,将其适应值与个体极值进行比较,如果较优,则更新当前的个体极值.
(4) 针对每个粒子,将其适应值与全局极值进行比较,如果较优,则更新当前的全局极值.
(5) 根据式(5)和式(6),更新每个粒子的位置和飞行速度.
(6) 如果没有满足预先设定的停止准则(通常情况下设置为最大迭代次数),则返回步骤(2),如果满足则停止程序运算.
在MATLAB环境中,PSO算法主程序运行后,将返回待求优化参数的最优解,以及最优解所对应的适应度.PSO算法运算流程如图3所示.
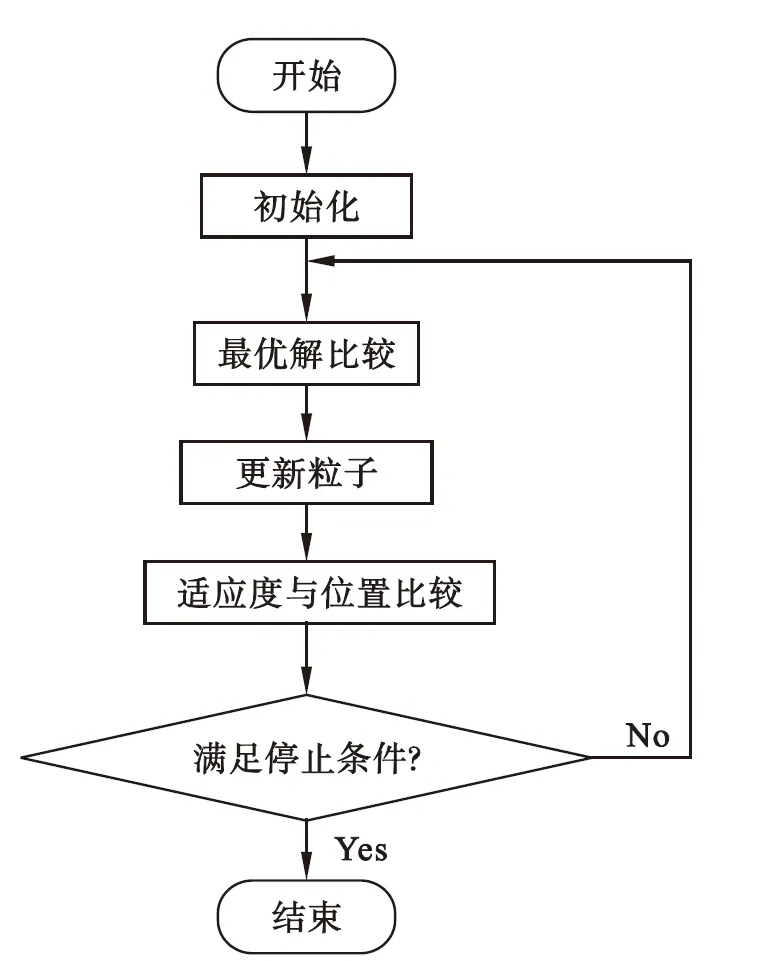
图3 PSO算法流程
Fig.3 PSO algorithm flow chart
3 仿真实例
以连续聚合反应过程为例[6],其数学模型表述为:
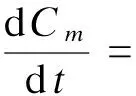
(7)
(8)
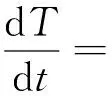
(9)
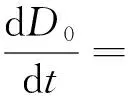
(10)
(11)
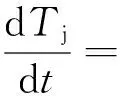
(12)
其中:
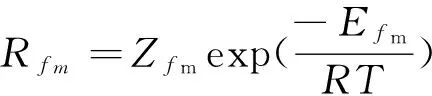
P0(CI,T)=

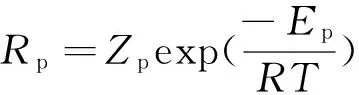
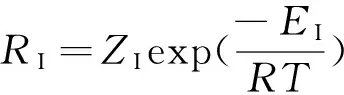
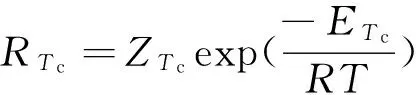
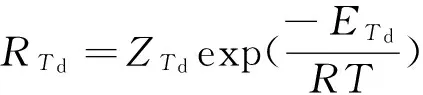
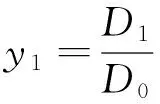
x1=Cm,x2=CI,x3=T,x4=D0,x5=D1,x6=Tj分别表示输入单体摩尔浓度、催化剂摩尔浓度、反应器温度、废弃单体摩尔浓度、废弃单体质量浓度和夹套温度,具体参数见文献[6].首先运用反馈线性化[6]方法设计线性补偿器,然后外部应用PID控制器(KP=0.1,KI=1.33,Kd=0).在这个受控对象模型中,有许多参数存在不确定性,例如传热系数、反应物密度ρ及反应速度前置常数Z,这些不确定性都会导致原设计的等效线性关系失效.在控制器设计时,假设知道这些存在不确定性参数的标称值以及其变化范围,那么寻优问题实质就是通过仿真确定其当前取值.
不确定性参数ψ的标称值及其容许变化范围如下:
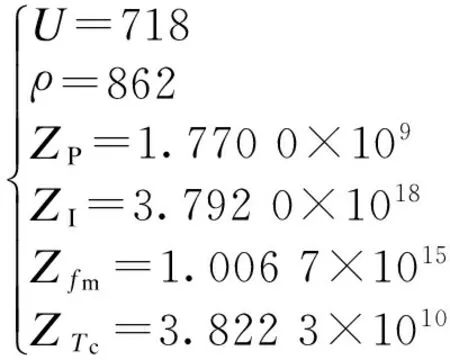
范围变化

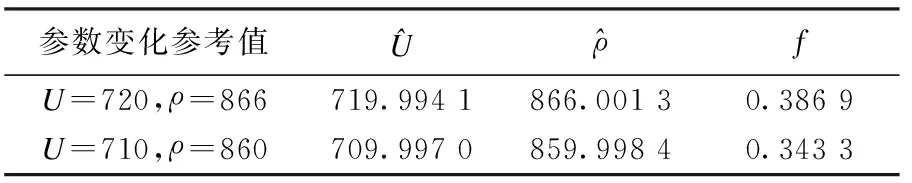
表1 PSO算法在不同U、ρ变化值时的最优解

表2 PSO算法在不同ZP、ZI变化值时的最优解

表3 PSO算法在不同Zfm、ZTc变化值时的最优解
由表1、表2和表3可以看出:当实际受控对象模型中不确定性参数在容许的范围内发生变化时,运用PSO算法能够求出较为接近参数当前取值的最优解,此时所求得的最优解可以近似看作等于参数当前取值.此外,通过研究PSO算法程序运算原理可知,不断的调节PSO算法运行程序中的内部参数[9],可以取得更佳的参数优化效果.
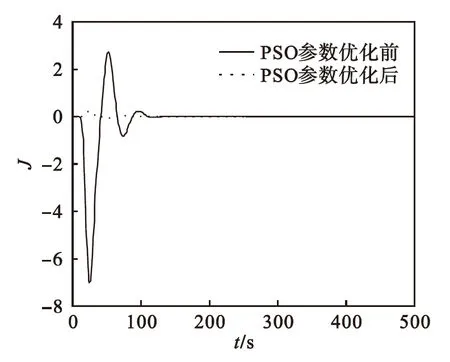
图4 不同U、ρ取值下PSO优化求解前后系统输出误差
Fig.4 Output error in different values ofUandρbefore and after optimization
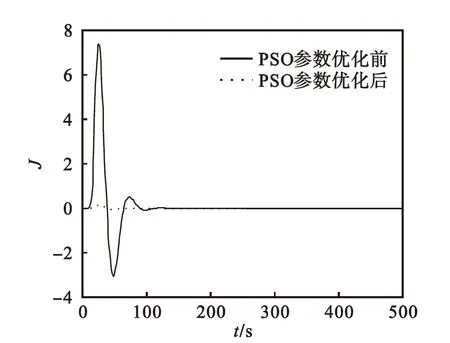
图5 不同ZP、ZI取值下PSO优化求解前后系统输出误差
Fig.5 Output error in different values ofZPandZIbefore and after optimization
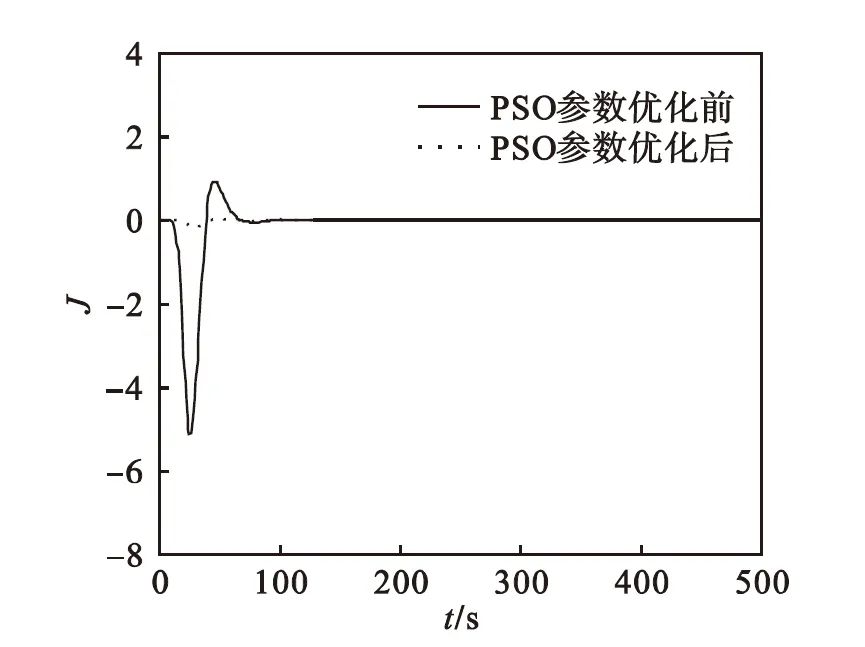
图6 不同Zfm、ZTc取值下PSO优化求解前后系统输出误差
Fig.6 Output error in different values ofZfmandZTcbefore and after optimization

4 结束语
针对非线性系统反馈线性化中实际受控对象参数发生变化而使原设计期望的等效线性关系失效的情况,构造参数优化问题,提出并应用PSO算法估计实际系统真实参数的方法.大量仿真数据表明,基于PSO算法估计实际系统真实参数的方法能够较为准确地估计出实际系统的真实参数值,具有较大的实际应用价值.文中分析主要限于实际系统参数在安全范围内变化的情况,将研究扩展到实际系统参数变化超出安全范围的情况下如何估计其真实值的问题将是今后要开展的工作.
[1] LI H Q,GUO W D,SUN G D,et al.A New Approach for Parameter Optimization in Land Surface Model [J].Advances in Atmospheric Sciences,2011,28(5):1056-1066.
[2] QI H L,ZHAO H,LIU W W,et al.Parameters Optimization and Nonlinearity Analysis of Grating Eddy Current Displacement Sensor Using Neural Network and Genetic Algorithm [J].Journal of Zhejiang University SCIENCE A,2009,10(8):1205-1212.
[3] 师佳,江青茵,曹志凯,等.基于2维性能参考模型的2维模型预测迭代学习控制策略[J].自动化学报,2013,39(5):566-572.
[4] 龚纯,王正林.精通MATLAB最优化计算[M].2版.北京:电子工业出版社,2011:270-275.
[5] GAING Z L.A Particle Swarm Optimization Approach for Optimum Design of PID Controller in AVR System [J].IEEE Transactions on Energy Conversion,2004,19(2):384-391.
[6] DAOUTIDIS P,SOROUSH M,KRAVARIS C.Feedforward/Feedback Control of Multivariable Nonlinear Processes[J].AIChE,1990,36(10):1471-1484.
[7] SOLIHIN M I,TACK L F,KEAN M L.Tuning of PID Controller Using Particle Swarm Optimization[C]//ICASEIT.Kuala Lumpur:[s.n.],2011:458-460.
[8] 金翠云,王建林,马江宁,等.改进的PSO算法及其在PID控制器参数整定中的应用[J].电子测量与仪器学报,2010,24(2):141-146.
[9] WEI X Y,PAN H X,HUANG J Y.Application of Particle Swarm Optimization to Fault Condition Recognition Based on Kernel Principal Component Analysis[J].International Journal of Plant Engineering and Management,2009,14(3):130-134.
[10]HINICH M J.Testing for Gaussianity and Linearity of a Stationary Time Series[J].Journal of Time Series Analysis,1982,3(3):169-176.
[11]CAI S J,WANG P,LI L H,et al.Higher-order Principal Component Pursuit via Tensor Approximation and Convex Optimization [J].Journal of Systems Engineering and Electronics,2014,25(3):524-529.
[12]KUMARDAMARLA S,KUNDU M.Control of Yeast Fermentation Bioreactor in Subspace[J].International Journal of Computer Applications,2013,64(5):13-18.
Nonlinear Control System Parameter Optimization Based on Particle Swarm Optimization Algorithm
WANG Gong-ming, YUAN De-cheng
(Shenyang University of Chemical Technology, Shenyang 110142, China)
A kind of solving practical system parameter method based on the particle swarm optimization algorithm is presented for the case where there is mismatch between compensator parameters and practical system parameters in feedback linearization.The complete matching between compensator parameters and practical system parameters is treated as reference system,excitation signal is posed onto practical system and reference system simultaneously,and their outputs are put into contrast,then optimization problem can be structured.Decision variables are changeable parameters,the objective function is minimum sum of the difference between their outputs,constraint condition includes the bound of decision variables,system model and external controller and so on.This nonlinear programming problem can be solved by using the PSO method,and the optimal solutions are the practical system parameters real values,a mass of simulation calculations show that the PSO algorithm can calculate more accurate practical system parameters values,and bring the matching again between compensator parameters and practical system parameters.
equivalent linearization mismatch; PSO algorithm; reference system; parameter optimization
2014-10-13
王功明(1987-),男,山东莒县人,硕士研究生在读,主要从事复杂工业过程建模与控制研究.
袁德成(1960-),男,内蒙古阿拉善人,教授,博士,主要从事化工过程建模、控制与优化的研究.
2095-2198(2016)04-0356-06
10.3969/j.issn.2095-2198.2016.04.014
TP273
A
