基于滑模控制的分数阶超混沌系统投影同步
2016-02-07颜闽秀罗铁军
颜闽秀, 罗铁军
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
基于滑模控制的分数阶超混沌系统投影同步
颜闽秀, 罗铁军
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
研究了一类分数阶超混沌系统的投影同步问题.利用分数阶性质及分数阶稳定理论,设计滑模控制器,实现分数阶超混沌系统的投影同步.并利用Lyapunov稳定理论证明误差系统的渐近稳定,数值仿真结果验证了控制器的有效性.
分数阶; 超混沌系统; 投影同步; 滑模控制
分数阶微积分有着悠久的发展历史,由于一直没有找到应用背景而未得到广泛的关注.近几十年来,学者研究发现许多物理过程中出现分数阶动力学行为[1],分数阶微积分的研究得到重视.自1990年Pecora和Carroll提出了混沌同步的定义并在电路中应用以来,混沌系统及其同步研究一直是热点.迄今为止,学者们提出多种同步方案,如完全同步[2]、反同步[3]、投影同步[4]、相同步[5]、广义同步[6]等.同时,多种实现混沌同步的方法相继提出,如观测器同步法[7],主动控制法[8],自适应同步法[9],滑模变结构同步法[10]等.其中,滑模变结构控制方法因其具有较强的抗干扰能力和鲁棒性,得到人们广泛的关注.超混沌系统通常被定义为具有多个正的Lyapunov指数的混沌系统[11-12].与低维混沌系统相比,由于其具有更复杂的动力学行为,更适合应用在安全通信[13].迄今为止,关于超混沌系统的研究较少,特别是关于分数阶超混沌系统的同步更是各国学者研究的一个热点课题[14-15].
本文针对一类分数阶超混沌系统的同步问题,设计滑模控制器,实现分数阶超混沌系统的投影同步.最后利用Lyapunov稳定性理论和数值算例证明该控制器的有效性.
1 分数阶微积分概述
1.1 分数阶微积分的定义
分数阶微积分在现代科学中起着重要作用,它能准确描述实际的物理模型.有关分数阶微分的定义很多,常用为[6]:
(1)
其中:m=[α],即m是第一个不小于α的整数;xm是通常意义上的m阶导数;Jβ(β>0)是β阶Reimann-Liouville积分算子.具体形式如下:
(2)
其中Γ代表Gamma函数.
1.2 分数阶微积分的一些性质
分数阶微积分的性质如下[1-3]:
性质1: 相加指数法则.
(3)
性质2: Caputo分数阶导数算子是线性算子.
(λ、μ是实常数)
(4)
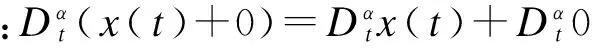
性质3: Caputo分数非线性系统,f(x(t))中x满足Lipschitz条件,即:
‖f(x1(t))-f(x2(t))‖≤
l‖x1(t)-x2(t)‖
(5)
其中l是正数,不失一般性,当x=0时有下式成立:
‖f(x1(t))‖≤l‖x1(t)‖,即
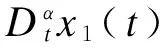
(6)
2 滑模控制器设计
考虑如下n维超混沌系统的驱动系统:
Dαx=Ax+f(x)
(7)
其中:0<α<1;x∈Rn为系统状态变量;A∈Rn×n为系统的线性部分;f(x)∈Rn为系统的非线性部分.
定义响应系统:
Dαy=By+g(y)+u
(8)
其中:0<α<1;y∈Rn为系统状态变量;B∈Rn×n为系统的线性部分;g(y)∈Rn为系统的非线性部分;u∈Rn为控制器.
定义误差系统:
e=y-lx
(9)
将(7)式、(8)式代入(9)式,可得误差系统:
Dαe=By-lAx+g(y)-lf(x)+u
(10)
利用加在响应系统上的控制器,实现驱动系统和响应系统的同步,即:
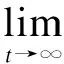
(11)
根据滑模控制的思想,可以设计滑模面:
S=Dα-1e
(12)
其中:S=(S1,S2,…,Sn)T;e=(e1,e2,…,en)T.
当系统在滑模面上运动时,误差系统满足[17-18]:
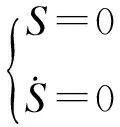
(13)
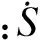
u=-(g(y)-lf(x))-(B-A)y+kξ-msign(S)
(14)
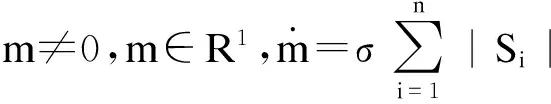
定理: 对于同步误差系统(10),在控制器u的作用下,能够实现超混沌系统的投影同步.
证明: 选取一个正定的函数:
(15)
则V(x)对时间t求导得
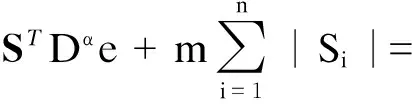
(16)
3 仿真算例
为了验证本文控制器的有效性,这里选取超混沌Chen系统为例进行研究.
超混沌Chen系统的方程为:
(17)
其中:a=35,b=7,c=12,d=3,r=0.5.当α=0.95时分数阶超混沌Chen系统的吸引子如图1所示.
图1 α=0.95时分数阶Chen超混沌吸引子
Fig.1 α=0.95Fractional-orderChenHyperchaoticattractor
驱动系统为:
(18)
其中:

响应系统为:
(19)
其中:

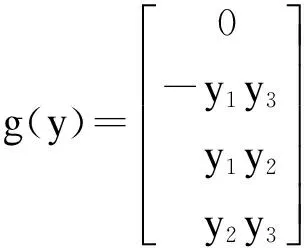
同步误差系统:
(20)
控制器:
msign(S)
(21)
在仿真中,驱动系统的初始值为(x1(0),x2(0),x3(0),x4(0))T=(2,0,1,-2)T,响应系统的初始值为(y1(0),y2(0),y3(0),y4(0))T=(10,5,21,-2)T,l=1.05,m=0.01.仿真结果如图2~图3所示.图2是在控制器作用下,同步误差的状态响应曲线.显然,在控制器的作用下同步误差系统渐近趋于0.图3是在本文设计的控制器作用下,驱动和响应系统的状态曲线.由图3可看出,响应系统能够跟随驱动系统,取得很好的同步效果.
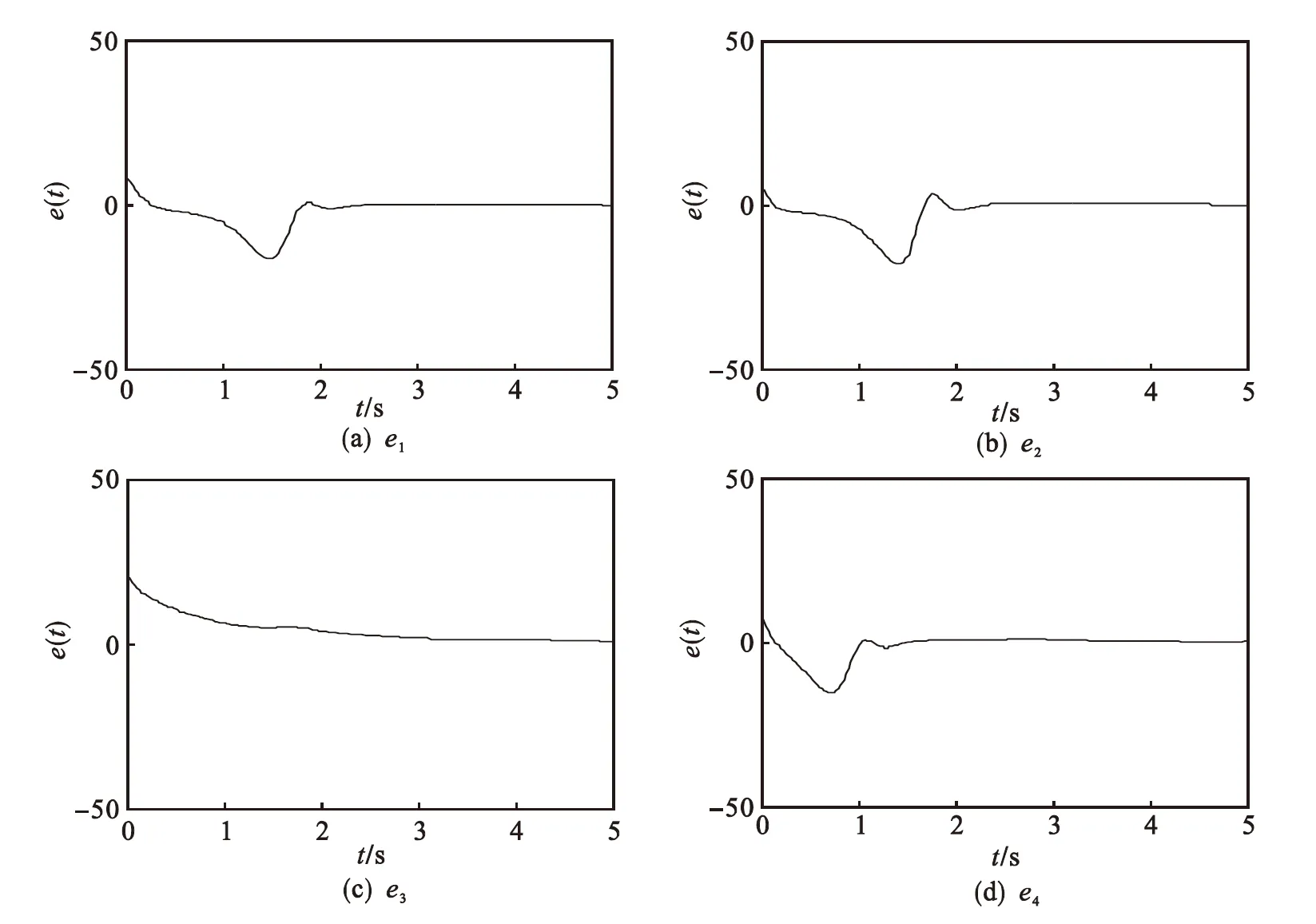
图2 系统误差状态曲线
Fig.2Systematicerrorstatecurve
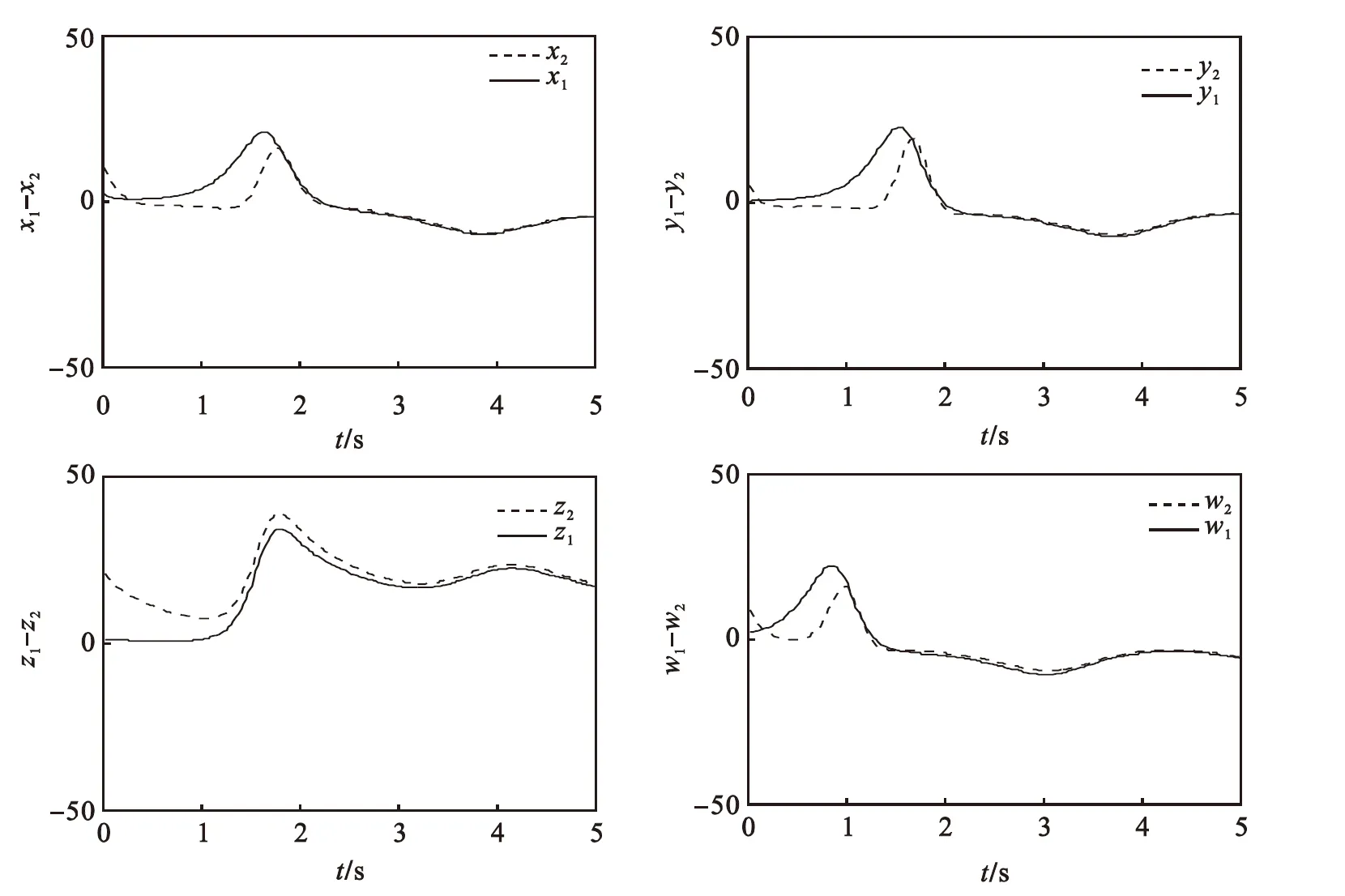
图3 系统同步状态曲线
Fig.3Systemsynchronizationstatecurve
4 总 结
本文主要研究了分数阶超混沌系统的投影同步问题,根据分数阶性质及分数阶稳定理论和Lyapunov稳定理论,设计了滑模控制器,实现了分数阶超混沌系统的投影同步,并将该方法应用于分数阶超混沌Chen系统,通过仿真算例验证了所提控制器的有效性.
[1] 刘崇新.分数阶混沌电路理论及应用[M].西安:西安交通大学出版社,2011:10-42.
[2] 徐春梅.几种典型混沌系统的同步研究[D].哈尔滨:哈尔滨工业大学,2013:4-11.
[3] 张若洵.分数阶微分非线性系统的稳定性理论及在混沌同步中的应用研究[D].石家庄:河北师范大学,2012:4-21.
[4] 蔡娜,井元伟,张嗣瀛.不同结构混沌系统的自适应同步和反同步[J].物理学报,2009,58(2):802-813.
[5] 高铁杠,陈增强,袁著祉.基于观测器的混沌系统的同步研究[J].物理学报,2004,53(5):1305-1308.
[6] 张健,徐红兵,张洪斌.基于观测器的一类连续非线性系统的采样控制[J].自动化学报,2010,36(12):1780-1787.
[7] 闵富红.混沌系统同步控制的有关问题研究[D].南京:南京理工大学,2007:6-18.
[8] 赵琰,张化光.基于T-S模糊模型的Nadolschi混沌系统同步控制[J].清华大学学报(自然科学版),2007,47(S2):1778-1781.
[9] 颜闽秀,郑小帆.基于主动自适应滑模控制的超混沌系统同步[J].沈阳大学学报(自然科学版),2014,26(6)479-485.
[10]孙宁,张化光,王智良.基于分数阶滑模面控制的分数阶超混沌系统的投影同步[J].物理学报,2011,60(5):126-132.
[11]刘福才,李俊义,臧秀凤.基于自适应主动及滑模控制的分数阶超混沌系统异结构反同步[J].物理学报,2011,60(3):108-117.
[12]白敬.分数阶混沌系统的滑模控制[D].北京:北京交通大学,2012:16-36.
[13]ZHANGRX,YANGSP.RobustSynchronizationofTwoDifferentFractional-orderChaoticSystemswithUnknownParametersUsingAdaptiveSlidingModeApproach[J].NonlinearDynamics,2013,71(1):269-278.
[14]AGHABABAMP.ANovelTerminalSlidingModeControllerforaClassofNon-autonomousfractional-orderSystems[J].NonlinearDynamics,2013,73(1):679-688.
[15]LÜL,YUM,LICR,etal.ProjectiveSynchronizationofaClassofComplexNetworkBasedonHigh-orderSlidingModeControl[J].NonlinearDynamics,2013,73(1):411-416.
[16]王乃洲.基于分数阶微积分理论的滑模变结构控制[D].南京:南京林业大学,2010:5-35.
[17]WANGXY,ZHANGXP,MAC.ModifiedProjectiveSynchronizationofFractional-orderChaoticSystemsviaActiveSlidingModeControl[J].NonlinearDynamics,2012,69(1):511-517.
[18]CHENDY,ZHANGRF,MAXY,etal.ChaoticSynchronizationandAnti-synchronizationforaNovelClassofMultipleChaoticSystemsviaaSlidingModeControlScheme[J].NonlinearDynamics,2012,69(1):35-55.
liding Mode Control for Projective Synchronization ofFractional-order Hyperchaotic Systems
YANMin-xiu,LUOTie-jun
(ShenyangUniversityofChemicalTechnology,Shenyang110142,China)
Projectivesynchronizationoffractional-orderhyperchaoticsystemsisstudiedhere.Accordingtothepropertiesandstabletheoremoffractionalequation,slidingmodecontrollerisdesignedtoachievetheprojectivesynchronizationoffractional-orderhyperchaoticsystems.Moreover,theglobalasymptoticstabilityoftheerrordynamicsisderivedintheLyapunovsense.Simulationstudieshaveshowntheproposedcontrollerscangetgoodcontroleffects.
fractional-order;hyperchaoticsystems;projectivesynchronization;slidingmodecontrol
2014-10-11
国家科技支撑计划项目(2012BAF09B01)
颜闽秀(1972-),女,福建仙游人,博士,副教授,主要从事变结构控制、智能控制领域的研究.
2095-2198(2016)04-0351-05
10.3969/j.issn.2095-2198.2016.04.013
TP273.2
A
