利用分数阶(G′G)展式法构造分数阶KdV-Burger方程方程的精确行波解

尹伟石，李琰，徐飞

（1.长春理工大学理学院，长春 130022；2.东北师范大学数学与统计学院，长春 130024）

利用分数阶(G′G)展式法构造分数阶KdV-Burger方程方程的精确行波解

尹伟石1，李琰1，徐飞2

（1.长春理工大学理学院，长春 130022；2.东北师范大学数学与统计学院，长春 130024）

(G′G)展式法是一种行之有效的求解分数阶偏微分方程的方法.利用行波变化与齐次平衡技巧可以对该方法进行拓展，拓展后的方法能够处理更一般的分数阶偏微分方程.最后将拓展后的方法应用到基于黎曼-刘维尔积分意义下的时间空间分数阶KdV-Burger方程中,通过符号计算可以得到方程的精确行波解。与其他方法相比,拓展的(G′G)展式法不需要进行变换和数值逼近,计算更加的简洁。

分数阶(G′G)展式法；分数阶KdV-Burger方程；精确行波解

近年来，分数阶偏微分方程（FPDEs）频繁地出现于物理、生物、工程、信号处理、系统识别、控制理论、金融和分子动力学等领域，已经成为偏微分方程领域关注的焦点问题。许多文章对FPDEs进行了研究，如在文献［1］中，Jafari等利用分数子方程方法构造分数阶Duffing模型和非线性Sharma-Tasso-Olver的精确行波解；Baleanu等利用不动点定理的方法研究了非线性分数阶微分方程边值问题解的存在性和唯一性［2］；Nyamoradi等给出分数阶多点边值问题的解的存在性［3］。

在分数阶微分方程的研究中，构造分数微分方程的精确解和数值解是一个重要的问题。目前，针对这一问题已经得到许多有效的求解方法，其中包括变分迭代法［4-6］、同伦摄动法［7］、微分变换法［8］、有限差分法［9］、有限元方法［10］等。本文在改进过的黎曼-刘维尔积分意义下，根据(G′G)展开法［11］构造一个新的分数阶子方程。该方法主要利用如下的分数阶常微分方程（ODE）：

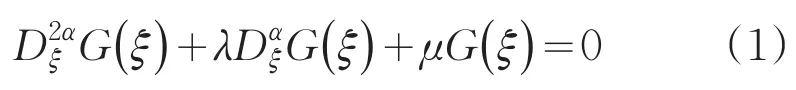
1 黎曼-刘维尔积分意义下的G′G的展开法

黎曼-刘维尔积分意义下函数的α阶导的定义：

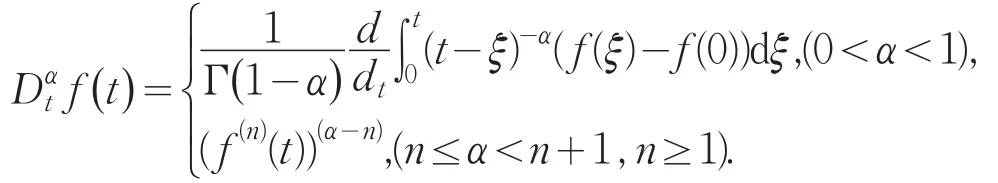
在上述导数意义下，函数具有如下性质：

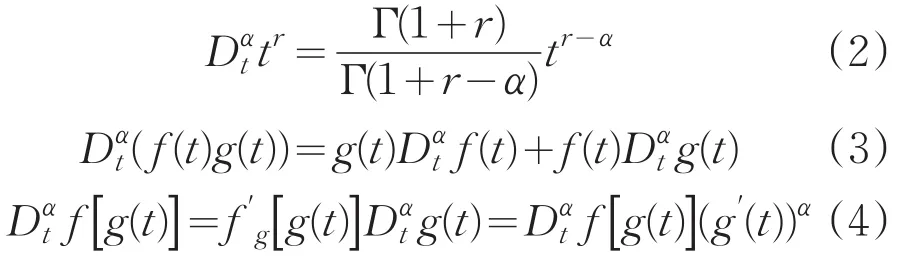
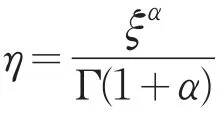
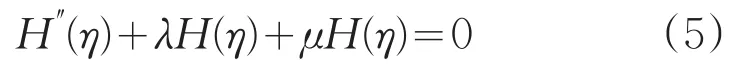
利用二阶常微分方程求解方法，可以得到式（5）的通解：

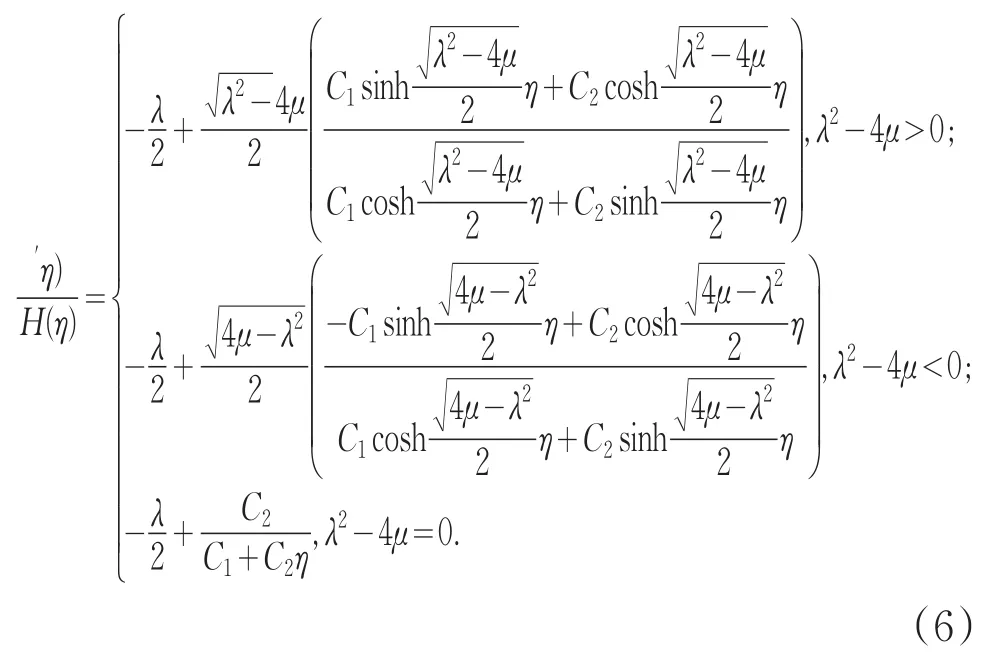
其中,C1,C2为任意非零常数且满足上述式子。利用上述性质中（2）和（4），则有，从而可得：

2 FPDEs的分数阶子方程法

考虑如下依赖于独立变量t,x1,x2,…,xn的分数阶偏微分方程，

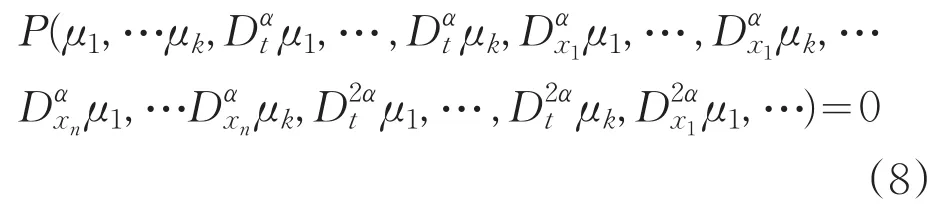
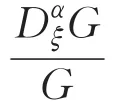
（1）假设

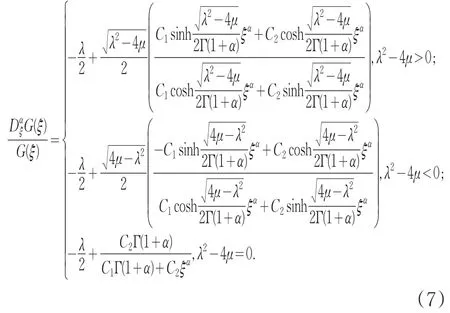
根据（4），可将（8）式被转化成为关于自变量ξ的FODEs：

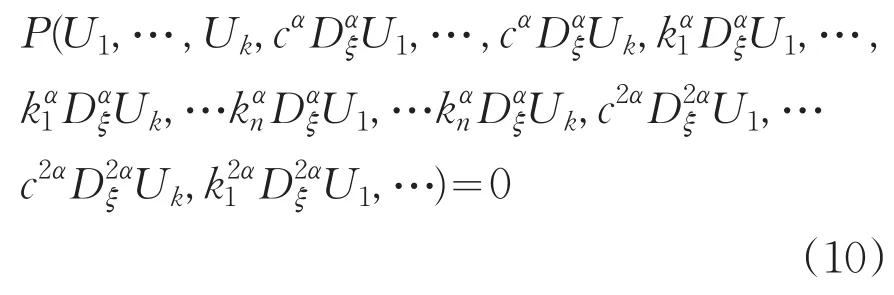
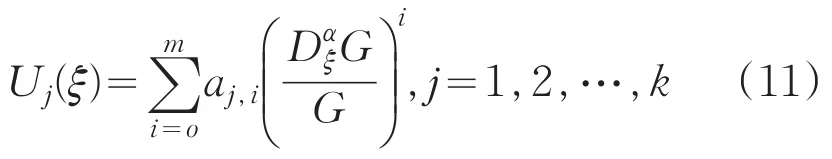
其中，G=G(ξ)且满足（1）式，aj,i,i=0,1,…,mi, j=1,2,…,k,为多项式的系数，且最高次项aj,m≠0。这里的最高次数正整数m可以通过（10）式中出现的非线性项与最高阶导数项相互保持齐次平衡来确定。

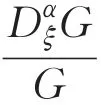
3 应用举例

考虑如下的时间-空间分数阶KdV-Burger方程

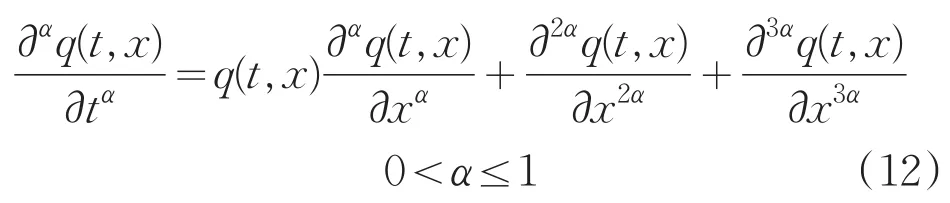
在（12）里，为了求解上述方程的精确解，在（11）中采用的是求解Riccati方程的方法，由于一般的Riccati方程式不可解的，那么只能利用特殊形式的Riccati方程的解。为避免出现Riccati方程不可解的问题，利用本文中的方法进行求解上述时间-空间分数阶KdV-Burger方程精确形式行波解。

根据（2）-（4）式中分数阶导数性质，方程（12）式可转化为：

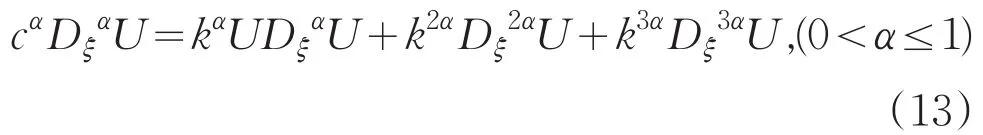
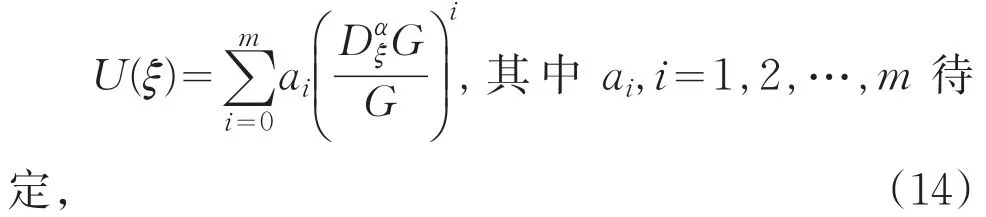
且G=G(ξ)满足（1）式，平衡（13）式非线性项和最高阶导数项，即UDαξU和D3ξαU，即m+m+1=m+3，从而可以得到最高次数m=2.故

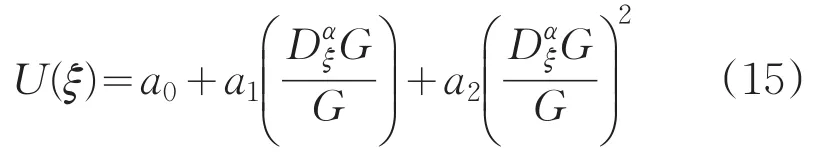
对（15）式求各阶导数，并利于（1）则可得到

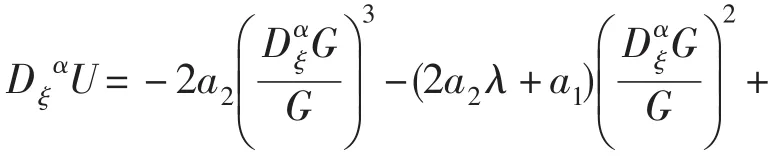
012一组代数方程.

化简后将a2代入上式求得：

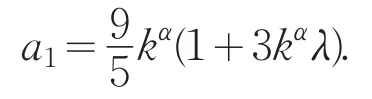
将a2，a1代入上式可以得到：

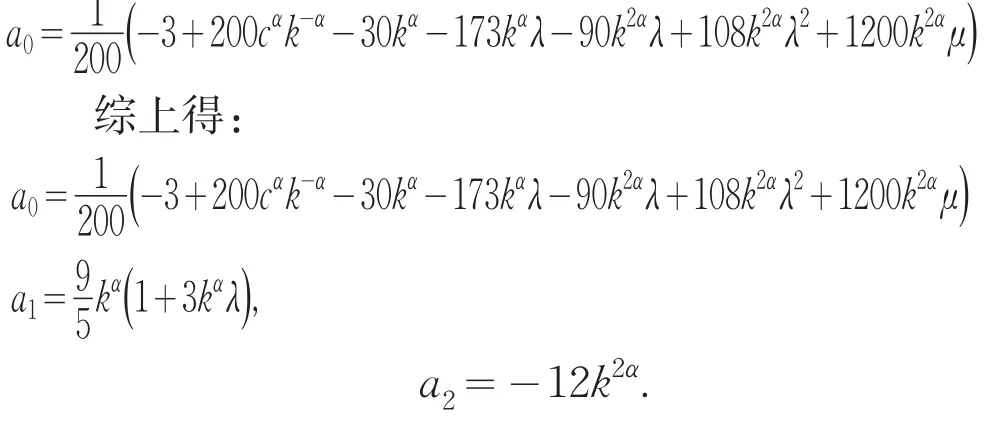
将上式代入（15），再通过（7）就可以得到原来问题的精确解：

当λ2-4μ＞0时，

当λ2-4μ＜0时，

当λ2-4μ=0时，

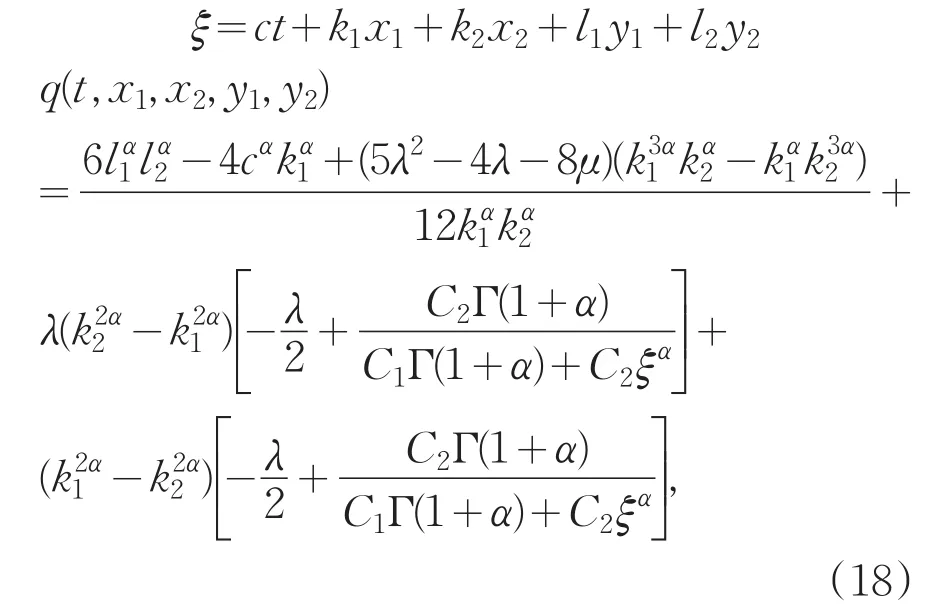
其中，C1，C2为任意非零常数且满足上述式子有意义。综上可以得到（16）、（17）、（18）均为原分数阶偏微分方程的精确形式的行波解。

［1］Jafari H，Tajadodi H，Baleanu D，et al.Fractional sub-equation method for the fractional generalized reactionDuffingmodelandnonlinearfractional Sharma-Tasso-Olver equation［J］.Central European Journal of Physics，2013，11（10）：1482-1486.

［2］Baleanu D，Rezapour S，Mohammadi H.Some existenceresultsonnonlinearfractionaldifferential equations［J］.PhilosophicalTransactionsofThe Royal Society A-Mathematical Physical and Engineering Sciences，2013（371）：1-7.

［3］Nyamoradi N，Baleanu D，Agarwal R P.On a Multipoint Boundary Value Problem for a Fractional Order Differential Inclusion on an Infinite Interval［J］. Advances in Mathematical Physics，2013（2）：194-201.

［4］HE Ji-huan.A New Approach to Nonlinear Partial Differential Equations［J］.Communications in Nonlinear Science&Numerical Simulation，1997，2（4）：230-235.

［5］Wu Guo-cheng，Lee E W M.Fractional variational iteration method and its application［J］.Physics Letters A，2010，374（25）：2506-2509.

［6］Jafari H，Tajadodi H.He’s variational iteration method for solving fractional Riccati differential equation［J］.InternationalJournalofDifferentialEquations，2010：1-8.

［7］Jafari H，Momani Sh.Solving fractional diffusion and wave equations by modified homotopy perturbation method［J］.Physics Letters A，2007，370（5-6）：388-396.

［8］Odibat Z，Momani S.Fractional Green function for lineartime-fractionalequationsoffractionalorder［J］.Journal of Applied Mathematics and Computing，2007，24（1）：167-178.

［9］Cui Ming-rong.Compact finite difference method for the fractional diffusion equation［J］.Journal of Computational Physics，2009，228（20）：7792-7804.

［10］Huang Quanzhong，Huang Guanhua，Zhan Hongbin. A finite element solution for the fractional advection-dispersion equation［J］.Advances in Water Resoucesr，2008，31（12）：1578-1589.

［11］Wang，ML，Li，XZ，Zhang，JL：The expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics［J］.Phys. Lett.A，2008（372）：417-423.

［12］Bekir A，Güner Ö.The-expansion method using modifiedRiemann-Liouvillederivativeforsome space-time fractional differential equations［J］.Ain Shams Engineering Journal，2014，5（3）：959-965.

Construction of Exact Traveling Solutions of Fractional KdV-Burger Equation Using the Fractional(G′G)Method

YIN Weishi1，LI Yan1，XU Fei2
（1.School of Science，Changchun University of Science and Technology，Changchun 130022；2.Mathematics and Statistics，Northeast Normal University，Changchun 130024）

(G′G)expansionmethod is an effective method for solving fractional partial differentialequations.The method can be extended by using the traveling wave variation andthe homogeneous balance technique，and the extended method can be used to dealwith the more general fractional partial differential equations.Finally，theextended method is applied to the time space fractional KdV-Burger equationbased on the Liu Weier Riemann integral，and the exact traveling wave solutionsof the equations can be obtained by the symbolic computation.Compared withother methods，(G′G)expansionmethod don’t need to doing transform and numerical approximation，so thecalculation is more simple.

fractional(G′G)method；fractional KdV-Burger equation；exact traveling wave solutions.

O241.82

A

1672-9870（2016）05-0125-04

2016-03-31

国家级大学生创新创业训练计划项目（201510200028）

尹伟石（1980-），博士，讲师，E-mail：yinweishi@foxmail.com