基于连接矩阵的移动Ad Hoc网络可靠性评估方案*

赵 荷， 盖 玲

(1.成都东软学院 计算机科学与技术系，四川 成都 611844;2.上海大学 管理学院，上海 200444)



基于连接矩阵的移动Ad Hoc网络可靠性评估方案*

赵 荷1*， 盖 玲2

(1.成都东软学院 计算机科学与技术系，四川 成都 611844;2.上海大学 管理学院，上海 200444)

移动Ad Hoc网络(MANET)的动态拓扑结构使网络可靠性评估较为困难，为此提出一种基于连接矩阵的MANET可靠性评估方案.首先，确定网络中的源-终节点对和中继节点.然后，根据节点间欧式距离和通信范围来检测中继链路状态，并构建连接矩阵.最后，根据连接矩阵判断网络连接性，以多轮连接性的均值作为网络的最终可靠性.仿真实验中，评估了节点移动模型、网络大小、节点数量和通信范围对网络可靠性的影响，能够为网络设计者提供有力的依据.

移动Ad Hoc网络；网络可靠性；连接矩阵；节点移动模型

移动Ad Hoc网络(Mobile Ad Hoc Network, MANET)是一种新型的移动自组织网络[1].对于拓扑结构不断变化的MANET，网络的可靠性是构建网络时需要考虑的一个重要指标[2]，MANET中，节点间的链接是影响网络可靠性的一个重要因素，而高度动态特性使节点链接频繁地断裂或重建，已成为系统可靠性评估的一个挑战[3].对于MANET的可靠性计算，根据通信节点数量可分为2-终端、k-终端和全终端可靠性[4-5].其中，2-终端可靠性为一个特定节点对相互成功通信的概率.那么，网络的可靠性可定义为网络中每对节点相互成功通信的概率[6].目前，学者提出了多种MANET可靠性评估方法.例如，[7]提出了基于蒙特卡罗仿真的评估方法，考虑了随机路点移动模型，并使用横向优先搜索方法来检查网络中的连接.然而，该方法会随着网络尺寸的增加变得非常复杂，实用性不强.[8]识别网络中关键的链路，通过基于跳数的网络连接来计算MANET的网络可靠性.然而，该方案仅适用于跳数大于等于3时的场景.

本文提出了一种基于连接矩阵的MANET可靠性评估方法，以2-终端可靠性计算为基础，研究了随机路点移动(Random Waypoint Mobility, RWPM)和高斯-马尔可夫移动(Gauss-Markov Mobility, GMM)模型对可靠性的影响.另外，还分析了网络大小、节点数量和通信范围对网络可靠性的影响.为网络设计者进行可靠MANET的构建和参数设定提供有力的依据.

1 MANET网络模型

1.1 网络模型

给定一个具有n个移动节点(Mobile Node, MN)的MANET，在任意时刻τ时，都可以将该网络建模为一个固定的网络几何随机图G(U,L,τ).假设所有MN具备相等的传输范围rj，且失效时间遵循威布尔分布，则可以基于节点位置、节点距离和传输范围直接创建链路.

网络节点的失效时间可以遵循多种分布，如指数、正态或威布尔分布.其中，在系统建模中，威布尔分布已广泛用于作为组件的故障模式[9].所以，本文采用威布尔失效分布模式管理节点的失效时间.另外，由于RWPM模型、GMM模型在模拟节点移动模式中有着广泛应用[10]，所以本文选择这些模型.因此，对于MANET可靠性的评估，考虑了以下假设：

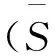
1.2 节点移动模型

1.2.1 随机路点移动模型(RWPM) 在RWPM模型中，节点i通过选择一个速度vi(τ)∈(Vmax,Vmin)和方向φi(τ)∈(0,2φ)移动到下一个目的地[11].利用(1)式来表示每个Δτ增量区间处，下一个节点的位置.

xi(τ+Δτ)=xi(τ)+Δτvi(τ)cosφi(τ)，yi(τ+Δτ)=yi(τ)+Δτvi(τ)sinφi(τ)．

(1)

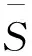
(2)

在上一时刻(τ-1)处的速度Sτ-1和方向φτ-1将影响当前的速度Sτ和方向φτ.MN的运动模式随着调优参数α而变化，当α=0时，MN的运动是完全随机的；当α=1时，MN的运动遵循之前运动方式，且进行直线运动.节点当前位置的表达式如下：

xτ=xτ-1+sτcos(φτ)，yτ=yτ-1+sτcos(φτ).

(3)

2 MANET可靠性评估方案

2.1 网络可靠性定义

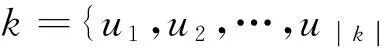
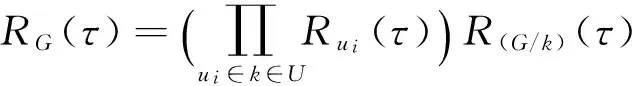
(4)

式中Rui(τ)表示节点链路正常传输的概率，定义如下：

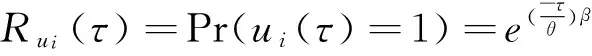
(5)

(6)

当中继节点对(ui,uj)之间的欧式距离dij(τ)在MN的传输范围内时，则链路存在.因此，链路状态Lij(τ)可定位为：

(7)

(8)

进一步地，在时刻τ，可以将所有中继节点对的链路状态构建成一个连接矩阵A(τ)，来表示网络连接性.A(τ)大小为n×n，元素为Lij(τ).利用连接矩阵A(τ)可以确定源-终节点对(s,t)之间的综合连接性.其中，第q次迭代中时刻τ时的网络连接性Cq(τ)状态定义如下：

(9)

在每个时间增量Δτ时，即节点位置变化时，利用连接矩阵A(τ)表征网络的连接性，一直持续到预定义的任务时间T.共执行Q次迭代，最后，将任务持续时间中的每个时间段τ处的仿真结果取平均值，来定义MANET的网络可靠性RG(τ)，定义如下：

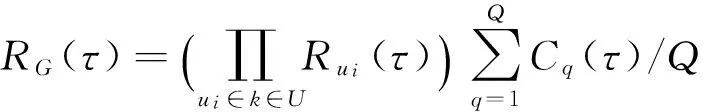
(10)

Var(RG(τ))=RG(τ)(1-RG(τ))/Q.

(11)

本文MANET可靠性评估方案分为2类，即不考虑节点移动性和考虑节点移动性的评估方案.

2.2 不考虑移动性时的可靠性评估方案

在不考虑移动性时，MANET中每个节点都具有固定的位置，根据网络中链路的连接性来评估网络可靠性，步骤如下：步骤1：初始化网络参数：n,D,T,rj,θ,β,Cq(τ)=0,Q.步骤2：对于i=1,2，…，n，生成节点的随机位置(xi,yi).步骤3：仿真节点状态，如式(6).步骤4：利用式(8)，确定每对MN之间的欧式距离.步骤5：利用式(7)，通过比较欧式距离和传输范围，检查链路的存在性.步骤6：利用τ时刻的连接矩阵检查网络的连接性，若已连接，则根据式(9)将Cq(τ)加1，并更新τ=τ+Δτ.步骤7：返回步骤4，直到τ=T.步骤8：迭代执行步骤2～步骤7，共执行Q次迭代.步骤9：利用式(10)和(11)计算RG(τ)和Var(RG(τ)).

2.3 考虑移动性时的可靠性评估方案

3 仿真实验

3.1 实验设置

使用Matlab2012工具，在配备Intel Core i5 CPU、2.00 GHz主频，Win7系统的PC机上执行算法.MANET网络中每个MN可以进行自组网连接，仿真工作72 h.实验中，根据分析需要，设置每个MN的传输范围rj为1～5 m， MN的移动速度为5 m/h，网络区域大小为100～1 600 m2的正方形区域，网络中的MN数量为10～100个，MN按照RWPM模型和GMM模型移动.另外，失效时间遵循威布尔分布，其中参数θ=1 000、β=1.5.对于随机度参数α(0≤α≤1)，本文设定α分别取值为0、0.5和1.

3.2 网络可靠性评估

对于具备RWPM、GMM移动模型和无节点移动的MANET网络，在不同网络区域大小、传输范围和节点数量下，分别利用提出的可靠性评估方法对网络链接可靠性进行评估.其中，为了区别RWPM模型，设定GMM模型中的α=0.5.在分类实验中，网络中默认设置20个MN，每个MN的传输范围为3 m，网络区域大小为400 m2.图1描述了不同网络区域大小下，网络的可靠性.可以看出，网络可靠性随覆盖区域的增大而大幅度下降.这是因为，网络变大，但节点数量和通信范围有限，致使一些节点间无法连接.另外，不同的移动模型导致不同的网络可靠性.其中，由于RWPM模型中节点无规则移动，导致一些节点会移动到边缘地带，从而无法连接，降低网络可靠性.在无移动场景中，初始阶段均匀分布，网络连接性较好.然而，当网络越来越大，即节点越来越稀疏时，相比于无移动场景，节点的移动性反而可以略微提高网络可靠性.这是因为，节点的移动可能会使部分节点移动到相对集中的区域，提高连接线.

图2描述了不同网络节点数量下网络的可靠性.可以看出，当节点密度增加但覆盖区域不变化时，可靠性有效增加.当高节点密度(U=100)被部署到一个400 m2的覆盖区域时，几乎所有场景中的节点都能和邻居节点相互连接，这使得网络更加稳定，其实际可靠性值近似达到了1.当低节点密度(U=10)被部署到一个400 m2的覆盖区域时，其实际可靠性值分别为0.427(RWPM模型)、0.452(GMM模型)、0.415(无移动性)，表明网络中只有小部分节点被连接起来. 另外，与上一个实验类似，不同的移动模型对网络可靠性具有一定的影响，且随着网络密度的不同而不同.

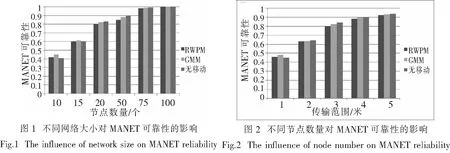
图3描述了不同传输范围下网络的可靠性.可以看出，网络可靠性随着节点传输范围的增加而单调增加.这是因为，随着传输范围增加，更多活跃的节点会被连接起来，使网络更稳定.但传输范围增加也会增加链路的传输能耗，所以可靠性会趋于稳定.图4描述了在整个作业持续时间内，在默认设置的网络中，各种移动模型下的网络可靠性变化趋势.可以看出，随着操作时间的增加，网络可靠性有所降低.这是因为，随着长时间的工作，有些节点可能出现故障，致使其无法与其他节点连接.另外，可以看出，不同的模型具有不同的网络可靠性.

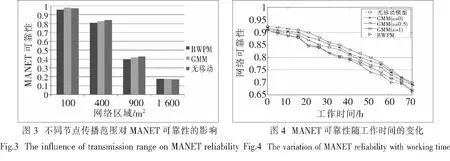
综上所有实验表明，节点的移动性对MANET连接可靠性的影响不是很大，而网络的大小、节点数和通信范围对可靠性影响较大.

4 结束语

该文提出一种基于网络中各节点间链接可靠性分析的MANET可靠性评估方法，在RWPM和GMM移动模型下，对具备不同的网络大小、节点数量和传输范围的网络进行可靠性评估.提出的方法计算简单，且可扩展为以k-终端或全终端可靠性为基础的网络可靠性评估，为网络设计者在参数选择时提供有效依据.

[1] 何晖, 王换招, 李昊,等. 增强Ad Hoc网络稳定性的移动问题解决策略[J]. 西安交通大学学报, 2011, 45(4): 6-11.

[2] 梁广民, 王健. 移动自组网中兼顾通信可靠性和链路长度的可信路由协议[J]. 南京大学学报:自然科学版, 2012, 48(2): 206-213.

[3] CHATURYEDI S K,PADMAVATHY N. The influence of scenario metrics on network reliability of mobile ad hoc network[J]. International Journal of Performability Engineering, 2013, 9(1): 61-74.

[4] PADMAVATHY N, CHATURVEDI S K. Evaluation of mobile ad hoc network reliability using propagation-based link reliability model[J]. Reliability Engineering & System Safety, 2013, 115(7):1-9.

[5] 邹青丙, 何明, 王琰,等. 无线多跳网络可靠性评估方法研究[J]. 计算机工程与应用, 2015, 51(5): 88-91.

[6] CHEN B, PHILLIPS A, MATIS T I. Two-terminal reliability of a mobile ad hoc network under the asymptotic spatial distribution of the random waypoint model[J]. Reliability Engineering & System Safety, 2012, 106(3):72-79.

[7] JASON L C, JOSE E R. Mobility and reliability modeling for a mobile ad hoc network[J]. Iie Transactions, 2012, 41(1):23-31.

[8] AHMAD M, KUMAR MISHRA D. A reliability calculations model for large-scale MANETs[J]. International Journal of Computer Applications, 2012, 24(9):17-21.

[9] 夏晓峰, 何常胜. LSM结合邻居干扰抵抗模型的传感器网络节点故障检测[J]. 湘潭大学自然科学学报, 2016, 38(1):101-105.

[10] 何明, 陈秋丽, 陈希亮,等. 鱼群启发的三维Ad hoc网络节点随机移动优化模型[J]. 仪器仪表学报, 2014，35(12):2826-2834.

[11] YOUNES O, THOMAS N. Analysis of the expected number of hops in mobile Ad Hoc networks with random waypoint mobility[J]. Electronic Notes in Theoretical Computer Science, 2011, 27(5):143-158.

责任编辑：龙顺潮

The Reliability Evaluation Scheme for MANET Based on Connection Matrix

ZHAOHe1*,GAILing2

(1.Department of Computer Science and Technology, Chengdu Neusoft University, Chengdu 611844;2.School of management,Shanghai University,Shanghai 200444 China)

The dynamic topology of mobile Hoc Ad network (MANET) makes it difficult to evaluate the reliability of the network, so a reliability evaluation scheme for MANET based on connection matrix is proposed. First, the source-terminal node pair and relay nodes in the network are determined. Then, the relay link state is detected according to the Euclidean distance between nodes and the communication range, so as to construct the connection matrix. Finally, the network connectivity is determined based on the connection matrix, and the average of connectivity value in some rounds is regard as the reliability of the network. In the simulation experiment, the influence of the node mobility model, the network size, the number of nodes and the range of communication on the network reliability is evaluated, which can provide a strong basis for network designers.

mobile Ad Hoc network; network reliability; connection matrix; node mobility model

2016-03-22

四川省教育厅科研项目(14ZB0350)

赵荷(1982-)，女,四川 荣县人，讲师.E-mail:zhaohe@nsu.edu.cn.

TP393

A

1000-5900(2016)03-0113-05