混凝土强度尺寸效应的本构描述及其数值实现*

赵 冰， 朱浩睿， 杨荣锋， 贺剑辉

(长沙理工大学 土木与建筑学院，湖南 长沙 410004)



混凝土强度尺寸效应的本构描述及其数值实现*

赵 冰*， 朱浩睿， 杨荣锋， 贺剑辉

(长沙理工大学 土木与建筑学院，湖南 长沙 410004)

大量试验表明混凝土强度存在尺寸效应.为了清晰表达出尺寸效应的物理本质，基于I阶梯度损伤理论给出了混凝土强度尺寸效应的本构描述；在有限单元网格的高斯点上建立非均匀的正交有限差分网格，构造相应数值算法.数值模拟结果表明：混凝土梁的名义抗弯强度Mnom随着梁深d的减小而单调减小，Mnom随内部特征长度的增大而单调增大，与文献中的实验结果相吻合，利用I阶梯度损伤理论解释混凝土强度尺寸效应现象是可行的.

混凝土；强度；尺寸效应；I阶梯度损伤；非均匀正交网格有限差分

大量试验表明，混凝土强度随着构件尺寸的增大而减小[1-3](即混凝土强度存在尺寸效应).目前大尺寸混凝土构件的设计仍然采用小尺寸构件的设计理论方法，这将影响混凝土结构的安全性与可靠性评估，给大尺寸混凝土结构带来安全隐患.

目前混凝土强度尺寸效应研究主要存在3种理论：①Weibull尺寸效应统计理论[4]；②Bažant尺寸效应律[5-7]；③裂纹的分形特性引起的尺寸效应理论[8-9].其中，Weibull理论认为混凝土强度尺寸效应是由材料强度的随机分布引起，结构强度取决于强度最弱的单元，但该理论没有考虑混凝土材料的微观结构，并且忽略了断裂过程中的应力重分布.Bažant尺寸效应律认为混凝土强度尺寸效应是由宏观裂纹扩展时应变能耗散引起.Carpinieri的多重分形尺寸效应理论认为，裂纹在不同观察尺度下的分形差异是材料产生尺寸效应的根源，该理论并非基于严格的力学推导，而是依赖于几何形象及部分直觉.

以上3种尺寸效应理论分别从不同的角度阐述了尺寸效应的产生原因，但都没能基于力学推导清晰表达出尺寸效应的物理本质，而是基于实验拟合的经验公式.

本文将在I阶梯度损伤理论的基础上，给出混凝土强度尺寸效应的本构描述，在有限元网格的高斯点上构造非均匀正交网格有限差分算法求解损伤梯度，编制程序来数值模拟混凝土悬臂梁抗弯强度的尺寸效应.

1 I阶梯度损伤理论与混凝土损伤演化率

1.1 I阶梯度损伤理论

为弥补经典连续介质理论及非局部损伤理论的缺陷，在[10]中，作者从热力学基本定律出发，将应变张量εij、标量损伤变量D、损伤变量的梯度D,m=∂D/∂xm(m=x,y,z)作为Helmholtz自由能函数Ψ的状态变量.

Ψ=Ψ(εij,D,D,m).

(1)

由于混凝土是一种由骨料、砂浆和它们之间的过渡区(粘结带)组成的三相非均质复合材料，因此，混凝土的损伤只能代表相当小而非无穷小体积(代表性体积)上的统计平均值[11].定义lm=∂D/∂D,m(m=x,y,z)为材料的内部特征长度参数.lm具有长度的量纲，反映材料微结构间相互作用的尺度.其物理含义为：损伤一旦发生，损伤梯度也将随之发生.lx,ly,lz分别为材料在x,y,z方向的内部特征长度参数.

对Helmholtz自由能函数Ψ(εij,D,D,m)在无初应力的自然状态附近作Taylor展开，在展开式中，保留到应变εij的二次项，保留到D的N阶项，保留到损伤梯度D,m的一次项.于是，Ψ可表达为

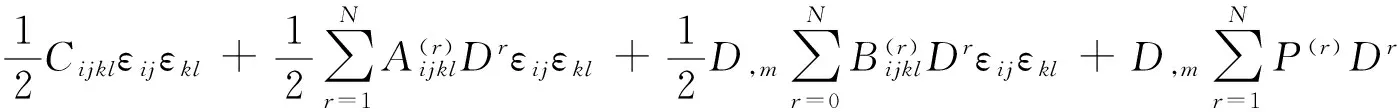
(2)

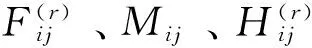
在任意损伤状态下将材料卸载至自然状态，考虑到此时εij=0，σij=0，且由于损伤不可逆，D≠0，D,m≠0，可得

(3)

将式(2)和式(3)代入σij=∂Ψ/∂εij，可得

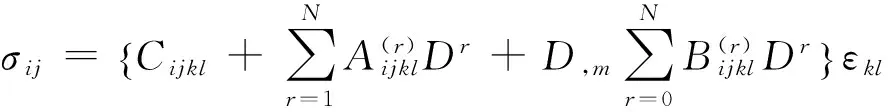
(4)

σij=Cijklεkl(1-D)(1+lmD,m).

(5)

1.2 混凝土损伤演化率

采用Häußler-Combe于2009年提出的混凝土损伤演化律[12]，该损伤演化律可以描述混凝土的损伤演化规律.在单向应力状态下时，通过引入等价应变κd，以相同形式描述拉应变和压应变：

(6)

其中，ε为轴向应变，αt为大于0的等价转换参数，κd为等价应变.

如图2所示，损伤演化律为

(7)

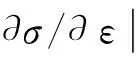
1.3 混凝土强度尺寸效应的物理机制

经典连续体理论认为：一点的应力仅仅是该点的应变及变形历史的函数，而与其周围点的场变量(如损伤)无关.而事实上，由于连续性假设不能严格满足，损伤等力学量代表的只是相当小而非无穷小体积上的统计平均值.在损伤梯度不大时，统计平均值可以恰当地描述介质的力学响应；出现较高的损伤梯度时，在相当小而非无穷小体积上的损伤将呈现高次非线性变化，经典损伤理论所代表的统计平均值就不能如实地反映出材料在相当小体积上的强度和变形行为.另外，由于经典连续体理论没有提供材料的内部长度参数，从量纲分析可知，即使是在不同的结构尺寸下，它必然也将得到与尺寸无关的解答，因而，无法预测材料破坏的尺寸效应.

预测材料破坏的尺寸效应时，需要对经典理论做出改进.有效的且具根本性的改进措施，是在经典连续理论的本构方程中引入梯度项及内部长度参数.损伤梯度项的出现暗示和反映了这样的事实：1)在某种尺度(细观和微观)下，混凝土微结构间的相互作用使得变形是非局部的；2)损伤梯度项及内部长度参数描述了混凝土的不均匀性，即描述了混凝土微结构之间的影响及作用.

I阶梯度损伤理论通过在混凝土的损伤本构方程中引入损伤梯度，进而利用损伤变量和损伤梯度的比值引入内部长度参数.由于内部长度参数的引入，不同尺寸下，混凝土的本构响应也必将不同，由此，I阶梯度损伤理论在强度尺寸效应的模拟上就具有了独特的优势.

2 混凝土尺寸效应的数值描述

2.1 损伤理论有限元实现的一般步骤

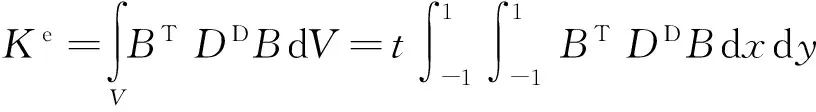
(8)

其中，DD为弹性损伤矩阵.对于平面应变问题，弹性损伤矩阵DD有如下形式：

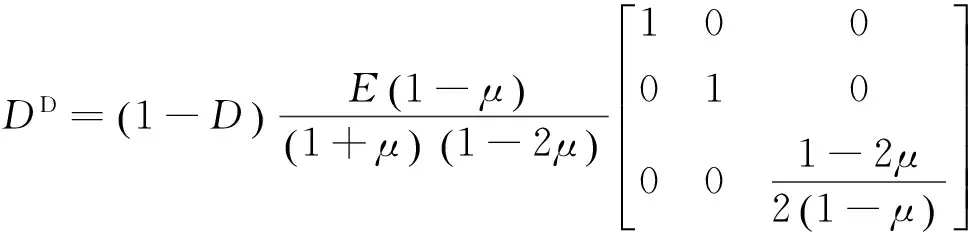
(9)

其中，E为弹性模量，μ为泊松比.损伤变量D可由损伤演化律式(7)得到.由此，经典损伤理论的有限元方程将表达为式(10)的非线性方程组：

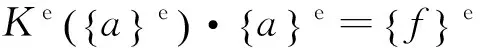
(10)

通过单元组装和迭代算法，即可求出结构在不同荷载下的变形、应变、损伤和应力.

2.2 非均匀网格有限差分法

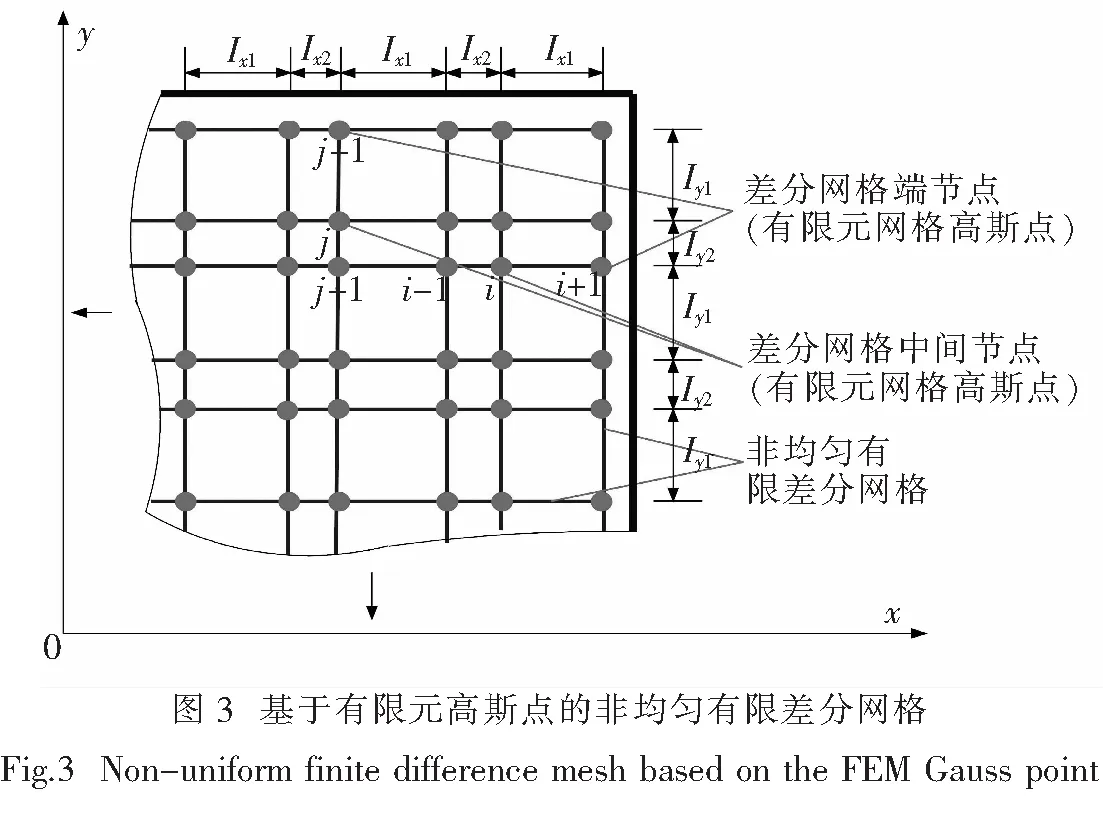
I阶梯度损伤理论的本构方程中，模型不但包含了损伤，还包含了损伤梯度.为了计算式(5)中的损伤梯度D,m，需要构造损伤梯度的数值算法.如图3所示，利用有限单元网格的高斯点构成非均匀的正交有限差分网格.正交差分网格中，x、y方向分别具有两种不同的网格间距：Ix1、Ix2和Iy1、Iy2.当高斯点的损伤已知时，损伤梯度可由非均匀有限差分算法得到.

在邻近节点i处，损伤变量可以展开为泰勒级数：

(11)

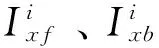
(12)

类似地，在y方向可得：

(13)

(12) 式 、(13)式即为差分网格的中间节点损伤梯度的二阶有限差分格式.

同理，由差分网格端节点的损伤梯度的二阶有限差分格式可得：

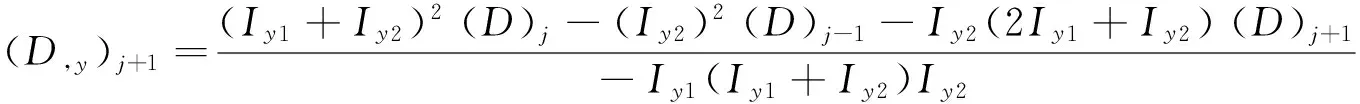
(14)

(15)

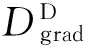
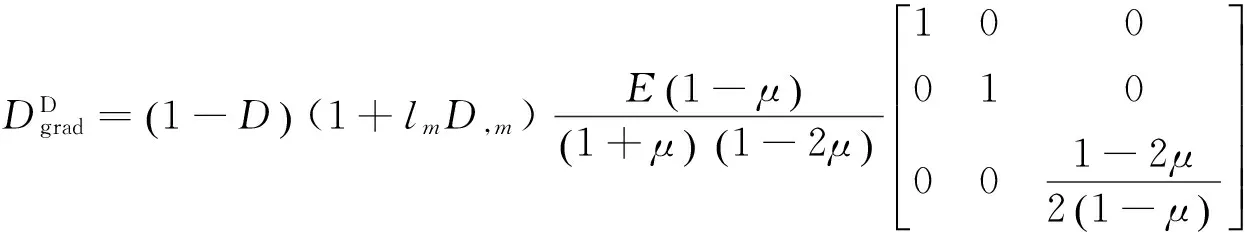
(16)

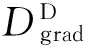
3 数值模拟及结果分析

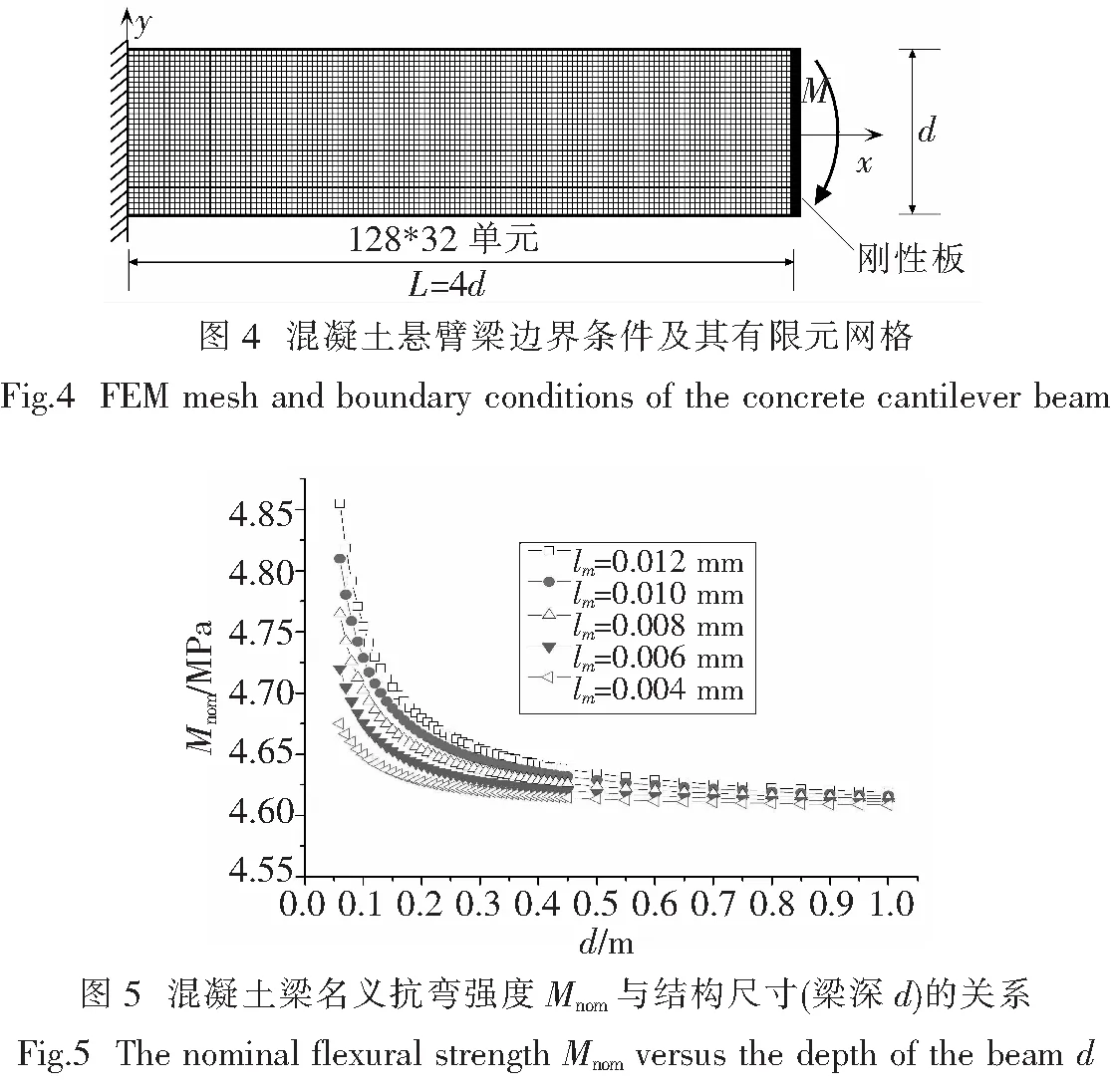
如图4所示,长度L与深度d之比为4的悬臂梁，粱厚为b，左侧为悬臂端，右侧设置刚性板以保证平截面假设成立.在刚性板上施加一个力偶M.采用8节点平面应变单元模拟，有限单元网格由12 609个节点和4 096个单元组成.定义最大正应变达到εct时的弯矩Mf为极限弯矩，归一化的名义抗弯强度Mnom=6Mf/d2b.

利用前述编制的I阶梯度损伤有限元程序计算不同梁深下混凝土的名义抗弯强度Mnom.名义抗弯强度Mnom同梁深d的关系如图5所示.可以看出，Mnom随着梁深d的减小而单调减小，Mnom随内部特征长度的增大而单调增大.该模拟结果和[13]的实验结果相吻合.拟合图5的曲线，可得：

(17)

式(17)即为混凝土无刻痕纯弯梁抗弯强度尺寸律.A、b1为拟合参数.

4 结 论

(1) 由于I阶梯度损伤理论在本构方程中引入了损伤梯度及内部长度参数，利用I阶梯度损伤理论解释混凝土强度尺寸效应现象是可行的.

(2) 对于正交有限元网格，可利用有限单元网格的高斯点构成非均匀的正交有限差分网格求解损伤梯度.

(3) 数值模拟结果表明：混凝土梁的名义抗弯强度Mnom随着梁深d的减小而单调减小，Mnom随内部特征长度的增大而单调增大.

[1] SABNIS G M,MIRZA S M. Size effect in model concretes[J]. American Society of Civil Engineers, 2014(105): 1007-1020.

[2] NEVILLE A M. The influence of size of concrete test cubes on mean strength and standard deviation[J]. Magazine of Concrete Researeh,1956(8): 101-110.

[3] 冷发光, 邢锋, 冯乃谦,等. 粉煤灰高性能混凝土试件强度尺寸效应研究[J]. 混凝土, 2000(12): 18-19.

[4] WEIBULL W A. A statistical distribution function of wide applicability[J]. Applied Mechanics, 1951, 18(2): 233-234.

[5] BAŽANT Z P. Probability distribution of energetic-statistical size effect in quasibrittle fracture[J]. Probabilistic Engineering Mechanics, 2004, 19(4): 307-319.

[7] BAŽANT Z P. Size effect in blunt fracture: concrete, rock, metal[J]. American Society of Civil Engineers, 2014, 110(4): 518-535.

[8] CARPINTERI A,CHIAIA B,CORNETTI P, et al. Comments on “Is the cause of size effect on structural strength fractal or energetic-statistical?” by Bažant & Yavari [Engng Fract Mech,2005,72:1-31][J]. Engineering Fracture Mechanics, 2007, 74(17): 2892-2896.

[9] CARPINTERI A. Scaling laws and renormalization groups for strength and toughness of disordered materials[J]. International Journal of Solids and Structures, 1994(31): 291-302.

[10] ZHAO B,ZHENG Y R,ZENG M H, et al. First-order gradient damage theory[J]. Applied Mathematics and Mechanics, 2010, 31(8): 987-994.

[11] 赵冰, 李宁, 盛国刚. 软化岩土介质的应变局部化研究进展——意义·现状·应变梯度[J]. 岩土力学, 2005(03): 494-499.

[12] HäUßLER-COMBE U, KITZIG M. Modeling of concrete behavior under high strain rates with inertially retarded damage[J]. International Journal of Impact Engineering, 2009, 36(9):1106-1115.

[13] BAŽANT Z P,CHEN E P. Scaling of structure failure[J].American Society of Mechanical Engineers, 1997, 50(10): 593-627.

责任编辑：罗 联

The Constitutive Description of Size Effect on Strength of Concrete and Its Numerical Implementation

ZHAOBing*,ZHUHao-rui,YANGRong-feng,HEJian-hui

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410004 China)

The size effect on strength of concrete is obtained from many experiments. Based on the first-order gradient damage theory, the constitutive description of the size effect of concrete strength is given. The constitutive can express the physical essence of size effect. A non-uniform orthogonal finite difference mesh based on the Gauss point of the finite element mesh is established. The corresponding numerical algorithm of the first-order gradient damage theory is constructed. The simulation results show that the nominal flexural strength Mnomdecreases monotonously with the decrease of the deep beamd, and increases monotonously with the increase of the internal characteristic length. The numerical results match to the experimental results. The size effect on strength of concrete can be explained by the first-order gradient damage theory.

concrete；strength; size effect; first-order gradient damage theory; non-uniform orthogonal finite difference mesh

2016-02-10

土木工程湖南省优势特色重点学科创新性项目(13ZDXK12)

赵冰(1972-)，男，湖南 涟源人，博士,副教授. E-mail:zhaob_m-y@163.com

TU375

A

1000-5900(2016)03-0035-06