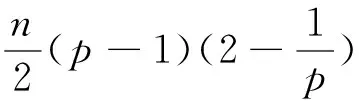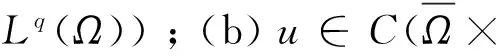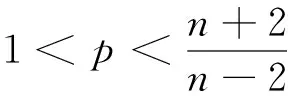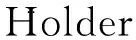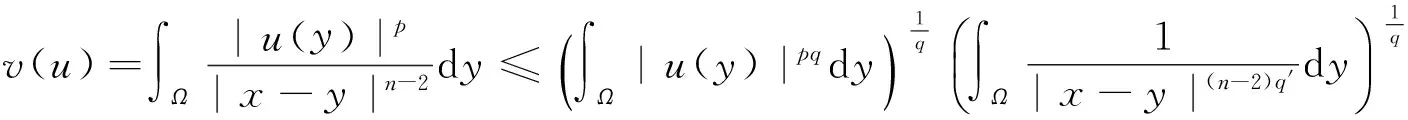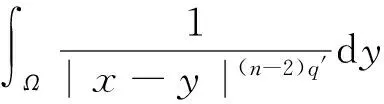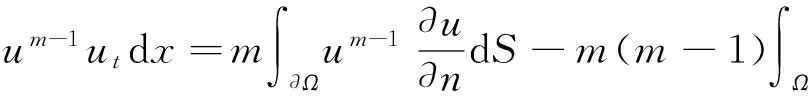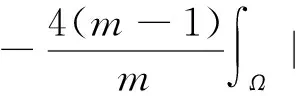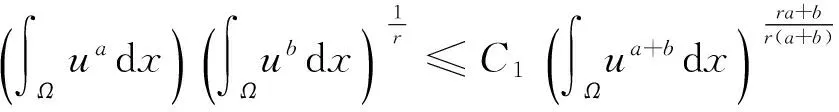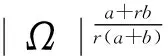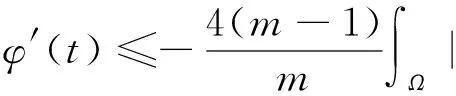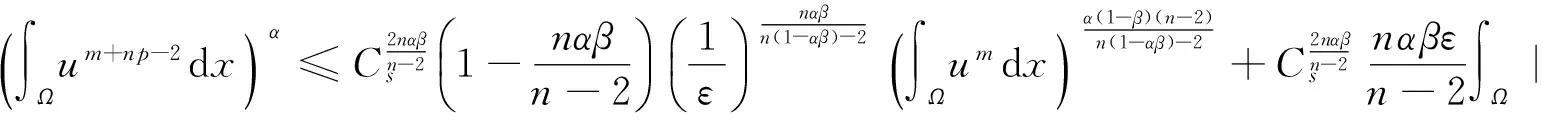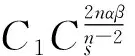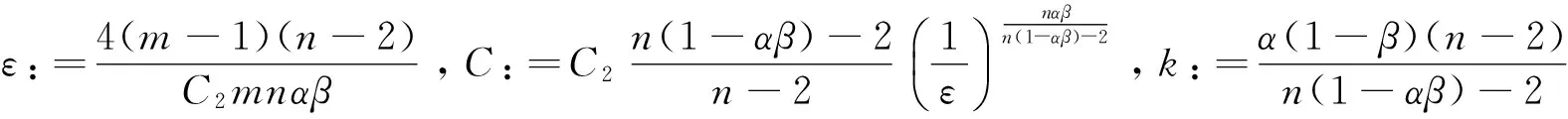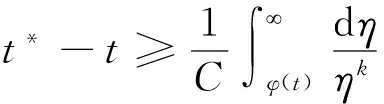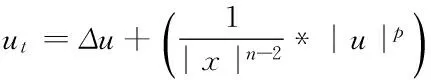一类带非局部项的抛物型方程爆破时间的下界问题*

2016-02-07王忠谦宋明亮

湘潭大学自然科学学报 2016年3期

关键词：下界南京师范大学抛物

王忠谦，宋明亮,2*

(1.江苏第二师范学院数学与信息技术学院，江苏南京 210013；2.南京师范大学数学科学学院，江苏南京 210046)

一类带非局部项的抛物型方程爆破时间的下界问题*

王忠谦1，宋明亮1,2*

(1.江苏第二师范学院数学与信息技术学院，江苏南京 210013；2.南京师范大学数学科学学院，江苏南京 210046)

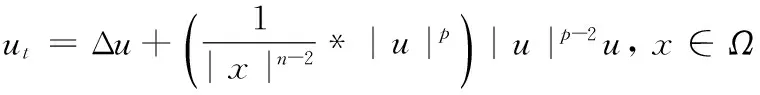
爆破时间；Dirichlet边界条件；Sobolev不等式

在[1]中，Payne和Schaefer得到了半线性抛物方程ut=Δu+f(u)在齐次Dirichlet边界条件下解的爆破时间的下界，这里，f满足某些适当的假设.从那以后，带Dirichlet边界条件的各类抛物方程解的爆破时间的下界被广泛研究(见[2-6]及其参考文献).在[7]中，作者研究了问题

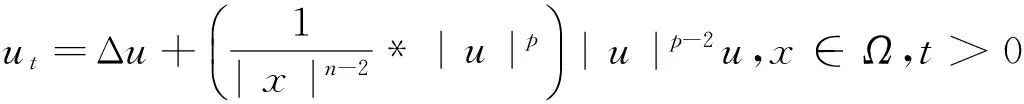
(1)

u(x,t)=0,x∈∂Ω,t>0,

(2)

u(x,0)=u0(x),x∈Ω,

(3)

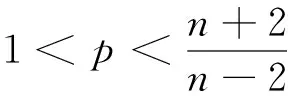
受到以上工作的启发，本文中对于问题(1)～(3)，在1

我们有如下主要结论：

为证明定理1，需要先证明如下引理.

‖v(u)‖.特别地，‖v(u)‖.

‖v(u)‖.

(4)

特别地，当q=n-1时，(4)可写作‖v(u)‖≤C(Ω ,n).

下面我们估计爆破时间t*的下界和爆破率的下界.

定理1的证明：设φ(t):=∫Ωumdx，则利用分部积分公式和引理2,

(5)

(6)

再由Sobolev不等式(见[12])

(7)

(8)

(9)

(10)

由于Y(φ)关于φ单调递减，故Y存在反函数Y-1且Y-1仍为单调递减函数.由(10)可得爆破率的下估计，φ(t)≥Y-1(t*-t).

[1] PAYNE L E,SCHAEFER P W. Lower bounds for blow-up time in parabolic problems under Dirichlet conditions[J]. J Math Anal Appl,2007,328:1196-1205 .

[2] PAYNE L E,PHILIPPIN G A,SCHAEFER P W. Blow-up phenomena for some nonlinear parabolic problems[J]. Nonlinear Anal,2008,69:3495-3502.

[3] PAYNE L E, SONG J C. Lower bounds for blow-up time in a nonlinear parabolic problem [J]. J Math Anal Appl,2009,354:394-396.

[4] SONG J C. Lower bounds for the blow-up time in a non-local reaction-diffusion problem[J]. Applied Mathematics Letter,2011,24:793-796.

[5] LIU D M,MU C L,QIAO X. Lower bounds estimate for the blow-up time of a nonlinear nonlocal porous medium equation[J]. Acta Math Sci Ser B Engl Ed,2012,32:1206-1212.

[6] BAGHAEI K, MOHAMMAD B G, MAHMOUD H. Lower bounds for the blow-up time in a semilinear parabolic problem involving a variable source[J]. Applied Mathematics Letter,2014,27:49-52.

[7] LIU B,MA L. Invariant sets and the blow up threshold for a nonlocal equation of parabolic type[J]. Nonlinear Anal,2014,110:141-156.

[8] LACEY A A. Thermal runaway in a non-local problem modelling Ohmic beating: Part 1: Model derivation and some special cases[J].European J Appl Math 1995,6(2):127-144.

[9] GOURLEY S A. Travelling front solutions of a nonlocal Fisher equation[J]. J Math Biol,2000,41(3):272-284.

[10] OU C,WU J. Persistence of wavefronts in delayed nonlocal reaction-diffusion equations[J]. J Differential Equations,2007,235(1):219-261.

[11] SO J W H,WU J,ZOU X. A reaction-diffusion model for asingle species with age structure.I Travelling wavefronts on unbounded domains[J]. Proc Lond Math Soc A,2012,457:1841-1853.

[12] TALENTI G. Best constant in Sobolev inequality [J].Ann Mat Pura Appl,1976,110:353-372.

责任编辑：龙顺潮

Lower Bound for a Nonlocal Equation of Parabolic Type

WANGZhong-qian1,SONGMing-liang1,2*

(1. Mathematics and Information Technology School, Jiangsu Second Normal University, Nanjing 210013；2. School of Mathematical Sciences,Nanjing Normal University, Nanjing 210046 China)