特性关系下概率粗糙集中的属性核计算方法*

刘 芳， 牟廉明,2*

(1.内江师范学院 数学与信息科学学院，四川 内江 641100；2.数据恢复四川省重点实验室，四川 内江 641100)



特性关系下概率粗糙集中的属性核计算方法*

刘 芳1， 牟廉明1,2*

(1.内江师范学院 数学与信息科学学院，四川 内江 641100；2.数据恢复四川省重点实验室，四川 内江 641100)

提出了在特性关系下的概率粗糙集模型中的概率近似精度的增量更新机制，通过比较概率近似精度的更新值得到属性核，最后提出了一种在特性关系下概率粗糙集模型中的属性核求解算法，并举例说明了所提算法的有效性和可行性．

概率粗糙集；特性关系；边界集；更新近似集

粗糙集理论是一种有效处理模糊、不确定问题的数学工具，已被应用到许多研究领域，如机器学习、数据挖掘、知识发现和智能数据分析等[1-2]．属性约简是粗糙集理论中最重要的研究内容之一，通过属性约简可以提高分类学习算法的性能、简化数据描述和避免过拟合[3-4].属性核的计算对解决这一问题具有极其重要的意义，因为属性核中的所有属性在系统的任何约简结果中都是必须的.将约简结果初始化为属性核，可以有效地减少约简算法在属性空间中的搜索范围，极大地缩短算法的运行时间.如何高效地计算一个给定的决策系统的属性核极其关键，它可以极大地影响算法的总体效率．文献对如何得到属性核的讨论很少，相应的属性约简算法或者不提及计算属性核的方法，或者只是简单地指明直接引用Hu的研究结果[5]．

经典粗糙集模型假设的分类必须是完全正确或确定的，因此，它不能有效地处理有噪声的数据和挖掘其潜在的有用知识．为了解决这种问题，众多研究学者通过引入概率阈值提出了很多扩展概率粗糙集模型，如0.5概率粗糙集模型、变精度粗糙集模型和决策粗糙集模型等[6,13]．由于在概率粗糙集模型中属性集的变化对分类区域的影响不再具有单调性，所以经典粗糙集中的属性约简方法在概率粗糙集模型中不再适用.众多研究学者对这一问题展开了深入研究．Chen等基于容差矩阵和属性核的最小约简的概念，提出了变精度粗糙集的属性核思想，并给出了基于属性核的启发式约简以求解最小约简[6]；Jia等以决策成本最小化为目标函数，分别提出了启发式算法、遗传算法和模拟退火算法来对决策粗糙集模型中的属性约简问题进行优化[7]；Jia等还设计了一种自适应学习算法来得到决策粗糙集中的成本函数和阈值，并提出了一种用粒子群优化方法来计算属性约简的方法[8]；Wang等给出了在概率粗糙集中进行启发式属性约简时的单调不确定性度量方法[9]，具有较高性能．然而，当单个属性删除时该方法需要频繁地计算概率近似精度的更新值来得到属性核．这种重复性的计算导致算法的时间复杂度和空间复杂度都较高，而且导致错误率增加，最终使得算法的效率低下．

增量学习方法是一种在当前的样本训练中充分利用了历史的训练结果，从而显著地减少了后续训练时间的技术，可大幅提高分类的效率．开发基于增量学习技术的高效知识获取方法，已成为粗糙集理论与方法研究中的一个热点问题．例如，Chan提出了Pawlak粗糙集模型中边界集的定义，并利用边界集的更新计算实现了Pawlak粗糙近似集的增量式计算方法[10]；Li提出了在特征关系粗糙集模型下利用边界集增量式计算近似集的方法[11]；Chen提出了一种当属性值粗化和细化时近似集的增量更新方法[12]；Luo提出了在集值有序决策信息系统中当属性泛化时近似集的动态更新方法[14]；Zhang提出了复合粗糙集模型中当对象发生变化时近似集的增量式更新方法[15]．本文针对[9]中对概率粗糙集模型中属性核的计算方法进行了改进，分析了在特性关系下概率粗糙集模型中的概率近似精度的增量式计算方法，进一步给出了概率粗糙集模型中基于边界集的属性核的一种快速求解算法．最后，通过实例分析进一步验证本文所提方法的有效性和可行性．

1 定 义

本节简要介绍特性关系的基本概念[11,17]、概率粗糙集模型的基本概念及其属性核计算方法[9,16]．

1.1 特性关系概念

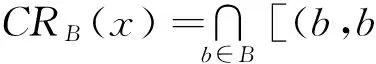
1.2 概率粗糙集模型

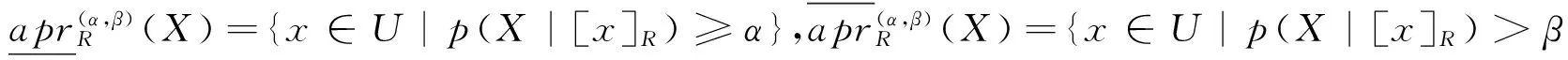
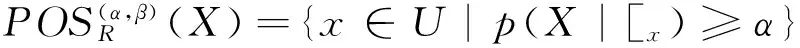
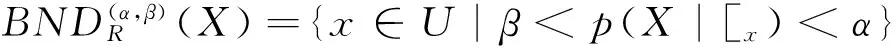
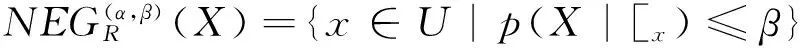
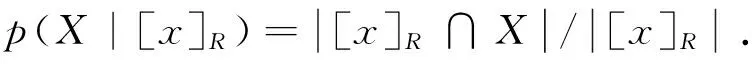
定义2[9]给定决策信息系统DS=(U,C∪D)，0≤β<α≤1，C为条件属性集，D为决策属性集，R⊆C，U/D={Y1,Y2,…,YM}为U中划分的决策类集合，D关于C的概率上、下近似集分别定义为：

[9]同时定义了概率近似精度为：对于j∈{1,2,…,M}，

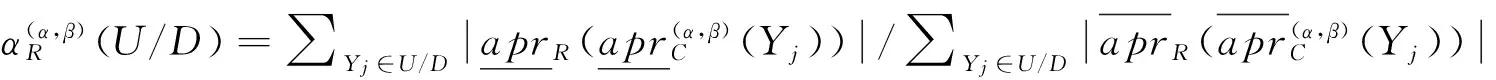
定义3[9]给定一个决策信息系统DS=(U,C∪D)，0≤β<α≤1，R⊆C，R是DS在概率粗糙集模型下的属性约简，当且仅当下列式子成立：

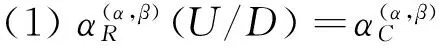
因此，[9]定义了概率粗糙集模型下的属性核为：

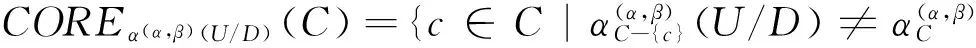
2 特性关系下属性核计算方法

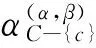
2.1 理论分析

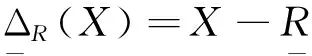
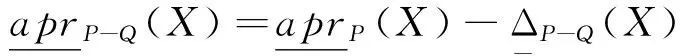
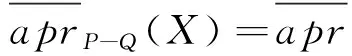
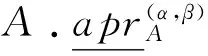
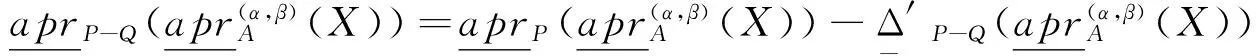
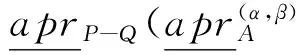
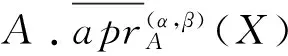
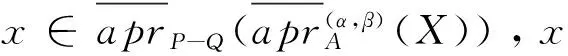
根据引理1和引理2和定义7可以得到定理3．

定理3 给定一个决策信息系统DS=(U,C∪D)，0≤β<α≤1，Q⊂R⊆C，U/D={Y1,Y2,…,YM}为U中划分的决策类集合，当从属性集R中删除属性集Q时，特性关系下的概率粗糙集中的概率近似精度更新如下：

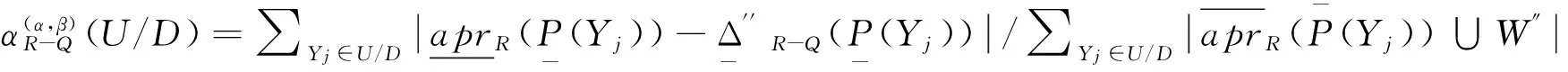
证明 根据定义7可知

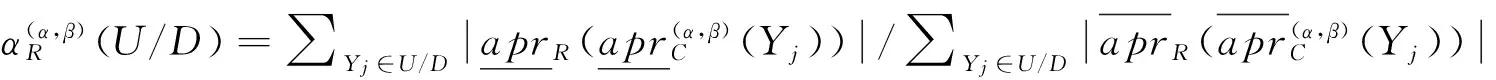
由引理1～2、定理3可知特性关系下的概率粗糙集模型中概率近似精度的求解可通过边界集的计算实现增量式的更新求解，进而避免重复的计算．基于此，本文给出了特性关系下的概率粗糙集模型中属性核的增量式求解算法．

2.2 算法描述

算法1：特性关系下概率粗糙集的属性核计算．

输入：一个决策表DS=(U,C∪D)，阈值(α,β)，U={x1,x2,…，xK} ，C={a1,a2,…,an}，U/D={Y1,Y2,…,YM}．

输出：特性关系下概率粗糙集的属性核COREα(α,β)(U/D)(C)．

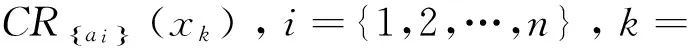
Step 2 计算CRC(xk).

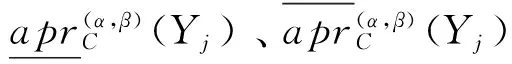
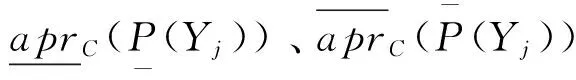
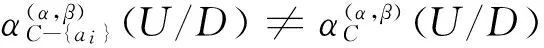
Step 7 COREα(α,β)(U/D)(C)就是要得到的特性关系下概率粗糙集模型的属性核．

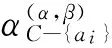
表1 一个决策信息系统Tab.1 A decision table

3 算 例

给定决策信息系统DS=(U,C∪D)如表1所示，U={x1,x2,…,x8}，C={a1,a2,a3,a4,a5}，D={d}．设α=0.75，β=0.55.根据表1计算特性关系下单个属性特性集、所有条件属性集下的特性集和决策属性分类集合为：

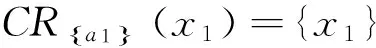
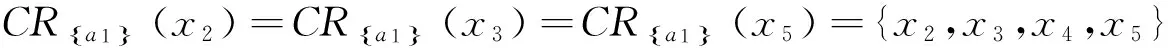
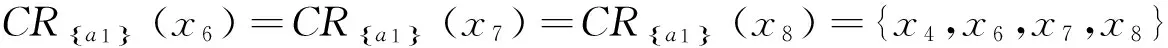
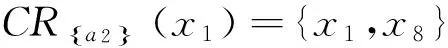
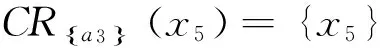
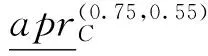
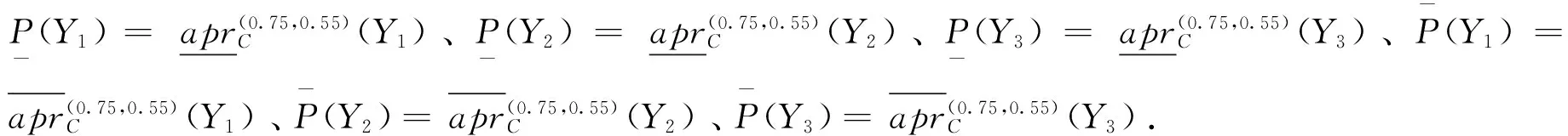
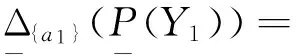
4 结束语

本文用增量学习方法提出了特性关系下的一种基于概率粗糙集的属性核计算方法，用特性关系粗糙集中增量式更新上、下近似集的方法来计算概率粗糙集中当单个属性减少时的上、下近似集．进一步得到概率近似精度，通过比较概率近似精度的值是否相等得到属性核.理论分析和实例表明，本文提出的特性关系下概率粗糙集中基于边界集的属性核计算方法是可行的．

[1] HERAWAN T, DERIS M M,ABAWAJY J H. A rough set approach for selecting clustering attribute[J], Knowledge-Based Systems, 2010, 23(3):220-231.

[2] LIN T Y,SYAU Y R. Unifying variable precision and classical rough sets: granular approach[C]//Rough Sets and Intelligent Systems-Professor Zdzisaw Pawlak in Memoriam, Springer, 2013,43: 365-373.

[3] PARTHALAIN N M,SHEN Q,JENSEN R. A distance measure approach to exploring the rough set boundary region for attribute reduction[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(3): 305-317.

[4] THANGAVELA K, PETHALAKSHMI A. Dimensionality reduction based on rough set theory: A review[J]. Applied Soft Computing, 2009, 9(1): 1-12.

[5] HU X H, CERCONE N. Learning in relational databases:a rough set approach[J]. Computational Intelligence, 1995,11(2):323-337.

[6] CHEN H,YANG J A,ZHUANG Z Q. The core of attributes and minimal attributes reduction in variable precision rough set[J]. Chinese Journal of Computers, 2012, 35(5):1011-1017.

[7] JIA X Y,LIAO W H,TANG Z M,et al. Minimum cost attribute reduction in decision-theoretic rough set models[J]. Information Sciences, 2013, 219(10): 151-167.

[8] JIA X Y,TANG Z M, LIAO W H,et al. On an optimization representation of decision-theoretic rough set model[J]. International Journal of Approximate Reasoning, 2014, 55(1): 156-166.

[9] WANG G Y,MA X A,YU H. Monotonic uncertainty measures for attribute reduction inprobabilistic rough set model[J]. International Journal of Approximate Reasoning, 2015, 59: 41-67.

[10] CHAN C C. A rough set approach to attribute generalization in data mining[J]. Journal of Information Sciences, 1998, 107: 169-176.

[11] LI T R. A rough sets based characteristic relation approach for dynamic attribute generalization in data mining[J]. Knowledge-Based Systems, 2007, 20: 485-494.

[12] CHEN H M,LI T R,QIAO S J,et al. A rough set based dynamic maintenance approach for approximations in coarsening and refining attribute values[J]. International Journal of Intelligent Systems, 2010, 25(10):1005-1026.

[13] LIU D, LI T R,RUAN D,et al. An incremental approach for inducing knowledge from dynamic information systems[J]. Fundamenta Informaticae, 2009, 94(2): 245-260.

[14] LUO C,LI T R,ZHANG J B. Dynamic maintenance of approximations in set-valued ordered decision systems under the attribute generalization[J]. Information Sciences, 2014, 257(2): 210-228.

[15] ZHANG J B,LI T R,CHEN H M. Composite rough sets for dynamic data mining[J]. Information Sciences, 2014, 257: 81-100.

[16] YAO Y Y. Two semantic issues in a probabilistic rough set model[J]. Fundamenta Informaticae, 2011, 108(3): 249-265.

[17] GRZYMALA-BUSSE J W.Characteristic relations for incomplete data:a generalization of the indiscernibility relation[J]. Transactions on Rough Sets,2005(IV):58-68.

责任编辑：龙顺潮

Calculation Method for Attribute Core of Characteristic Relation in Probabilistic Rough Sets

LIUFang1，MOULian-ming1,2*

(1.College of Mathematics and Information Science, Neijiang Normal University, Neijiang 641100；2.Data Recovery Key Laboratory of Sichuan Province, Neijiang 641100 China)

In this paper, incremental approaches for computing the probabilistic approximation accuracy in probabilistic rough sets under the characteristic relation are presented. The attribute core is obtained by comparing the updated values of the probabilistic approximation accuracy. Finally, the algorithm for calculating the attribute core based on probabilistic rough sets under the characteristic relation is developed. And the effectiveness and feasibility of the proposed algorithm for attribute core are validated by illustrative examples.

probabilistic rough sets; characteristic relation; boundary sets; updating approximations

2016-03-05

四川省教育厅自然科学重点项目基金(13ZA0008)；内江师范学院自然科学重点项目基金(12NJZ03)；内江师范学院专利科研项目(15ZL02)；2015年内江市科技支撑计划项目

牟廉明(1971-)，男，重庆 万州人，教授.E-mail:lytb@163.com

O242

A

1000-5900(2016)03-0001-07