EEMD能量熵与优化LS-SVM的滚动轴承故障诊断*

陈法法，李 冕 ，陈保家，陈从平

(三峡大学 a.新能源微电网湖北省协同创新中心；b.水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002)

EEMD能量熵与优化LS-SVM的滚动轴承故障诊断*

陈法法a,b，李 冕b，陈保家b，陈从平b

(三峡大学 a.新能源微电网湖北省协同创新中心；b.水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002)

针对滚动轴承振动故障信号非平稳、非线性难以有效诊断的问题，提出基于集成经验模式分解(ensemble empirical mode decomposition，EEMD)能量熵与优化最小二乘支持向量机(least square support vector machine，LS-SVM)的滚动轴承故障诊断方法。首先利用EEMD对滚动轴承的振动故障信号进行分解，得到各阶的内禀模态函数分量(IMF)并计算其能量构造成特征向量矩阵，随后将该特征向量矩阵输入给优化的LS-SVM进行故障模式的分类辨识。通过实验验证了该方法的有效性和可行性，结果表明，基于EEMD能量熵特征与优化LS-SVM的滚动轴承故障诊断方法能够有效的诊断滚动轴承的实际运行工况。

集成经验模式分解; 最小二乘支持向量机; 滚动轴承; 故障诊断

0 引言

滚动轴承出现异常故障时的振动信号多表现为非平稳、非线性特性[1-2]，集成经验模式分解(ensemble empirical mode decomposition，EEMD)作为一种基于数据驱动的时频信号分析方法，通过在原始信号中添加高斯白噪声，有效抑制了分解中的模式混叠问题。当滚动轴承发生不同故障时，振动信号的特征频率以及频率范围内的幅值能量都将发生变化，为此可对滚动轴承的振动故障信号进行EEMD分解，得到各阶的内禀模态分量(IMF)再计算其能量作为滚动轴承的故障特征[3-4]。

支持向量机(support vector machine，SVM)作为一种智能化的故障诊断模型，基于结构风险最小化原则，有效避免了过学习、欠学习及维数灾难问题，同时对于故障样本稀缺的小子样故障诊断问题也表现出优良特性[5]。最小二乘支持向量机(least square support vector machine，LS-SVM)在传统SVM的基础上进一步优化，降低了SVM的计算复杂度，提高了运算效率[6-7]。

为此，本文提出基于EEMD能量熵与优化LS-SVM的滚动轴承故障诊断方法，首先利用EEMD对滚动轴承的故障振动信号进行分解，EEMD能够有效获得滚动轴承振动信号的特征分布类型，构造出滚动轴承故障诊断的特征向量矩阵。随后将该特征向量矩阵输入给优化的LS-SVM进行故障模式的分类辨识，LS-SVM作为一种先进的智能诊断模型，能够快速实现滚动轴承故障的自动化、高精度的智能诊断。实验结果表明，该方法较之传统的故障诊断方法，效果更优，精度更高。

1 集成经验模式分解原理(EEMD)

1.1 集成经验模式分解(EEMD)

集成经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)是在EMD基础上，通过在测试信号中加入高斯白噪声，利用高斯白噪声的频率均匀分布特性，有效抑制EMD分解过程中的模态混叠，通过EEMD分解得到的 IMF分量更能客观真实的反映原始信号的物理内涵。

EEMD算法的实现过程如下：

(1)

(2)

(3)

EEMD分解保留了EMD的优点。在EEMD分解过程中，有两个重要参数需要设置，即：所加白噪声的幅值系数k和执行EMD分解的次数M。目前噪声的幅值系数k和执行EMD分解的次数M均没有确定的理论公式参考，在这里根据实践经验并多次尝试比较，设定白噪声的幅值系数k=0.2，执行EMD分解的次数M=100。

1.2 EEMD能量熵

信息熵是对系统不确定性程度的描述，当系统中的不确定性信息越多，则对应的熵值越大。当滚动轴承出现不同故障时，其振动信号的频率成分以及各频率段内信号的幅值能量均会发生改变。通过对振动信号进行EEMD分解，获取各个IMF的能量分布特征，结合信息熵理论，构造EEMD能量熵。

滚动轴承的振动故障信号经过EEMD分解将得到n个IMF分量，即：

(4)

分别计算各阶IMF分量的幅值能量E1,E2,…,En，即:

(5)

(6)

为了避免部分幅值能量集中的IMF分量控制了部分能量相对微弱的IMF分量，对各阶IMF分量的幅值能量进行归一化处理，即：

(7)

由此，相应的EEMD能量熵(entropy，EN)可表示为：

(8)

式中，pj是第j个IMF的幅值分量在总能量中所占的比重。

2 最小二乘支持向量机(LS-SVM)

(9)

图1 支持向量机的分类示意图

(10)

位于两类分类超平面中间的分类面则是最优分类超平面，支持向量机的目标则是最大化两类分类超平面之间的距离，此时优化模型转换为如下的二次规划问题：

(11)

(12)

最小二乘支持向量机(Least Square Support Vector Machine, LS-SVM)改变了标准支持向量机的求解形式，将式(12)中的不等式约束改为了等式约束，这样优化模型转换为如下的二次规划问题：

(13)

(14)

(15)

3 基于集成经验模式分解与LS-SVM的故障诊断模型

故障特征的有效提取以及故障特征的准确辨识是滚动轴承故障诊断的两个关键步骤，将EEMD应用于滚动轴承振动信号的故障特征提取，以EEMD分解得到的内禀模态分量计算其能量作为特征向量，随后将得到的特征向量输入给LS-SVM进行故障的分类辨识，整个故障诊断的流程如图2所示。在利用LS-SVM进行故障诊断时，参数的优化选择对故障诊断精度的影响很大，为此采用粒子群算法( particle swarm optimization, PSO)[8-9]对LS-SVM的惩罚参数值γ和核函数参数值α进行优化选择。

图2 基于EEMD与LS-SVM的故障诊断流程

当滚动轴承出现不同故障时，振动故障信号经EEMD分解后各个IMF分量中的能量会发生变化，因此，通过提取IMF的幅值能量作为滚动轴承的故障特征信息，具体步骤如下[11]：

(1)对滚动轴承的振动故障信号x(t)进行EEMD分解，提取分解后前n个IMF分量。C={c1,c2,…cn}各个IMF分量{c1,c2,…cn}包含着不同的频率成分，从而可以形成滚动轴承振动故障信号在不同频率域的能量分布。

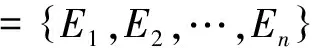
(16)

(17)

T′即为滚动轴承故障诊断过程中输入给LS-SVM的故障特征向量。

4 实例分析

4.1 实验设置

通过在滚动轴承故障实验台上模拟滚动轴承的不同故障状态验证本文所提方法的有效性，整个测试装置及传感器的布置如图3所示。实验系统包括驱动电机、单级齿轮箱、滚动轴承、制动器及其它附属部件组成。实验对象为安装在齿轮箱上面的支撑轴承，轴承故障均设置在电机输入轴的第一个端部轴承上，轴承型号为6206-2RS，轴承故障采用电火花加工的方法，分别在轴承的内圈、外圈人为制造损伤模拟滚动轴承的故障类型。

图3 滚动轴承测试装置示意图

电机驱动转轴带动齿轮旋转，转速为710 r/min，ICP加速度传感器安装在轴承座和齿轮箱的箱盖上，实验数据由奥地利的DEWETRON多功能振动信号采集仪获取，采样频率为10kHz。分别设置滚动轴承内圈损伤、外圈损伤和轴承内圈和外圈同时损伤三种故障状态，滚动轴承在不同状态下的时域波形如图4所示。注：轴承振动信号数据均在加载模式下采集，齿轮箱输出轴的端部载荷设置为17.5N·m。

图4 滚动轴承在不同状态下的时域波形图

4.2 故障诊断及结果分析

由图4可以看出滚动轴承在不同状态下的振动信号有一定的区别，但据此难以判断滚动轴承的具体故障。通过对信号进行简单的时域分析，计算出轴承振动信号在不同状态下的方根幅值Xr：

(18)

轴承在4状态下各取40个状态样本，由此共构造了160个状态样本，计算轴承振动信号在不同状态下的方根幅值如图5所示。

图5 轴承在不同状态下的方根幅值序列图

图5中，样本点数1～40为轴承正常状态，40～80为轴承内圈故障，80～120为轴承外圈故障，120～160为轴承混合故障。从图5可以看出，轴承的方根幅值在轴承故障状态时均大于其正常状态下的标准值，通过方根幅值指标可以判定轴承确实存在故障，但是，仅通过这个指标无法区分轴承究竟是何种故障，在图5中，轴承的方根幅值在轴承内圈故障、外圈故障、混合故障下很接近，难以区分。由此，简单的时域分析难以区分轴承的不同故障状态。

下面对轴承的故障信号进行EEMD分解，得到分解后的IMF，经过分析得知滚动轴承的故障信号存在于高频段，同时对分解后的各个IMF分量与原始振动信号进行相关分析，发现EEMD分解后的前8阶IMF已经涵盖了原始信号的几乎所有信息，因此这里只取振动信号的前8个IMF分量，图6是滚动轴承混合故障时振动信号经过EEMD分解后前8阶的IMF分布图。为了验证EEMD分解对轴承故障特征的敏感性，根据轴承振动信号在不同状态下的分解结果，分别计算滚动轴承在不同状态下的EEMD能量熵的平均值，计算结果如表1所示。

图6 滚动轴承混合故障时的EEMD分解图

轴承状态正常内圈损伤外圈损伤混合故障熵值0．53520．49830．38770．5111

由表1可以看出，轴承在不同状态下的EEMD能量熵值不同。由于轴承在正常状态下时，各个时间尺度的IMF分量相对比较平均，因此，轴承在正常状态下的EEMD能量熵值最大。当轴承内圈或外圈出现损伤时，在相应的故障频段内会出现能量聚集，因此，对应的EEMD能量熵值变小。当轴承出现混合故障时，在轴承内圈、外圈等故障频率段内均会出现能量聚集，因此，对应的EEMD能量熵值又有一定增大。由此可以看出，当轴承出现不同故障时，在不同时间尺度上的IMF分量能量均有明显变化，因此可以提取滚动轴承振动信号分解后的IMF分量并计算其能量作为后续LS-SVM的特征输入向量，其计算结果如表2所示，由于篇幅所限，只列举部分样本。

表2 滚动轴承故障诊断特征信息表

在故障特征集构造完毕之后，则是将构造好的故障样本特征集输入给LS-SVM进行轴承的故障辨识。LS-SVM采用1-a-r算法，对于正常状态、轴承内圈损伤、轴承外圈损伤以及混合故障，采用3个两类分类器，例如，当特征样本属于某一分类器时，则该分类器的分类决策函数输出1，否则特征样本输入给下一个分类器继续判断，直到得出诊断结论为止。在采用LS-SVM对滚动轴承测试样本进行诊断的过程中，采用PSO算法对LS-SVM的惩罚参数和核函数参数进行优化选择[10]。在此，参考文献[10]，设定最大进化代数为50代，适应度函数为LS-SVM对轴承故障样本的识别准确率，粒子群中，种群的数目设定为10，粒子的维数为2，学习因子均设定为1.5，其优化过程如图7所示。

图7 粒子群优化LS-SVM的效果图

从图7可以看出，在粒子群优化LS-SVM的过程中，在第2代时就得到了最优的惩罚参数和核函数参数，此时惩罚参数值γ=0.1和核函数参数值α=0.01。图8为采用优化的LS-SVM对滚动轴承测试样本进行诊断的结果统计，图8中圆圈代表故障样本的期望输出，星号代表LS-SVM的实际输出，LS-SVM的期望输出1、2、3、4分别对应于轴承的正常状态、内圈损伤、外圈损伤、混合故障，轴承在不同状态下的样本数量均为40。

图8 优化的LS-SVM实际诊断效果图

从图8可以看出，采用优化的LS-SVM对滚动轴承进行故障诊断，轴承内圈故障的识别率最好，达到了100%，在轴承外圈损伤和正常状态中，均有1个样本被误诊断，在混合故障中，有4个样本被误诊断，其综合故障诊断准确率达到了96.5%。

表3 不同模型的故障诊断精度对比

为了验证LS-SVM进行故障诊断的优良特性，在此还比较了BP神经网络、随机参数的LS-SVM的故障诊断结果。从表3可以看出PSO优化的LS-SVM的诊断结果达到了96.5%，随机参数的LS-SVM的诊断结果次之，达到了88.75%，此时惩罚参数值和核函数参数值均随机设置，γ=0.1，α=20.0；BP神经网络的诊断结果最差，只有84.38%，BP神经网络的训练过程中，由于训练样本数量有限，BP神经网络存在一定程度的欠学习导致最终的诊断结果偏低。综合实验结果表明，对于样本稀缺的情况，相对于BP神经网络、随机参数的LS-SVM，PSO优化的LSSVM其故障诊断模型稳定性最好，诊断精度最高。

5 结论

为了有效提取滚动轴承的振动故障信号并进行故障诊断，本文提出基于EEMD能量熵与优化LS-SVM

的滚动轴承故障诊断方法，实验结果表明采用EEMD处理振动故障信号能够克服EMD分解的模式混叠问题，所提取的IMF幅值能量特征能够更好的揭示故障的本质特征。优化的LS-SVM非常适合于小样本的故障诊断，其诊断方法比传统的故障诊断方法精度要高、收敛速度要快。基于EEMD能量熵与优化的LS-SVM的滚动轴承故障诊断方法能够有效辨识滚动轴承在运行过程中多类故障，可以很好的为滚动轴承的运行可靠性提供判别依据。

[1] 张敏, 崔海龙, 陈曦晖, 等. 基于IMF能量矩和HSMM模型的滚动轴承故障诊断方法[J]. 组合机床与自动化加工技术, 2015(10): 101-103.

[2] 申中杰, 陈雪峰, 何正嘉,等.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J]. 机械工程学报, 2013, 49(2) : 183-189.

[3] 李莎，潘宏侠，都 衡. 基于EEMD信息熵和 PSO-SVM 的自动机故障诊断[J]. 机械设计与研究, 2014,12 (6):26-29.

[4] 任学平, 辛向志, 庞震, 等. 基于IMF熵的多传感器网络融合滚动轴承故障诊断方法研究[J]. 组合机床与自动化加工技术, 2015(6):78-82.

[5] Xianlun Tang, Ling Zhuang, Jun Cai. Multi-fault classification based on support vector machine trained by chaos particle swarm optimization[J]. Knowledge-Based Systems, 2010, (23):486-490.

[6] 徐达, 武新星, 郭磊. 基于最小二乘支持向量机的坦克炮身管剩余寿命预测方法[J]. 装甲兵工程学院学报,2010, 24(1):42-44.

[7] 孙文彩, 杨自春. 结构非概率可靠性分析的支持向量机分类方法[J]. 工程力学, 2012, 29(4):150-154.

[8] Chen Fafa, Tang Baoping, Song Tao. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization[J]. measurement, 2014, 47 (1):576-590.

[9] J Z Wang, S L Zhu, W G Zhao, et al, Optimal parameters estimation and input subset for grey model based on chaotic particle swarm optimization algorithm, Expert Systems with Applications,2011,38 (7):8151-8158.

[10] 陈法法, 汤宝平, 董绍江. 基于粒子群优化最小二乘小波支持向量机的旋转机械故障诊断[J]. 仪器仪表学报,2011, 32(12):2747-2753.

(编辑 李秀敏)

The Roller Bearing Fault Diagnosis Based on EEMD Energy Entropy and LS-SVM

CHEN Fa-faa,b,LI Mianb,Chen Bao-jiab,Chen Cong-pingb

( a. Hubei Provincial Collaborative Innovation Center for New Energy Microgrid;b.Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges University, Yichang Hubei 443002, China)

Aimed at the roller bearing fault vibration signal are non-stationary and nonlinear that are difficult to effectively diagnose, a roller bearing fault diagnosis method based on ensemble empirical mode decomposition (EEMD)and least square support vector machine (LS-SVM) is proposed in this paper. Firstly, the roller bearing fault vibration signal is decomposed by EEMD. Then, each intrinsic mode function components (IMF) is got and these energy are calculated to construct the features vector matrix. Finally, the feature matrix is input into the LS-SVM for the fault mode identification. The validity and feasibility of this method is verified by experiments. The results show that this method based on EEMD energy characteristic and LS-SVM can be more effective for the roller bearing fault diagnosis.

ensemble empirical mode decomposition; least square support vector machine; roller bearing; fault diagnosis

1001-2265(2016)12-0071-05

10.13462/j.cnki.mmtamt.2016.12.020

2016-01-20;

2016-02-27

国家自然科学基金(51405264, 51205230)；三峡大学人才启动基金(KJ2014B007)；湖北省教育厅项目(B2015248)。

陈法法(1983—)，男，湖北秭归人，三峡大学副教授，博士，硕士生导师，研究方向为机电系统动态测试与故障诊断等，(E-mail)chenfafa2005@126.com。

TH166;TG659

A