三自由度并联机构(3SPS-3SRR)的运动学分析

黄 亮，林光春，黄亚太

(四川大学 制造科学与工程学院，成都 610065)

三自由度并联机构(3SPS-3SRR)的运动学分析

黄 亮，林光春，黄亚太

(四川大学 制造科学与工程学院，成都 610065)

针对一种3SPS-3SRR并联机构，运用符号法对该机构进行位置分析及运动学分析建模。构建动、静坐标系，通过矩阵转换对机构建立约束方程，运用sylvester消元方法进行消元得到机构单变元输入输出方程，求得机构位姿的封闭解；在此基础上，对机构建立运动学分析模型，得到了与机构运动相分离的Jacobian、Hessian矩阵，并通过此运动模型可以得到机构输出端任意点的速度及加速度。最后进行实例求解，验证本位置、运动学模型的正确性并通过matlab符号运算及绘图功能得到机构末端执行器的位姿、速度及加速度曲线。得出该求解模型准确、高效，该机构运动特性平滑的结论。

3SPS-3SRR并联机构；位置分析；sylvester消元；运动学分析

0 引言

20世纪60年代，Stewart机构的诞生引起了国际机构学者的广泛兴趣，也标志着并联机器人的诞生，开辟了并联机构的研究新领域。继Hunt[1]首次提出3-RPS并联机构后，国内外学者在该类型机构的构型、位置分析、运动学分析以及工作空间分析等方面做了大量工作。例如：Asada、Lee[2]等设计了多种3自由度并联机构，在运动学及动力学分析基础上，将其运用到某些特定场合。国内的学者对某些具体的机构进行了分析，如黄真等运用螺旋理论对3-RPS机构进行运动学分析并建立动力学模型，通过实例给予验证；鲁开讲[3]等分析了3-RPS机构的约束方程及微分运动的关系，得到了无奇异位的工作空间；张济，姚翔等[4-5]运用符号法对某3自由度可调球面机构进行了位置分析及运动学分析，得到了该机构的8种装配形式及机构末端角速度、角加速度关于时间的曲线；刘善增等[6]对3-RRS并联机构进行了分析，得到机构位姿与约束之间的解析关系。然而，3自由度并联机构种类繁多，位置约束方程及运动学特性具有明显个体差异，对该类机构的特性认识依然不够充分。

作为运动学、力学分析的基础，并联机构的位置分析往往归结为为非线性约束方程组的求解。牛顿拉弗森、同伦连续法、遗传算法[7-8]等数值方法在位置分析中得到了广泛运用，但是数值方法具有初始解难以确定、在线计算时间长、迭代不收敛或者收敛不到预期的解等缺点，基于符号运算的消元方法可以快速得到机构的单变元输入输出方程，达到耗时短、能够实现位置分析解析解的目的。因此符号算法及消元方法在位置分析中的运用具有重要的理论意义及实用价值。

本文基于符号法对一种3SPS-3SRR并联机构进行位置及运动学分析,构建了机构的约束方程进行消元得到机构的单变元输入输出方程进而可得其封闭解，建立速度、加速度模型得到其Jacobian,Hessian矩阵并以动平台作为分析对象得到其速度、加速度曲线。该机构具有并联机构载能力强、刚度大、自重负载比较小的特点、且各分支链成中心对称分布运动学建模及求解具有可复制性、运动特性平滑，具有良好对中性，控制较为简单等优点，在特定场合具有重要用途。

1 机构简介及坐标系的建立

图1为3自由度并联机构(3SPS-3SRR)结构简图。该机构由动平台E1E2E3、静平台A1A2A3、支链AiLiEi及支链BiDiCi(i=1，2，3)组成。支链AiLiEi及支链BiDiCi沿着动、静平台中心所在直线均布。支链在Ai、Ci、Ei点的运动副均为球面副，在Bi、Di为转动副，且AiBi所在的直线与相应位置支链的转动副轴线垂直。Li为三条驱动杆，通过其杆长变化可以改变机构位姿。

图1 3SPS-3SRR并联机构结构简图

在并联机构位置分析建系过程中，通常选择动平台中心作为动坐标系原点，在本机构中为了尽量减少位置分析变量的个数，按以下方法建立坐标系：以右手定则在静平台上建立静坐标系T0，如图所示为坐标系O-xyz，其原点为静平台中心，z轴垂直于平面E1E2E3，x轴沿B1A1方向；在动平台建立动坐标系T1，如图为坐标系O1-x1y1z1，C1为该动坐标系原点，z1轴垂直于动平台指向上方，x1轴沿C1E1方向。按此建立的动坐标系原点在y向分量恒为0，从而达到减小位置分析变元的目的。

2 位置分析及求解模型

根据建立的坐标系，可以分别将Ai、Bi在静坐标系T0下标出，也可将Ci、Ei在动坐标系T1下标出。再根据坐标转换，在T0系下得到动平台上特征点坐标式，进而建立约束方程，求解可以得到动平台位姿，从而达到位置分析的目的。

2.1 位置约束方程

设静平台上A、B点距其中心O点半径分别为ra、rb，动平台上C、E点距动平台中心为rc、re，三个驱动杆杆长为L1、L2、L3。

设φ、θ、ψ为动平台三个欧拉角，平移向量为R0=(x0,y0,z0)T，按zyz坐标矩阵转化形式进而可以得到得到齐次变换矩阵M[9]，

(1)

记cφ=cosφ,sφ=sinφ,cθ=cosθ,sθ=sinθ,cψ=cosψ

sψ=sinψ则:e11=cφcψ-cθsφsψ,e12=-cφsψ-cθcψsφ,

e13=sφsθ,e21=cψsφ+cφcθsψ,e22=cφcθcψ-sφsψ,

e23=-cφsθ,e31=sθsψ,e32=cψsθ,e33=cθ。

通过M，可以得到T0下的坐标矩阵。对驱动杆，可以建立杆长约束方程：

(2)

由机构结构限制，对C点可以建立平面约束方程：

(3)

2.2 位置约束方程封闭解模型

交替使用加减及代入消元法，消去式(2)、式(3)中线性变元，得到：

3rCsin(φ+ψ)(1+cosθ)=0

(4)

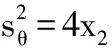
(5)

将式(5)中各式分别代入关于φ、θ的非线性方程组,提取分子得到多项式方程。

(6)

将式(6)改为矩阵形式，令其Sylvester结式[10]为0消去x2，得到：

(7)

式中系数是机构结构及输入杆长的函数。通过matlab符号运算可以得到系数的符号表达式。求解式(7)，将所得结果回代，可以分别得到各变元的解。

3 3SPS-3SRR并联机构运动学分析

3.1 机构运动影响系数

机构影响系数是由Tesar提出的，为表征机构特性的参量提供了显性表达式。由影响系数法建立的矩阵将机构从运动中分离出来，可以将机构特殊位形、机构驱动空间以及机构灵活性、各向同性等归结为对其影响系数矩阵的分析，特别是Jacobian、Hessian矩阵在机构运动学的运用，为机构速度、加速度分析提供了求解方法。

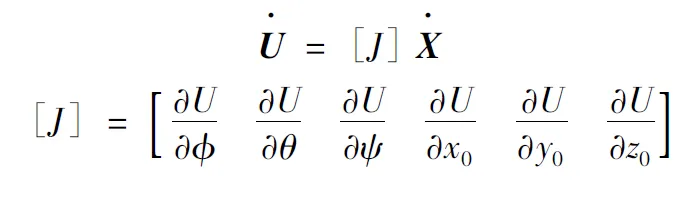
(8)

对式(8)的一阶导数：

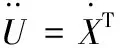
(9)

3.2 机构速度分析

式(2)、式(3)构建的约束方程可以确定本处并联机构的位姿，得到：

(10)

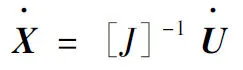
(11)

对于并联机构动平台上任一点

(12)

将式(11)代入式(12)可以得到动平台上任一点线速度。

3.3 机构加速度分析

直接对式(10)求二阶导数，得到机构二阶运动影响系数：

(13)

(14)

对于动平台上任一点P[x,y,z]T，

(15)

式(15)可以得到输出末端(动平台)任一点线加速度。

4 并联机构运动学实例求解

4.1 位置求解实例

并联机构结构参数ra、rb、rc及re分别为500、410、480及500，三驱动杆长度变化范围分别为330～460。

取驱动杆长L1=363、L2=400、L3=440，代入式(7)，得到x1的64组解，筛选得到其中10组实数解，见表1。

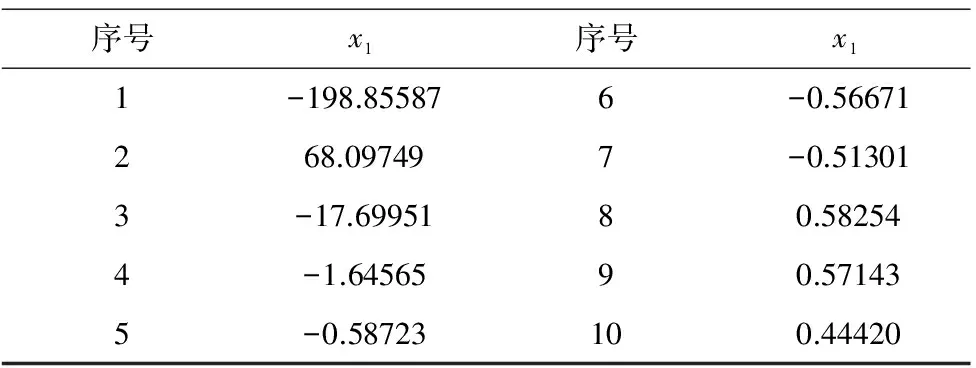
表1 sylvester消元后单变量方程10组实根

将表(1)中数据分别回代求解出机构位姿的32组实解。

4.2 运动学求解实例

记杆长与时间变化函数分别为：L1(t)=395+sint，L2(t)=395+sint，L3(t)=395-sint，取时间t的变化范围为(0～4π)，步长为π/50。将机构结构参数、驱动杆变化规律及动平台位置代入式(11)、(14)，可以分别得动平台位置变化速度、加速度，通过matlab编程，绘制其曲线见图2、图3。

(a)动平台姿态速度 (b)动平台位置速度图2 动平台速度曲线

(a)动平台姿态加速度

(b)动平台位置加速度图3 动平台加速度曲线

取动平台质心P(平台中心)代入式(12)、(15)得到质心各向线速度v、加速度a，绘制其曲线图，见图4。

(a)动平台P点速度

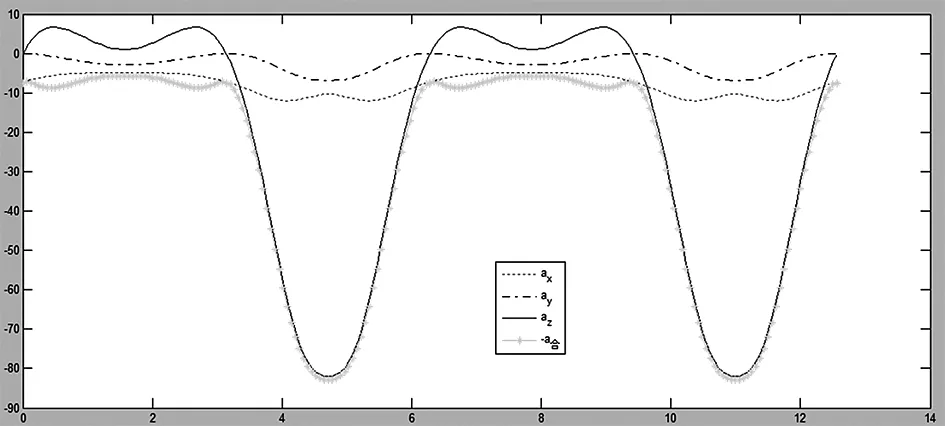
(b)动平台P点加速度图4 动平台质心速度、加速度

由动平台位姿曲线，在机构处于特殊姿态时，此瞬间会对平台产生较大冲击，但是在运行一般形位，动平台展现出良好的运动特性，并且在水平方向的位移、速度、加速度变化微量，呈现出良好的对中特性。在一些需要对中性的特殊场合具有重要意义。

5 结论

(1)对一种三自由度平台型并联机构建立了位置、运动学分析模型。运用结式消元方法得到了机构位姿封闭解，构建了Jacobian、Hessian矩阵，并基于matlab符号运算得到其符号显式。本模型的求解分析过程对于平台型并联机构具有普适性。

(2)采用sylvester消元法对机构位姿的非线性约束方程组进行消元，得到了位姿的解析解，降低了并联机构的位姿方程的求解难度，避免了数值法初值难以确定及耗时长的不足。

(3)得到了该并联机构输出端的速度、加速度曲线。得到的输出端质心在水平方向的速度及加速度相对于竖直向的分量较小，输出端具有较好的对中性，且平滑性较好，冲击小，再加之该机构具有承载能力强、结构对称、控制较简单等优点，在一些特殊场合，该机构具有重要作用。

[1] HUNT K H.Structural kinematic of in-parallel-actuated robot arms[J].Journal of Mechanisms,Transmission and Automation in Design,1983(105):705-712.

[2] LEE K M,SHAH D K.kinematic analysis of a three degrees of freedom inparallel actuated manipulator[J].IEEE Journal of Robotics and Automation,1988,4(3):354-360.

[3] 鲁开讲,牛禄峰,刘亚茹,等.3-RPS并联机构奇异位形及工作空间研究[J]. 农业机械学报, 2007,38(5):143-146.

[4] 张济,林光春,徐礼钜,等.可调球面三自由度并联机构的位置分析与动态仿真[J]. 机床与液压,2007,35(6):176-179.

[5] 姚翔,林光春,豆依玲.三自由度可调并联机构的位置与运动学分析[J]. 组合机床与自动化加工技术, 2015(3):59-61.

[6] 刘善增,余跃庆,佀国宁,等.3自由度并联机器人的运动学与动力学分析[J].机械工程学报,2009,45(8):11-17.

[7] 李庆扬,莫孜中,祁力群.非线性方程组的数值解法[M].北京:科学出版社,1987.

[8] 豆依玲,林光春,姚翔.可调球面5R机构多任务轨迹综合的遗传算法优化[J].制造业自动化, 2014,36(12):107-111.

[9] 黄真,赵永生,赵铁石.高等空间机构学[M].北京：高等教育出版社,2006.

[10] 李盛前,谢小鹏.基于旋量理论和Sylvester结式法的6自由度机器人逆运动学求解分析[J]. 农业工程学报,2015,31(20)：48-54.

[11] 甘东明.空间机构的运动学分析及新型并联变胞机构的设计[D].北京：北京邮电大学，2009.

[12] 张忠海,李端玲.一种平面并联机构位置正解分析的共形几何代数及Sylvester结式方法[J]. 北京理工大学学报,2014,34(3):241-244.

[13] 谢存禧,李琳.空间机构设计与应用创新[M].北京:机械工业出版社,2007.

[14] 黄忠霖,黄京.MATLAB符号运算及其应用[M].北京:国防工业出版社,2004.

(编辑 李秀敏)

Kinematics Analysis of 3 SPS-3 SRR Parallel Mechanism

HUANGLiang,LINGuang-chun,HUANGYa-tai

(SchoolofManufacturingScienceandEngineering,SichuanUniversity,Chengdu610065,China)

Themodelofkinematiccanbeacquiredbasedonsymbolicmethodconcerningathree-DOFparallelmechanism.Firstly,setupstaticanddynamiccoordinatesystem,establishedtheconstraintequationsthroughmatrixtransformationinthispaper.Thenconvertedthesimplifiedequtionsintopolynomialequtions.Theclosed-formexpressionofconstraintequtionswouldbegotbysylvesterelimination,innext.Onthisbasis,researshedkinematicscharacteristicsoftheparallelmechanism,gottheJacobianHessianmatrixsthatareindependentofthemotionsofactuatingarms.wecanalsogettheterminalarbitrarypoint’svelocityandaccelerationthoughthemodel.Atlast,verifiedthemodelhadbeenprovedasanefficieneandaccuratemethedbycalculatinganexample.Meanwhile,drewtheterminalcentroidposition,velocityandaccelerationcurvethoughthemodelprogrammingontheMatlab.Ingeneral,themethedofthemodeliscorrect,efficient;thekinematicscharacteristicofthemechanismissmooth.

3SPS-3SRRparallelmechanism;positionanalysis;kinematicanalysis;sylvesterelimination

1001-2265(2016)12-0056-04DOI:10.13462/j.cnki.mmtamt.2016.12.016

2016-02-25；

2016-03-30

黄亮(1990—)，男，四川南充人，四川大学硕士研究生，研究方向为机构及机器人学，(E-mail)1471556247@qq.com。

TH112；TG

A