Chebyshev多项式及其插值法在函数求导中的应用

周 晶，张红芹

(吉林农业大学 信息技术学院，长春 130118)

Chebyshev多项式及其插值法在函数求导中的应用

周 晶，张红芹

(吉林农业大学 信息技术学院，长春 130118)

为了更精确地用插值函数的导数逼近复杂函数的导数，本文基于Chebyshev多项式和最小零偏差定理提出了一种应用Lagrange插值求复杂函数导数的新方法。我们首先以n+1次Chebyshev多项式的零点作为插值节点进行Lagrange插值，进而用插值函数的导数值逼近被插值函数的导数值。误差分析和数值算例表明本文所提出的方法在复杂函数求导中取得了良好的效果。

Chebyshev多项式；插值；最小零偏差；函数求导

0 引言

函数逼近论是近代数学的重要研究方向，其主要思想是用简单可计算函数对一般复杂函数进行近似逼近。一种非常重要的逼近方法就是插值逼近，如代数多项式插值、三角多项式插值、样条函数插值等，而且计算数学的其他理论如数值微分、数值积分等都是以插值理论作为基础展开研究的[1-2]。

目前关于对原函数的导数的逼近问题，通常采用样条插值函数的导数进行逼近。但由于Lagrange插值或Newton插值可能出现Runge现象，因此应用一般的Lagrange或Newton插值函数的导数逼近原函数的导数时可能会出现收敛性的问题。而Chebyshev多项式零点插值方法可以克服Runge现象，并可对任意变化的函数得到更高精度的近似[1-2]。本文给出一种应用Chebyshev多项式的零点作为插值节点进行插值函数求导逼近原函数导数的方法，研究表明应用此方法可以得到原函数导数的最佳一致逼近多项式。

1 Lagrange插值与Chebyshev多项式[2-7]

1.1 Lagrange插值

插值多项式为

余项为

其中ωn+1(x)=(x-x0)(x-x1)…(x-xn)。

1.2 Chebyshev多项式

Chebyshev多项式是一类特殊的n次代数多项式，由于其零点(通常称为Chebyshev节点)用于多项式插值时，相应的插值多项式能够最大限度的降低龙格现象，因此切比雪夫多项式在函数逼近理论中有着非常重要的应用。

定义(Chebyshev多项式)设x是区间[-1,1]上的任意实数，n∈N，则称多项式

Tn(x)=cos(narccosx)，为n阶Chebyshev多项式。

由方程易得n+1阶切比雪夫多项式的n+1个零点为：

引理[7](最小零偏差定理)设x0,x1,…,xn是Chebyshev多项式Tn+1(x)的n+1个根，记ωn+1(x)为

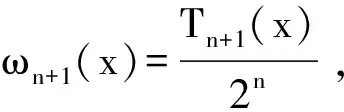
设f(x)∈Cn[-1,1]为被插值函数，则根据最小零偏差定理，其插值节点选为切比雪夫多项式的零点时所得插值函数最佳一致逼近函数f(x)。

2 误差分析

我们应用Chebyshev多项式的零点作为插值节点，用Lagrange插值函数的导数逼近原函数的导数，并给出了误差分析。

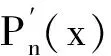
|Rn′(x)|

证明：当x=xi时，有：

当x≠xi时，有：

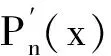
证明已知插值区间为[a,b]，为了应用Chebyshev多项式插值法，需通过简单变换归一化到区间[-1,1]。因此作变换如下，设：

x∈[a,b],z∈[-1,1]。则

ωn+1(x)=(x-x0)(x-x1)…(x-xn)

因此，Chebyshev多项式Tn+1(z)的零点为：

则相应多项式Tn+1(x)的零点为：

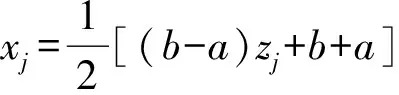
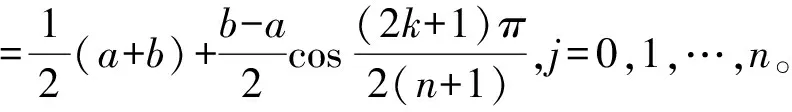
将xj(j=0,1,…,n)作为插值节点,可得误差为：

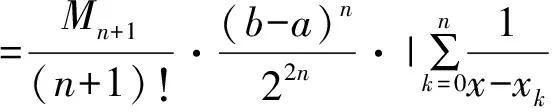
3 数值算例

P6(x)=-7.6389x6+8.6749x5+4.7438x4-5.681x3-0.7876x2-0.8364x+1.0666。

相应的导数为：

P6′(x)=-45.8334x5+43.3745x4+18.0752x3-17.043x2-1.5752x-0.8364。

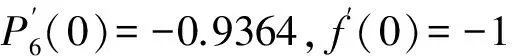
综上可知，Chebyshev多项式在插值函数的求导中是非常适用的，并且对于复杂函数的求导可以更加容易的得出结果。

[1] 王仁宏.数值逼近[M].北京:高等教育出版社,2000.

[2] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008.

[3] 肖蒙,李军.切比雪夫多项式及其插值法在检测中的应用研究[J].自动化与仪器仪表,2006(3):13-16.

[4] 徐晓芳,蔡静.切比雪夫多项式零点插值与非线性方程求根[J].湖州师范学院报,2016,38(2)：1-5.

[5] 化小会,张秋生.切比雪夫多项式在代数信号处理中的应用[J].西南师范大学报,2016,41(5)：108-114.

[6] 尤文坚,梁兵,李萌军.基于切比雪夫算法传感器特性参数拟合系统[J].传感器及非电量检测技术,2013,36(2)：92-107.

[7] 王倩,阿不都热西提·阿不都外力.用最小零偏差定理逼近多项式函数的低次公式及其Matlab程序设计[J].石河子大学学报,2005,23(2)：140-142.

责任编辑：程艳艳

Application of Chebyshev Polynomial and Its Interpolation Method in Function Derivative

ZHOU Jing, ZHANG Hongqin

(College of Information Technology, Jilin Agricultural University, Changchun 130118, China)

In order to accurately make the approximation of interpolation function derivative to complex function derivative, this paper presents a new solution to complex function derivation by Lagrange interpolation based on Chebyshev polynomial and minimum zero deviation. We take the zero point of Chebyshev polynomial with n+1 degree as the interpolation node to make Lagrange interpolation, and then use the derivative value of interpolation function to approximate the derivative value of primitive function. The error analysis and numerical example show that the method presented in this paper achieves a better effect in complex function derivation.

Chebyshev polynomial; interpolation; minimum zero deviation; function derivation

2016-07-16

吉林农业大学科研启动基金资助项目(2015043)

周晶(1980-)，女，吉林德惠人，讲师，硕士，主要从事从事应用数学方面研究；张红芹(1971-)，女，河北定县人，回族，讲师，主要从事计算数学方面研究。

O241

A

1009-3907(2016)12-0056-03