基于非线性电路的数据文件加密方法实现
2016-02-06李明晶王曼玮
李明晶,王曼玮,王 盈
(长春大学 a.电子信息工程学院;b.研究生部,长春 130022)
基于非线性电路的数据文件加密方法实现
李明晶a,王曼玮b,王 盈b
(长春大学 a.电子信息工程学院;b.研究生部,长春 130022)
混沌在非线性科学中是一个很重要的组成部分,由于它具有确定性、有界性、对初值的敏感性、长期不可预测性等固定特性,使其混沌理论及其应用研究获得了巨大的发展。在混沌保密通信、数据加密、流体混合等领域,成为大家普遍所接受的方法及其应用重点。由于混沌信号明显的宽带白噪声特点,可根据非线性动态系统产生并且很容易进行控制。动态系统的不同初始状态下,所产生的混沌信号相互之间不但正交且独立。因此,混沌信号在保密技术方面中得到了广泛的应用。
混沌;非线性; 数据加密
0 引言
在信息化、网络化时代,人们手中的数字化信息,可以借由很多种方式传播开去。数据文件就是传达信息的媒介之一,网络上的数据文件很多是要求发送方和接收方都要进行加密通信,可以看出当今社会对信息的安全保障要求之高。而混沌序列,具有对初始条件和混沌参数敏感等特征,近些年来在加密领域得到了广泛的应用。使用必要的算法将信息进行加解密,实现信息的保护。
在通信技术中,应用混沌序列信号进行扩频、调制、加密等手段,不仅仅是奠定了混沌保密通信在未来发展中的广阔前景,更使通信系统在实际运用中保留了许多混沌信号的特点。然而,凡事都有双面性,正是由于混沌信号在系统初始状态的高度敏感性,使其作为通信信号载体进行同步传输具有一定的困难性,所以需要通过保证通信系统中收发双发同步来实现。
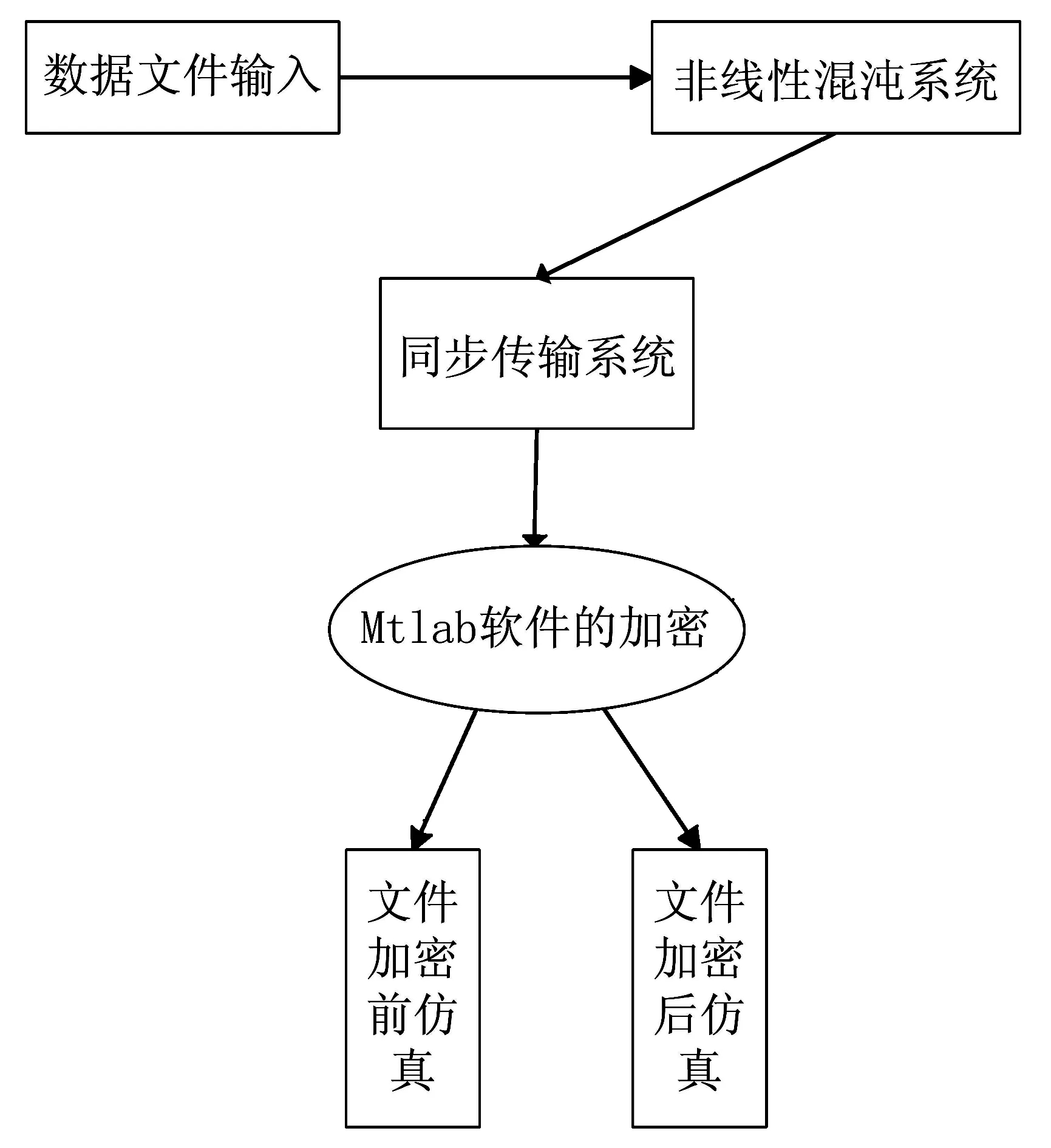
图1 系统结构框图
1 总体设计方案
1.1 设计主要思路
本课题的主要设计内容是构造非线性混沌电路,以此利用混沌电路实现通信同步。基于混沌的数据文件加密算法及实现,即设计一个在MATLAB环境下,基于混沌的数字文件加密系统分析加密的结构特点,完成加密的理论与变换,选择一个加密原理。对任意输入的文件数据进行仿真实验,实现其方法的应用。
拟采用的实施方案:
(1)构造非线性混沌电路;
(2)利用非线性电路实现通信同步;
(3)利用MATLAB软件对文件加密,做出加密前和加密后的仿真分析。
根据混沌序列的自身特点,借助MATLAB编程语言,编写适当的算法信息进行加解密,实现对秘密消息的加密保护。系统结构框图如图1,第一步就是推导状态方程,在对其平衡点进行稳定性分析之后,借助MATLAB软件,编好程序,再进一步仿真,最终得到非线性混沌电路。
1.2 基于非线性电路的图像加密方法
Logistic映射是一个标志性的、有确定形式特征的非线性简洁迭代方程。虽然整个系统中并没有任何随机因素,最终却显示出类似于完全随机、对初始条件和混沌参数敏感的现象。因此,本设计中,拟采用Logistic映射迭代出混沌序列,置乱了源图像的像素点,使得加密效果得以产生。对比结果是比直接加密图像的效果更好。基于Logistic映射与排序变换的图像加密算法,是在利用混沌映射中混沌信号对的初始值的敏感性和伪随机性,以重新排列混沌序列这种方式,来获取已被置乱的图像的地址变换码。又因为这样排序所存在的不规则性,所获得到的新的混沌图像置乱后,比一般算法更具安全性。利用这种算法实际进行仿真实验的操作,分析数据之后看出,像素置乱算法具有良好的图像文件加密性能。
1.3 图像加解密的仿真
人类数据信息中,图像信息应用最为广泛,所以实验运用异或运算将数据进行隐藏,连续使用同一数据对图像数据两次异或运算图像的数据不发生改变,利用这一特性对图像信息进行加密保护。用户输入的密码必须是0-1之间的任何一个数据,进行加密过程中,加密的程序与解密的程序输入的密码必须一致才能正确解密图像。
2 基于混沌电路的图像加密方法
2.1 图像的加密技术
通过电子电路来产生非线性体系统,我们可以借助设备来进行相关数据的测量记录。比如示波器:显示混沌系统的电压数据,观测其电流波形,比较相位图。而功率谱图,我们可以利用频谱分析仪进行进一步测量分析。各类非线性动力学中的相关参数数据,对于现在这个信息化、网络化的时代来说,很方便,很快捷,所以混沌电路的研究价值很高。随着信息化社会的进步,混沌电路通信、数据文件保密通信等,不论是系统芯片,还是高精度的混沌元件,在研究设计上,都不再是难事,并以此来构造和测试各种混沌分析软件。
传统意义中的加密算法,基本都不适合对图像进行加密,因为图像中所包含的信息量都很大。传统图像加密算法都是根据位置置乱,如变换。这些加密算法都具有加密速度快的优点。但是,其技术安全性完全依赖于算法的安全性,使之很难满足于现代加密系统的硬性要求。从对图像数据处理的方式来分类,那么技术层面上的加密是由位置置换、值的变换以及组合形式三部分组成。假若从图像的像素信号处理的这方面来看,则有空间域、频率域这两种算法。
2.1.1 Logistic加密算法
置乱变化加密技术是图像加密中最基本的加密技术之一,也是一般的图像安全技术中最为基础的技术。在其本身来看,图像像素点置乱就是对图像的像素数据块做一次不同于原图像像素现有排列的全排列。
2.1.2 Logistic加密算法的原理
在加密技术发展初期,数字图像加密主要是通过使图像像素位置发生变换来完成加密的。也就是说,将源图像矩阵中的像素随意全排列,直到出现渐变效果,新的图像将完全不同于原图像,使这个图像数据本身成为类似于随机数据的方式而达到加密的目的。
数字图像的置乱变换,只要都符合映射的条件,一一对应,即可以从一维、二维、三维以及高维变换来分析,也就是可逆变换。既能由正变换对图像进行加密的工作,反过来,也可以利用逆变换,对已经加密后的图像进行完整解密。
一维变换中,首先需要做的是对源图像逐行扫描,得到对应的一维向量。然后再重新整合、排列其中元素,最终重新根据扫描顺序,得到新的图像数据矩阵,成为加密后的图像。
二维变换中,先运用数学变换把二维图像像素的坐标进行一个整体变换,接下来按像素的坐标的对应关系将图像像素点重新构成新一个图像数据矩阵,成为加密图像。
三维变换中,将源图形分成(n+1)×n的块,同样对源图像逐行扫描,得到对应的一维向量。再重新排列、规则变换图像像素点坐标,最终重新根据扫描顺序,得到新的图像数据矩阵,得到加密后的图像。由变换域的置换这方面来说,存在基于以下三种空间的置乱变换:位置、色彩和频率,也就是由像素位置亦或是色彩的不同变换来达到置乱图像,最终加密的目的。
2.1.3 Logistic加密的变换特征分析
恢复置乱后的图像,重新得到原图像,也就是解密。原图像与加密后的图像,它们必须要是可逆或能够通过变换恢复到初态的周期性的关系。不同组合的密钥,是决定置换的结果不尽相同的关键。所以要保证密钥空间要尽可能大。
一般来说,我们是在空域研究图像置乱技术的,在这个阶段中会有很大概率改变图像中像素间的关系,编码时,就会在一定程度上降低压缩率。所以,如何将图像置乱加密和图像压缩两大项可以更加有效地结合在一起,在目前来看是主要研究方向。
2.1.4 Logistic加密置乱程度的度量
关于置乱变换的优缺点,除上述的要求以外,我们也可以按照置乱度来进行定量。图像相邻像素间的平均灰度差是我们衡量置乱通常所用的手段。经过大量对比分析,图像置乱前后,位置置乱、灰度置乱都看出原图像平滑区域分布较多,像素值与像素值之间相较于相邻区域来说,很稳定,没有太大的区分(除纹理区外)。而置乱后的结果与之相差极大,不同的像素值间,像素点随机交错,大范围内像素值趋平的区域不复存在了。由此,相邻灰度差的置乱就此出现。实际上也就任意像素与其所相邻的像素像素值之间的差值越大,置乱图像效果越好。
2.2 基于混沌的图像加密技术
2.2.1 混沌图像加密系统模型
借由具有非周期性和伪随机这些特点的混沌序列,同初态明文序列依次异或,最终达到加密的效果,这就是混沌加密。英国数学家Matthews最早提到混沌流密码,解决了作为序列密钥流生成器,Logistic混沌映射所存在的问题,以加大密钥空间。
混沌映射、扩散函数和重复次数是加密系统的安全性的关键点。在系统中,明文图像要达到密文图像的效果,就需要借由混沌置乱、扩散和反复迭代加密。在诸如此类的混沌映射因素外,还有置乱的次数也与密码混沌加密系统的安全性有着密切相关的联系。假若置乱的次数越多,每次迭代的密钥又不同,混沌加密系统秘密性越高。

图2 图像混沌加密的模型
2.2.2 基于Logistic映射的图像加密算法
数字图像的置乱加密算法的目的:利用相关非线性变换来替换原有的图像矩阵,让图像完全与原图像不同。即使图像是一个二维矩阵,借助混沌序列,调制由像素值组成的一维向量,依旧能够将二维矩阵变为一个一维向量,实现加密。
2.3 Logistic映射加密示例与分析
Logistic映射,目前应用非常广泛的,由映射特征所做的相关算法。假设,某单一种类的昆虫,在固定一段范围内繁殖时,数量上其子代大大超过亲代,我们就说,于子代繁殖出之后,亲代的数量几乎就能够无视掉了。
比方说:设Mi是某种昆虫第i年的个体总数,其中Mi与i有关,i的取值为1,2,3,...而一维Logistic映射可以有如下数学表示:
M(1)iii=μ(M-M),其中μ为控制系数。
Logistic映射的定义式如下:
Xk+1=uxk(1-xk)
(1)
其中,0﹤μ﹤4为分叉参数,x∈(0,1)。当3.569456﹤μ﹤4时,logistics映射工作状态一直处于初始状态。即:Logistic映射的作用下,初态所产生的序列{以k=0,1,...),是非周期性的、不收敛的,同时异常敏感于初始值。于(0,1)中随机取一个混沌置换初值x0,多次置乱,最后用混沌密码序列加密各个像素值。
2.3.1 加密技术设计原理
运用异或运算方式将数据进行数据隐藏,持续坚持使用同一数据分别对图像数据进行两次异或运算图像的数据一定不会发生改变。利用上述所发现的这一特性对图像信息进行加密保护。用户输入的密码必须是在0~1 之间的任何一个数据,并对其进行加密,并且加密的程序与解密的程序输入的密码必须完全一致才能正确解密。
加密程序核心代码如下:
fori=1:N-1 % 进行N-1 次循环
m(i+1)=4*m(i)-4*m(i)^2; % 循环产生密码
end
m=mod(1000*m,256); %1000*m除以256 的余数
m=uint8(m); %强制转换为无符号整型
n=1; %定义变量n
fori=1:a
for j=1:b
e(i,j)=bitxor(m(n),x(i,j)); % 将图像信息藏在e(i,j) 矩阵中进行
异或运算
n=n+1;
end
End
2.3.2 运行结果与分析



3 加密算法的MATLAB仿真步骤
对图像进行加密算法的仿真是一个应用MATLAB语言程序编写然后再执行的过程。程序将利用MATLAB软件提供的丰富的函数,在命令窗口进行程序的运行来实现仿真。
3.1 MATLAB预处理
第一步,是MATLAB对原图像的图像数据做出灰度处理的部分,调用MATLAB软件、并顺利完成接下来的其他运作。
(1)为了让它成为矩阵数组,我们一开始要做的是读取彩色图像数据。
(2)将原始的图像转换成灰度图像。因为考虑到本设计只对灰度图像做加密解密算法的仿真,所以需要存在这一部分的预先准备。
3.2 显示图像
置乱变换加密图像的这样一种算法,即随机排序,变换图像的像素点坐标。
为了更好地演示图像置乱变换的原理,我们选取Logistic映射来做置乱变换,进行MATLAB仿真。首先在256X256像素大小,即灰度值为255的白色图片正中间,选取8X8的像素点,令其灰度值为0,接下来分别做两轮置乱加密变换,最终呈现的就是置乱加密后的图像。
3.3 图像的加密
本设计中所描述的加密算法,是借由图像分组,进行一系列运算变换,整个图像就好比是一个大的数据块,多次的置乱可以转换明文的统计特征,最终达到加密的算法。在诸如此类的混沌映射因素外,假若置乱的次数越多,每次迭代的密钥又不同,混沌加密系统秘密性越高。通过两种方法的交互使用,最后就能够以循环次数比较少的情况下迅速加密。本部分为图像加密过程,主要是对图像做加密处理。
(1)任意混沌序列作图像加密算法中的密钥(例如:猫映射、Logistic映射、Henon映射),相对应的混沌映射参数。(本设计中我们应用的是Logistic映射)
(2)进行图像像素位置的置乱变换。
(3)再继续重复操作上述的置乱变换。
根据要求,选择任意点作为它的初态,所得到的混沌的实值序列实际上是不可以拿来作图像加密工作的。原因是,这个混沌实值序列的值不一定会在像素灰度值的取值范围内。所以,首先要做的是预先处理混沌实值。介于混沌系统存在非周期性、随机性以及敏感性的特点,需要混沌序列上任意元素值做出取整浮点数的操作,以保证能够有相应的位数。
3.4 显示图像
比较加密前图像与加密后图像的效果。
3.5 图像解密
这一部分则是第三步(加密过程)的逆过程,因为映射具有一一对称性,所以解密的步骤与加密过程完全相反,可是密钥值(即混沌参数和置乱扩散参数)必须完全一致,否则无法对图像进行解密操作。
解密过程也就是由加密矩阵的密钥,产生解密矩阵,把加密后的图像再次位置置乱的算法逆运算,得到加密图像。再将加密图像通过解密程序解密,形成最后的解密图像。
4 结语
在这次基于非线性电路的数据文件的加密解密及仿真方法的实现研究中,我们运用了MATLAB,开发项目的大量时间是对图像的加密、对加解密后图像进行仿真比较等方面,它为我们提供一个强大的分析能力和对动态系统的模型化和仿真。实验结果表明:原图加密,方针实际操作后所呈现出的新图像,完全不同于原图,成功地完成了对图像数据的加密的目的。此混沌序列算法非常适用对图像数据的加密,进而实现对数据的保密,在网络传输中能够很好地保护图像数据不被第三方轻易获取其内容,实现数据的隐藏保护。
[1] 陈鲁生,沈世镒.现代密码学[M].北京:科学出版社,2002.
[2] 苏莉萍.基于混沌的图像置乱加密算法及MATLAB的实现[J].装备制造技术,2007(8):79-81.
[3] 叶群.混沌及其在图像加密中的应用研究[D].长沙:湖南师范大学, 2009.
[4] 高铁杠,陈增强,袁著祉.混沌系统的混合同步及其在安全通信中的应用[J].通信学报,2005(3):21-24.
[5] 赵百超.基于混沌理论的信息加密算法研究[D].沈阳:东北大学,2001.
[6] 周霖.基于混沌的图像加密及其DSP实现[J].广东工业大学学报,2014,32(1):45-46.
[7] 毕伟光.吴爱国.BI Weiguang.WU Aiguo 一种用于混沌保密的新型混沌信号产生电路[J].信息安全与通信保密,2007(5):131-132.
[8] 吴健珍,谢剑英.基于混沌的保密通信方案的研究[J].通信技术,2003,135(3):87-89.
[9] 权安静,将国平,左涛.基于Logistic映射的分组密码算法研究及其应用[J].东南大学学报(自然科学版),2004(S1):11-14.
[10] 秦红磊.混沌置换网络的设计及其硬件实现[J].电子技术应用,2001,27(6):54-56.
责任编辑:程艳艳
Implement of a Data File Encryption Method Based on Nonlinear Circuit
LI Mingjinga, WANG Manweib, WANG Yingb
(a. College Electronic Information Engineering; b. Graduate Department, Changchun University, Changchun 130022, China)
Chaos, with its fixed features such as certainty, bounded property, susceptibility to initial value, long-term unpredictability and so on, is a very important part in nonlinear science, letting the research on its chaos theory and application have a great progress, which becomes a common method and an applied focus in the fields of security communication in chaos, data encryption and fluid mixing. Due to the obvious characteristic of wide band white noise of the chaotic signal, it is easy to control according to the nonlinear dynamic system. Under different initial states of dynamic system, the generated chaotic signals are mutually independent and orthogonal. Therefore, chaotic signal has been widely used in security technology.
chaos; nonlinear; encryption data
2016-09-12
吉林省教育厅科研项目(吉教科文合字[2014]第302号)
李明晶(1977-),女,吉林公主岭人,副教授,博士,主要从事光电跟踪测量和图像融合算法研究;王曼玮(1993-),女,江苏南京人,硕士研究生,主要从事控制工程研究。
TP309
A
1009-3907(2016)12-0015-06
