一种约束的改进可能性C均值聚类方法研究

肖振球，曾文华

( 1.嘉应学院计算机学院，广东 梅州 514015；2.厦门大学软件学院，福建 厦门 361005)



一种约束的改进可能性C均值聚类方法研究

肖振球1，曾文华2

( 1.嘉应学院计算机学院，广东 梅州 514015；2.厦门大学软件学院，福建 厦门 361005)

【目的】 针对改进的可能性C均值聚类方法(IPCM)运算效率低，难以处理复杂数据结构的问题，提出了一种约束的改进可能性C均值聚类方法(CIPCM).【方法】 CIPCM方法采用多项式核将特征向量映射到一个隐性特征空间，便于处理复杂的数据结构；引入两个成对约束集合，降低聚类迭代次数，提高运算效率和抗干扰能力.实验采用国际公认的UCI公共测试数据集，并用错分率指标评测了目标分类性能.【结果】 CIPCM方法的聚类错分率低，对噪声的鲁棒性强.【结论】 CIPCM运算效率比高于改进可能性C均值聚类方法.

聚类；C均值；模糊C均值；可能性C均值；改进的可能性C均值

聚类是一种无监督的分类方法，依据各类目标之间的相似性自动进行分类，广泛应用于数据挖掘、模式识别、图像处理等领域[1].现有聚类方法主要分为四类：基于划分的聚类方法、基于分层的聚类方法、基于密度的聚类方法和基于网格的聚类方法，目前应用最为广泛的是基于划分的聚类方法[2].

划分可以分为硬划分和软划分两类，硬划分是将所有对象都严格地划分到某一个类别中去，也即分类后的隶属度只能0或1.C均值(C-means)[3]是目前应用最为广泛的基于硬划分的聚类方法，其算法实现简单，运算效率高，在图像分割、目标跟踪等领域都已有成功应用.然而，现实世界中许多对象是存在重叠的，难以严格地划分到某一类别，于是出现了模糊聚类方法，这是一种软划分方法，划分后的隶属度在0～1之间，可以通过最近邻原则转换为硬划分.模糊聚类的代表性方法是模糊C均值(fuzzy c-means，FCM)聚类方法[4]，模糊C均值聚类方法通过引入模糊权重指数，实现对象的模糊分类，几何意义直观且运算效率高.但该方法对隶属度的约束较为严格，导致算法对噪声较为敏感.为了克服FCM算法对噪声敏感的问题，文献[5]放宽了隶属度约束条件，修正了目标函数，提出了一种可能性C均值(possibilistic C-Means，PCM)聚类算法.IPCM方法通过放松隶属度约束条件，可以降低噪声对聚类的不利影响.但PCM算法对初始凝聚点比较敏感，而且聚类原型可能趋同.针对PCM算法的缺陷，文献[6]改进了PCM算法，改进后的算法称之为改进可能性C均值(improved possibilistic C-Means，IPCM)算法.该方法将FCM和PCM方法相结合，是目前处理部分重叠和噪声数据的有效聚类方法.但该方法处理球状类型的簇时，运算效率严重下降，而且不能处理复杂的数据结构.文献[7]则根据基因表达数据分析特征，提出评价方案和改进策略，该算法提取基因特征点清晰，但也面临自动分析缺陷问题.

针对IPCM方法运算效率低和难以处理复杂数据结构的问题，本文提出一种约束IPCM方法，记为CIPCM(constrained improved possibilistic c-means)方法.本方法采用多项式核将特征向量映射到一个隐性特征空间，便于处理复杂的数据结构；通过引入必须相连和不可相连两个成对约束集合，来提高运算速度和降低噪声干扰，最终提高聚类准确率.

1 模糊聚类方法

模糊聚类是解决对象重叠问题的有效方法之一，最具代表性的是FCM方法.给定一个数据集：X={x1,x2,…,xN},xi∈Rl,1≤i≤N.其中，N为数据集中特征向量总数，l为特征向量维数.定义目标函数为：

(1)

FCM算法通过最小化公式(1)，将数据集X划分到C个模糊簇.在目标函数最小化过程中，隶属度和聚类中心的更新方式为

(2)

FCM方法通过引入模糊权重指数，实现对象的模糊分类，几何意义直观且运算效率高.但该方法对隶属度的约束较为严格，导致算法对噪声较为敏感.

为降低噪声影响，PCM方法放宽了隶属度约束条件，修正后的目标函数为：

(3)

通过放宽隶属度约束条件，PCM方法可以降低噪声对聚类的不利影响.然而，PCM算法对初始凝聚点比较敏感，而且聚类原型可能趋同.

IPCM方法将FCM和PCM方法相结合，得到新的目标函数，为

(4)

IPCM可以有效处理数据重叠和噪声干扰问题.但在处理球状类型的簇时，IPCM方法的运算效率下降严重，而且难以处理复杂的数据结构.

2 CIPCM方法

针对IPCM方法运算效率低和难以处理复杂数据结构的问题，本文提出一种约束IPCM的方法，即CIPCM方法.CIPCM算法采用多项式核将特征向量映射到一个隐性特征空间，便于处理复杂的数据结构；引入必须相连和不可相连两个成对约束集合，提高运算效率和抗干扰能力.该方法的目标函数可以表示为：

(5)

其中，S1是指必须相连约束集合，S2是指不可相连约束集合，约束结合的生成方法见表1.

(6)

公式(5)中，第一项为向量到聚类中心的球面距离的累加和，第二项用于增大典型度，避免噪声干扰，第三项控制违反成对约束的花费，用于提高运算效率和抗干扰能力.

CIPCM方法的实现流程如图1所示.对于输入的数据集X={x1,x2,…,xN}、聚类数量C、核κ={κ1,κ2,…,κM}、每一次迭代的约束条件数量λ、总约束条件数量λtotal和噪声阈值θ，经过自适应迭代过程，输出模糊隶属度矩阵U=[uci]，作为聚类结果.其中，成对约束集合的构建思路是：

函数G(G,U(t),T(t),C,θ,λ)用于生成成对约束集合，伪代码见表1.

图1中，T、U、w和α的更新方式为：

表1 成对约束集合生成算法伪代码

Tab.1Pseudocodefrompairwiseconstrainedset

输入:X,U,T,C,θ,λ输出:S1、S2过程:1.初始化:S(0)1=Ø、S(2)2=Ø;2.估计噪声:Xtci={xi∈X:max(xi)≥θ,∀c=1,2,…,C};3.forc=1:C4.Fc={xi∈Xtci≥θ:Uci≥Uc'i,∀1≤c'≤C,c'≠c}5.endfor6.forc=1:C7.O(Fc,Fc')=∑xi∈FcUFc'min(uci,uc'i)2∑xi∈FcUFc'min(uci,uc'i)8.O(Fc)=1C-1∑Cc'=1,c'≠cO(Fc,Fc')9.endfor10.检测重叠簇:Fm=argmaxFc,c=1,2,…,CO(Fc)11.forc=1:C且c≠m12.qc=λO(Fc,Fm)∑Cc'=1,c'≠cO(Fc,Fm)13.endfor14.forc=1:C且c≠m15.xm=argmaxxj∈Fmumj16.xc=argmaxxj∈Fcucj17.A=Ø18.fori=1:qc19.xa=argmaxxj∈Fm∪Fc,xj∉Amin(umj,ucj)20.A=A∪xa21.查询(xa,xm)的链接表lableam22.iflableam为必连23.S1=S1∪(xa,xm)24.else25.S2=S2∪(xa,xm)26.endif27.查询(xa,xc)的链接表lableac28.iflableac为必连29.S1=S1∪(xa,xc)30.else31.S2=S2∪(xa,xc)32.endif

(7)

其中，

(8)

(9)

(10)

(11)

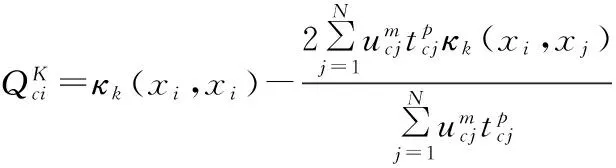
(12)

κk(xi,xj)=φk(xi)Tφk(xj)

(13)

其中，φk(x)为映射核，其与ψk(x)的关系为

(14)

每一个ψk(x)都可以将一个向量x转换为一个L维的向量，这样保证特征空间的所有映射具有相同的维数.通过映射可以形成一个新的正交基，表示为：

(15)

基核采用简单的多项式核，表示为

κk(xi,xj)=(xiTxj+c)k

(16)

3 仿真试验与分析

3.1 试验数据库和评价指标

选用聚类方法评价常用的UCI公共数据集[8]中的4组典型数据库来评测CIPCM方法的性能，实验数据集信息见表2.

图1 CIPCM方法实现流程Fig.1 CIPCM method implementation process

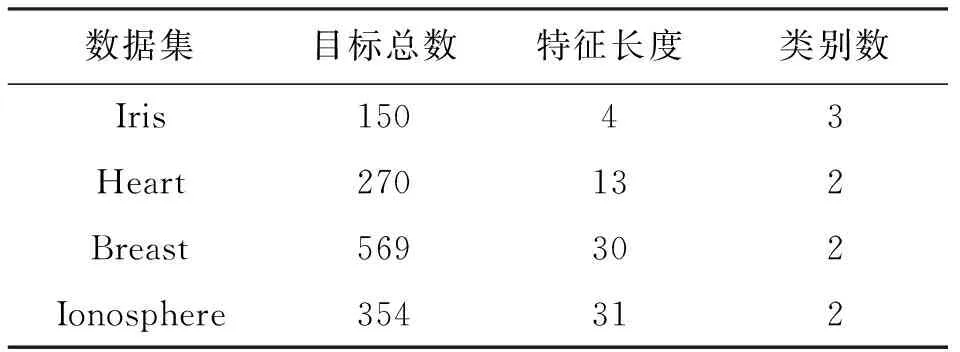
表2 试验数据集信息Tab.2 Information of data set

另外，为了测试算法对噪声的鲁棒性，还对Iris数据集进行加噪处理.文献[9]中对Iris数据集中每一维特征数据上加入0.0～10.0的随机数作为噪声，以便测试算法的鲁棒性.

评价指标采用常用的错分率(MCR)指标，表示为：

(17)

3.2 参数选取

本文方法相关参数的取值见表3.

聚类数量C与数据集中的类别数一致.

表3 相关参数取值Tab.3 The relative parameters

3.3 试验结果与分析

为评价CIPCM方法的性能，将CIPCM方法与FCM[4]、PCM[5]、IPCM[6]以及刘兵等[8]提出的样本加权可能性模糊聚类(sample-weighted possibilistic fuzzy clustering，SWPFC)方法进行对比测试.图2-5给出了不同数据集下的错分率指标.

从图2-5中可以明显看出，CIPCM方法在4个测试数据集下的错分率指标都是最低的，可见本方法优于其他4种方法.

为评价CIPCM方法对噪声的鲁棒性，图6对比了不同方法在加噪Iris数据集下的错分率指标.由图6可见，加噪后CIPCM方法的错分率指标基本不变，说明CIPCM方法对噪声的鲁棒性较强.

图7给出了不同方法在各测试数据集下分类一个目标的平均时间花费对比，单位为毫秒(ms).其中，实验所用的计算机平台为：AMD A6 3.6G CPU、8G RAM、Windows 7.由图7可见，CIPCM方法的处理速度与SWPFC方法相当，比IPCM方法快.尽管比FCM和PCM方法慢，但错分率指标要远高于这两种方法.综合评价认为CIPCM方法的性能较优.

图2 Iris数据集下不同方法的错分率指标Fig.2 Error rate of different methods under Iris data set

图3 Heart数据集下不同方法的错分率指标Fig.3 Error rate of different methods under Heart data set

图4 Breast数据集下不同方法的错分率指标Fig.4 Error rate of different methods underBreast data set

图5 Ionosphere数据集下不同方法的错分率指标Fig.5 Error rate of different methods under Ionosphere data set

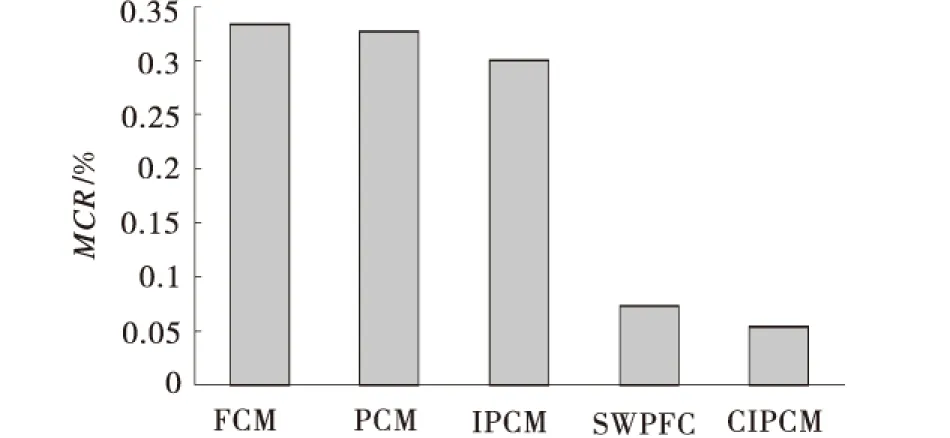
图6 加噪Iris数据集下不同方法的错分率指标Fig.6 Error rate of different methods under the Iris data set

图7 不同方法的时间花费对比Fig.7 Time spent on different methods

4 讨论与结论

针对FCM方法对噪声比较敏感，PCM算法对初始凝聚点比较敏感且聚类原型可能趋同，IPCM方法运算效率低和难以处理复杂数据结构的问题，提出了一种CIPCM方法.通过在国际通用的UCI公共测试数据集上进行性能对比，证明本文方法的错分率指标高于其他方法，且对噪声的鲁棒性更强；同时，新方法的运算效率高于IPCM方法，但仍有待继续提高.另外，相关参数的自适应学习也是下一步研究的方向.

[1] 孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61

[2] 张敏,于剑.基于划分的模糊聚类算法[J].软件学报,2004,15(6):858-868

[3] 张运楚,梁自泽,李恩,等.基于C-均值聚类的视觉监控背景图像构建算法[J].计算机工程与应用,2006,42(14):45-47

[4] Bezdek J C,Ehrlich R.FCM:The fuzzy c-means clustering algorithm[J].Computers & Geosciences,2014(84):191-203

[5] Krishnapuram R,Keller J M.The possibilistic C-means algorithm:insights and recommendations[J].IEEE Transactions on Fuzzy Systems,2009,4(3):385 - 393

[6] Zhang J S,Leung Y W.Improved possibilistic C-means clustering algorithms[J].Fuzzy Systems IEEE Transactions,2004,12(2):209 - 217

[7] 朱婵,许龙飞.聚类算法在基因表达数据分析中的应用[J].华侨大学学报：自然科学版,2005,26(1):7-10

[8] http://archive.ics.uci.edu/ml/[DB/OL]

[9] 刘兵,夏士雄,周勇,等.基于样本加权的可能性模糊聚类算法[J].电子学报,2012,40(2):371-375

[10] 胡靖,张廷伟,刘长仲,等.基于模糊聚类法的亚洲小车蝗种群空间格局分析[J].甘肃农业大学学报,2012,47(3):62-66

(责任编辑 胡文忠)

A constrained improved possibilistic C-means clustering method

XIAO Zhen-qiu1，ZENG Wen-hua2

(1.Computer Academy,Jiaying University,Meizhou 514015,China；2.College of Software,Xiamen University,Xiamen 361005,China)

【Objective】 To solve the problem that improved possibilistic C-means method has low computational efficiency and is hard to deal with complex data structures.【Method】 A constrained improved possibilistic C-means method was proposed.The new method used polynomial kernel to map the feature vector to an implicit space,in order to easily deal with complex data structures and introduced two pairwise constrain set to reduce the number of iteration in the process of data clustering to improve the computational efficiency and anti-interference ability.【Result】 The experiment was implemented on a well-known public testing dataset called UCI,and used misclassification rate to evaluate the performance of object classification.The results showed that the new method had low misclassification rate and strong robustness to noise.【Conclusion】 The computational efficiency of the new method is higher than that of the improved possibilistic C-means clustering method.

clustering;C-means;fuzzy C-means;possibilistic C-means;improved possibilistic C-means

肖振球(1980-)，男， 讲师，硕士，研究方向为计算机应用技术.E-mail:850246398@qq.com

国家自然科学基金面上项目(41172028 )； 国家自然科学基金青年科学基金项目(61403164 ).

2016-03-28；

2016-09-21

TP 391

A

1003-4315(2016)06-0149-06