电火花线切割加工工件厚度在线识别技术研究

李 强，白基成，凡银生

（哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001）

电火花线切割加工工件厚度在线识别技术研究

李 强，白基成，凡银生

（哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001）

通过理论分析方法推导得到工件厚度与放电间隙两端间的平均电压、平均电流、机床伺服进给速度、线切割缝宽等参数的关系式。采用田口试验方法分析不同加工参数下电火花线切割加工不同厚度工件时放电两极之间平均电压、平均电流、线切割缝宽及加工速度的影响规律，研究一种基于灰色理论的线切割缝宽预测模型，并基于该模型研究一种基于广义回归模型在线识别电火花线切割加工工件厚度的方法。工件厚度在线识别技术可实现电火花线切割加工时对工件厚度的预测，是电火花线切割自适应加工变厚度工件的前提和关键。

电火花线切割加工；工件厚度；在线识别；灰色理论；非线性回归

电火花线切割加工因具有无残余应力、加工效率较高等优势而被广泛应用于模具工业及航空航天等领域[1]。电火花线切割加工的工件包含阶梯孔、楔形台、圆、椭圆等不同的结构形貌，在加工过程中工件厚度随着加工的进行会发生连续变化或突变。实验证明，在不改变加工参数的情况下，随着工件厚度的减小，伺服加工速度会逐渐变快，导致放电集中，且易发生断丝现象；反之，工件厚度增大，伺服加工速度会逐渐变慢，导致加工效率降低。因此，当加工过程中工件厚度发生变化时，如何使机床伺服进给速度随工件厚度的变化保持在一个理想的范围，是保证电火花线切割加工精度和加工效率的重要前提，而在线识别工件厚度是该问题的关键。

近年来，各国学者对线切割加工工件厚度的识别技术做了大量研究。廖运炫等针对等能量脉冲电源，利用蚀除材料体积与放电能量之比的比放电能概念，建立了一个工件厚度、加工速度与放电频率之间的数学模型，实验证明该模型适用于预测工件厚度变化不大的电火花线切割加工[2-3]。豆尚呈等选择放电频率、进给速度、伺服电压和脉冲间隔作为输入量，建立了工件厚度辨识的支持向量回归机模型，能较准确地预测工件厚度[4]。目前针对线切割厚度识别技术的研究主要存在于单向走丝电火花线切割机床中，且工件厚度识别主要是利用等能量脉冲电源在电火花线切割加工时的放电频率、脉冲间隔、进给速度等影响因素来建立预测模型，实现工件厚度的预测[5]。但这些模型都是建立在线切割缝宽不变的情况下，而在实际加工过程中，不同的加工参数产生的线切割缝宽是变化的；同时，脉冲电源的类型也不仅仅只有等能量脉冲电源一种，这就造成了目前变厚度识别技术的局限性。

本文针对往复走丝电火花线切割机床的变厚度加工问题，基于不同参数加工不同厚度工件时两极之间的平均电压、平均电流和伺服速度，提出了一种基于灰色理论的线切割缝宽预测方法和一种基于广义回归模型在线识别工件厚度的方法。实现工件厚度的在线识别，对进一步研究自适应电火花线切割加工、促进电火花线切割加工技术的发展具有重要意义。

1 工件厚度在线识别技术的理论分析

虽然往复走丝电火花线切割加工原理和单向走丝电火花线切割加工原理并无二致，但由于走丝机构、工作液、电极丝、脉冲电源等方面的差异，使得在往复走丝电火花线切割加工变厚度工件过程中，影响线切割加工稳定性和加工效率的参数会较多，放电过程也会更复杂，因此选择哪些加工参数来研究工件厚度辨识因素尤为重要。

在电火花线切割加工中，工件和电极丝之间形成放电通道，通道中的电子和正离子受电场作用分别向正、负极快速移动，并发生剧烈碰撞，脉冲电源提供的电能被转换为热能、蚀除材料的动能、光能等各种能量[1]。根据放电能量公式，在一定的加工时间内，放电能量可表示为：

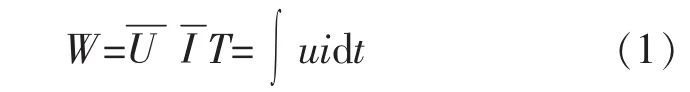
式中：T为加工时间；U、I分别为加工过程中放电两极之间的平均电压和平均电流；u、i分别为加工过程中放电两极之间的瞬时电压和瞬时电流。

在电火花线切割加工过程中，放电两极之间消耗的能量即脉冲电源在放电两极之间产生的放电能量一般可分成三部分：一部分用于工件材料的蚀除，一部分作用于电极丝上，其余部分以热能、光能的形式扩散到工作液中。放电总能量W的能量分配关系可表示为：

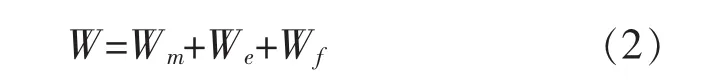
式中：Wm为蚀除工件材料消耗的能量；We为电极丝上消耗的能量；Wf为扩散至工作液中的能量。

从目前各国学者对电火花加工时工件和电极之间的放电能量分配问题所做的试验研究成果可得出：利用不同的工件、电极材料，在不同的电火花加工环境中进行电火花加工实验，正、负极两端的能量分配系数α是不一样的，且能量分配系数与工作液、电加工参数、工件和电极材料等因素有着非常密切的联系[6-8]。但在电火花线切割加工时，影响能量分配系数的各种加工参数在设定后一般是不会改变的，即可认定α在这种情况下也是不变的，且蚀除的工件材料体积与加工过程中的放电能量成正比。

本文利用往复走丝电火花线切割机床开展工件厚度在线识别技术的研究，在加工过程中，线切割加工的环境、工作液、工件和电极材料均一致，那么能量分配系数仅与线切割机床的可变加工参数有关。有效放电能量Wm可表示为：

式中：α为放电能量作用于工件材料蚀除部分的能量分配系数。

有效放电能量主要体现在工件材料熔融的热能和抛出时的动能，定义电火花加工中蚀除单位体积的有效放电能量为比放电能 （specific discharge energy，Wo），可表示为：

式中：V为工件材料蚀除的体积。

电火花线切割加工工件的截面示意图见图1，则工件材料蚀除的体积可表示为：

式中：H为工件厚度；B为线切割缝宽；S为机床进给伺服加工速度；T为加工时间。

图1 电火花线切割加工缝宽示意图

由图1可知，线切割缝宽B主要由放电间隙G和电极丝直径d的大小决定，可表示为：

放电间隙是电火花线切割加工过程中工具电极与工件之间的距离，一般来说其大小在加工过程中是变化的，直接影响加工精度和加工效率。放电间隙可用经验公式表示为：

式中：Ku为与工作液介电强度有关的常数；ûi为开路电压；KR为常数，与加工材料有关，一般易熔金属的值较大；WM为单个脉冲能量；Sm为考虑膨胀、收缩、振动等影响的机械间隙。

那么，电火花线切割加工缝宽B即可表示为：

从式（9）可看出，工件厚度的预测与单位时间内的平均电压、平均电流、线切割缝宽、机床伺服进给速度、能量分配系数等都有着密切联系。在电火花线切割加工过程中，平均电压、平均电流、机床伺服进给速度均较易通过外部检测电路及数据采集卡实时采集得到，但线切割加工缝宽则无法实时在线获取，因此本文在建立工件厚度预测模型之前就应建立一个线切割缝宽的预测模型。由前文分析可知，能量分配系数、放电间隙等与电火花线切割加工参数有很大关系，在综合考虑往复走丝电火花线切割加工机床特性及当前可改变条件的基础上，选择对加工质量、加工效率影响较大的加工参数（如脉宽、占空比、峰值电流、电极丝丝速）作为本文研究工件厚度在线识别技术的输入量。

通过式（8）可知，在工作液、开路电压、工件材料、加工外部环境一定的条件下，线切割缝宽仅与单个脉冲能量有关，即与电火花加工过程中选择的电加工参数有关。

综合式（1）～式（5）整理得到工件厚度H的表达式为：

2 实验条件和方法

针对往复走丝电火花线切割加工的工件厚度在线识别技术的研究，利用DK7732往复走丝电火花线切割机床，对机床电路进行改进以达到实验要求，改进后的实验装置见图2。

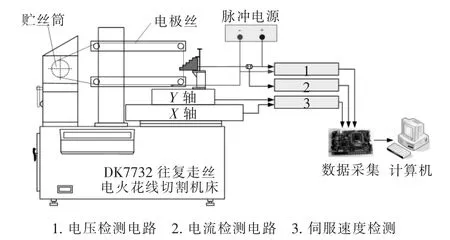
图2 电火花线切割加工实验装置示意图

为了能有效、实时检测放电两极之间的平均电压、平均电流和机床伺服进给速度，并提高采样精度，采用采样频率500 Hz、采集范围0～10 V、采样精度0.001 V的8通道模拟采集卡对电压、电流、机床伺服进给速度信号进行实时采集，并将信号通过USB2.0接口传送至计算机中，以便进行后续的数据处理。

电压检测电路将放电两极之间的放电电压信号进行滤波、分压、隔离等操作，然后将压降后的电压信号直接输出至采集卡。电流检测电路采用采样频率为150 kHz的电流传感器CSNP661t作为脉冲电源主回路电流的检测元件，将电流信号转化成电压信号，然后经滤波、隔离等操作输出至采集卡。伺服进给速度检测电路从X、Y轴的步进电机驱动信号入手，对数控系统输出的驱动信号进行采样，并进行后续处理输出至采集卡。同时，由于往复走丝电火花线切割机床在加工过程中有一个周期性的电极丝换向过程，在此期间脉冲电源会切断能量的供给，机床也会停止伺服进给运动，因此通过采集换向开关的换向信号，对换向期间的电压、电流、伺服速度信号不做接收和后续处理。

此外，利用DK7732往复走丝电火花线切割机床进行实验研究的其他条件如下：电极丝为直径0.18 mm的钼丝，工作液介质为JR3A复合工作液，工件材料为Cr12MoV模具钢，开路电压为100 V。

3 实验设计和结果

本文选择脉宽、占空比、峰值电流及电极丝丝速等加工参数作为影响因素，每个参数选择5个不同的水平。由于所选加工因素较多，且各因素之间具有一定的关联性，若对所有参数组合进行实验，会使数据量太大，所以本文以平均电压、平均电流、伺服加工速度、线切割缝宽为研究目标，采用田口试验方法[9]进行电火花线切割变厚度实验设计，以减小工作量。由于平均电压、平均电流、伺服加工速度能通过实验装置直接得到，而线切割缝宽到目前为止并没有特别合适的在线测量方法，因此本文利用超景深显微镜对加工后的工件进行放大处理，再进行线切割缝宽的测量（图3）。利用Minitab软件进行田口试验设计，每组实验均进行3次，对所得数据结果求取平均值，实验设计及其结果见表1。

图3 利用超景深显微镜测量线切割缝宽示意图

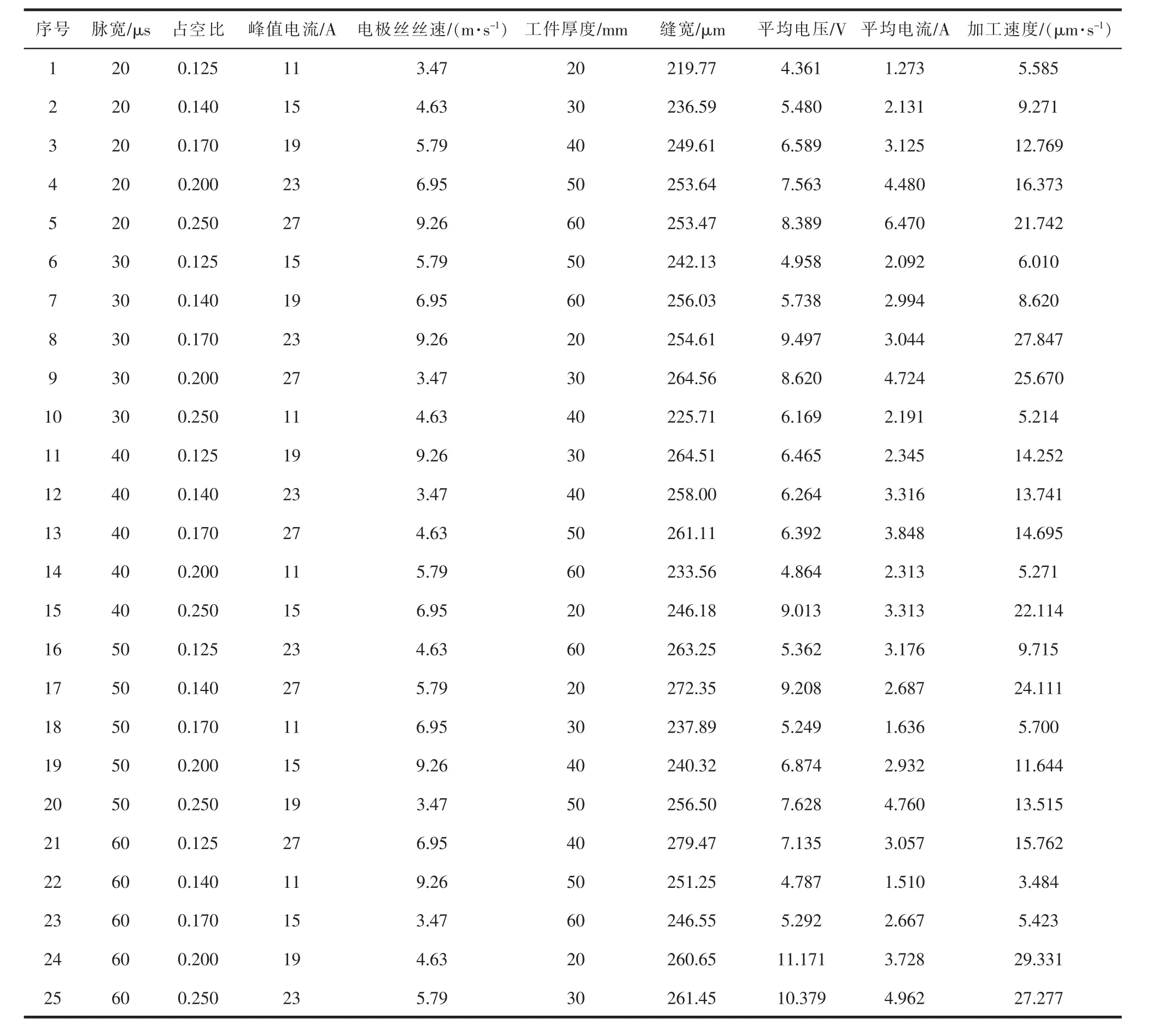
表1 实验设计及结果

4 线切割缝宽预测模型的研究

通过工件厚度在线识别的理论分析可知，要建立工件厚度预测模型进而实现工件厚度在线预测，首先就要明确线切割缝宽的大小，而目前很难对其进行在线测量，因此本节主要建立线切割缝宽的预测模型，从而实现线切割缝宽的实时预测。

灰色系统（Gray system）理论和方法是近年来广泛应用的一种预测算法，是一种研究少数据、贫信息、不确定性问题的新方法[10]。其关联度分析方法是灰色系统分析、预测、决策的基础，可为因素判别、优势分析和预测精度检验等提供依据。灰色系统建模是以灰色过程概念为基础，通过关联度分析，理清系统中各因素间的主要关系，找出影响最大的因素。最后将模型预测值作一次累减还原，用以对系统进行预测。由于在电火花线切割加工中影响线切割缝宽的因素较多，无法一一分析，还有很多不确定因素，且实验数据有限，可认为信息不完全，而不确定因素是灰色因素，符合灰色系统的研究条件。因此，本文采用灰色系统理论方法建立线切割缝宽与脉宽、占空比、峰值电流、电极丝丝速的预测模型，实时预测电火花线切割加工时的线切割缝宽。

经典GM（1，N）模型是灰色系统模型中最常见的模型之一，对应于一阶微分方程，进行一次累加，变量数为N。研究发现，经典GM（1，N）模型具有二个缺陷：一是假定了相关因素间的线性关系；二是当参数列求出后，进一步求解较难。针对该问题，提出2种不同形式的非线性优化GM（1，N）模型——GM（1，N，x1（0））模型和GM（1，N，x1（1））模型，能实现非线性的预测。2种非线性模型的不同之处在于以原始值还是累加值作为目标值，在具体运用中可根据预测精度有比较性地选取，或根据预测数据的增长情况或波动情况选取。当数据增长较慢时，一般选择非线性GM（1，N，x1（0））模型；而当数据增长相对较快或数据波动频繁时，为了充分降低数据的波动性和灰性，一般选取非线性GM（1，N，x1（1））模型[11]。 众所周知，线切割缝宽与脉宽、占空比、峰值电流、电极丝丝速之间的关系式为非线性的，且数据波动较大，综合考虑上述因素，选择非线性GM（1，N，x（1））

1模型作为本文线切割缝宽的预测模型。

为了计算简便，设定线切割缝宽为x1，脉宽为x2，占空比为x3，峰值电流为x4，电极丝丝速为x5。将表1所示实验数据初值化，结果见表2。

表2 实验数据初值化

对初值数据进行一次累加，结果见表3，得到的向量矩阵为：

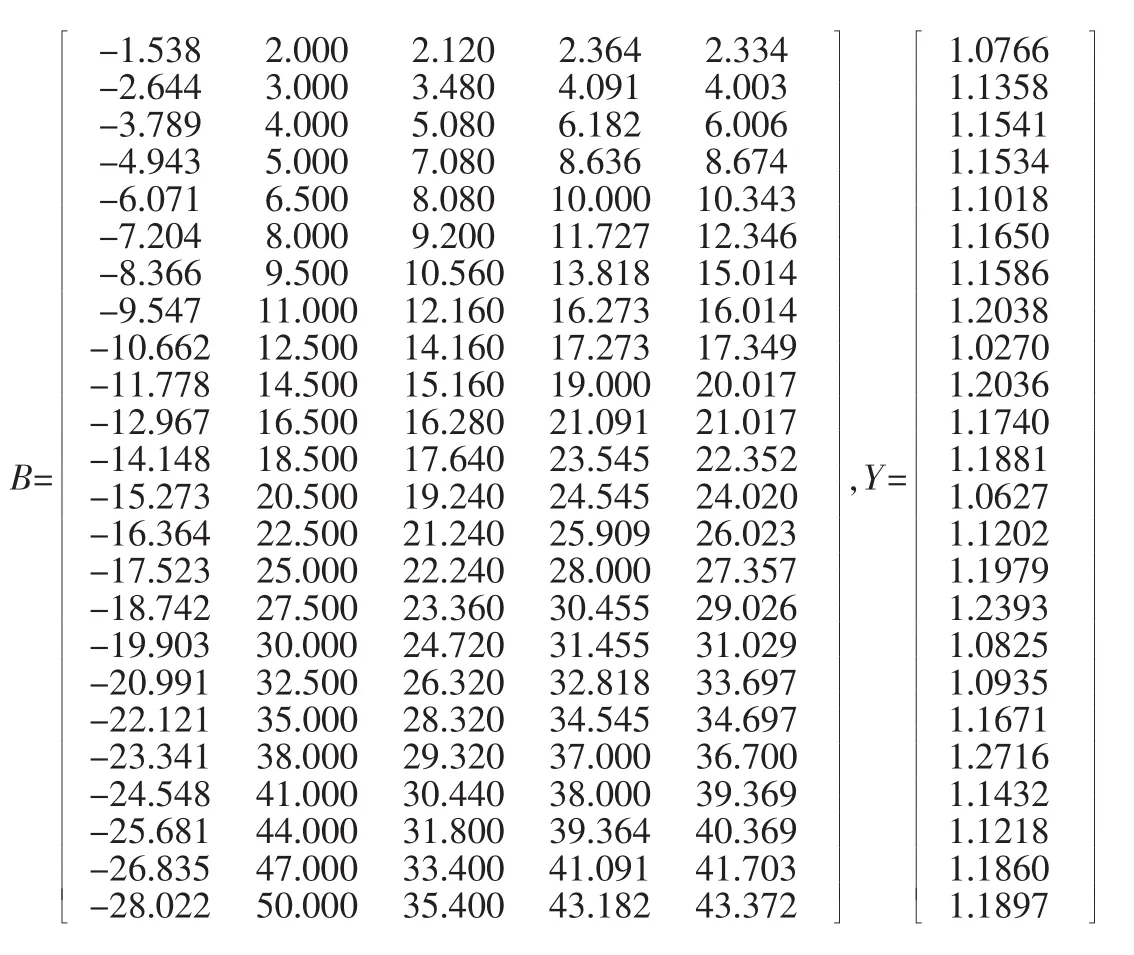
B=■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■-1.538 2.000 2.120 2.364 2.334 -2.644 3.000 3.480 4.091 4.003 -3.789 4.000 5.080 6.182 6.006 -4.943 5.000 7.080 8.636 8.674 -6.071 6.500 8.080 10.000 10.343 -7.204 8.000 9.200 11.727 12.346 -8.366 9.500 10.560 13.818 15.014 -9.547 11.000 12.160 16.273 16.014 -10.662 12.500 14.160 17.273 17.349 -11.778 14.500 15.160 19.000 20.017 -12.967 16.500 16.280 21.091 21.017 -14.148 18.500 17.640 23.545 22.352 -15.273 20.500 19.240 24.545 24.020 -16.364 22.500 21.240 25.909 26.023 -17.523 25.000 22.240 28.000 27.357 -18.742 27.500 23.360 30.455 29.026 -19.903 30.000 24.720 31.455 31.029 -20.991 32.500 26.320 32.818 33.697 -22.121 35.000 28.320 34.545 34.697 -23.341 38.000 29.320 37.000 36.700 -24.548 41.000 30.440 38.000 39.369 -25.681 44.000 31.800 39.364 40.369 -26.835 47.000 33.400 41.091 41.703 -28.022 50.000 35.400 43.182 43.372■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■，Y=■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■1.0766 1.1358 1.1541 1.1534 1.1018 1.1650 1.1586 1.2038 1.0270 1.2036 1.1740 1.1881 1.0627 1.1202 1.1979 1.2393 1.0825 1.0935 1.1671 1.2716 1.1432 1.1218 1.1860 1.1897■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■

表3 初值数据一次累加值

因为n=25、N=5，所以n＞N+1，在最小二乘准则下，由â=（BTB）-1BTY，可求参数a及b。利用Matlab软件和上述计算方式可得：a=0.5444，b2=-0.0787，b3=0.3740，b4=0.0446，b5=0.1184。

根据GM（1，N）的白化微分方程[11]：

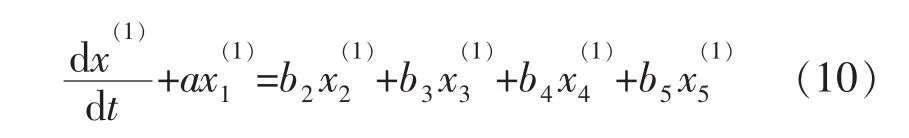
可表示为：

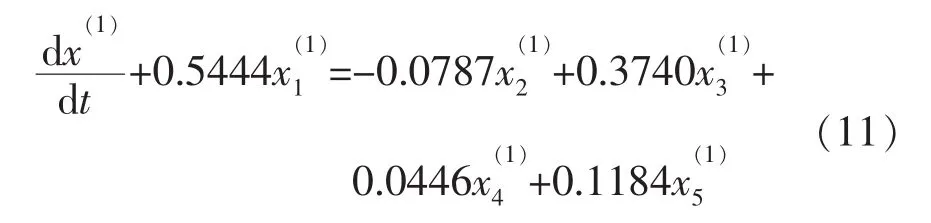
进一步，GM（1，N，x（1）1）模型

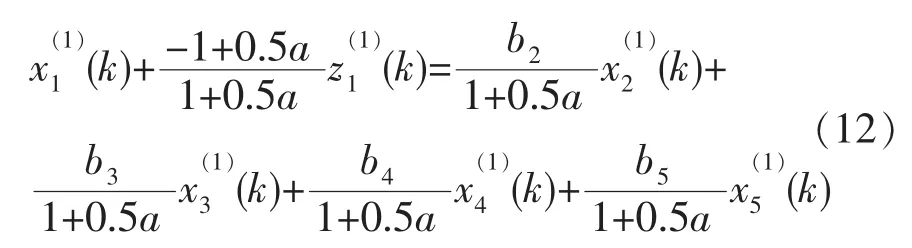
可表示为：

结合表3，通过计算得到的线切割缝宽预测模型为：

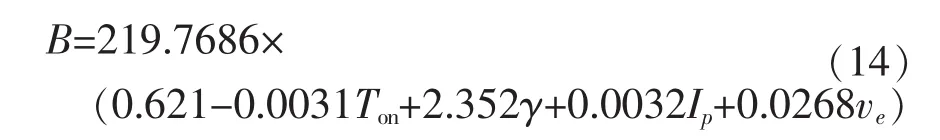
式中：Ton为脉冲宽度；γ为占空比；Ip为峰值电流；ve为电极丝丝速。

利用灰色理论建立线切割缝宽的预测模型，可在已知电加工参数的情况下准确预测出线切割加工的缝宽大小，为工件厚度在线识别模型的建立提供了基础数据。

5 工件厚度预测模型的研究

根据式（9）的分析可知，在明确了电火花线切割加工的平均电流、平均电压、线切割缝宽及机床伺服进给速度后，只需通过非线性拟合方式得到能量分配系数中的其他未知参数，就能建立工件厚度预测模型。因此，式（9）可转变为：

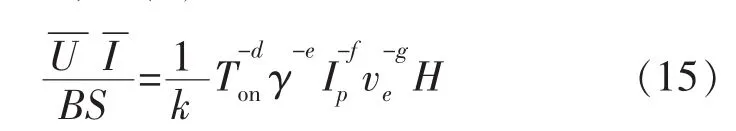
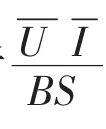
6 工件厚度预测模型的验证实验

为了验证线切割缝宽预测模型、工件厚度预测模型的正确性以及在线识别技术的可行性，本文利用往复走丝电火花线切割机床进行了梯形工件的加工实验。实验装置和加工条件不变，可变加工参数分别为：脉宽45 μs，占空比0.14，峰值电流23 A，电极丝丝速6.95 m/s。为了能顺利测出线切割缝宽，对最后一个阶梯进行不完全加工，即保留一部分，使工件不被切断。梯形工件示意图见图4。用超景深显微镜每隔1.5 mm左右测量一次实际线切割缝宽，可得到缝宽的实际变化趋势。

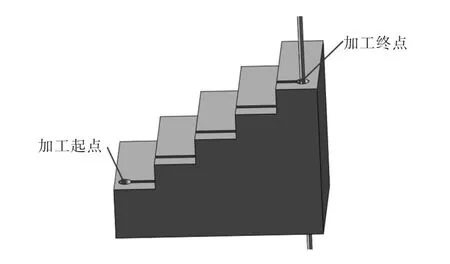
图4 梯形工件加工示意图

将验证实验所用的加工参数代入线切割缝宽预测模型，由式（14）计算得到线切割缝宽预测值为235.29 μm。将该预测值和真实值进行对比，可看出，真实值在一个较小的范围内波动，真实值的平均值为237 μm，和预测值相差极小（图5）。由此可认为线切割缝宽预测模型基本正确，该模型能非常准确地预测线切割缝宽的数值大小，为进一步预测工件厚度提供了可靠的数据。

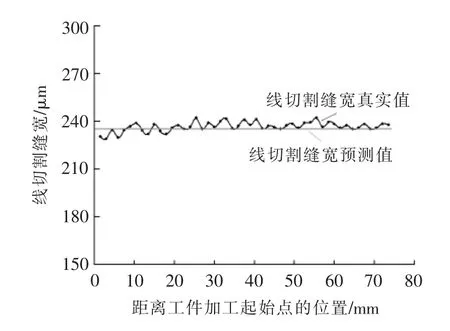
图5 线切割缝宽真实测量值和预测值的对比

在线切割缝宽预测值的基础上，结合电火花线切割加工验证实验采集到的平均电流、平均电压及机床伺服进给速度等数据，代入工件厚度预测模型。由式（16）可计算得到电火花线切割各加工时刻的工件厚度预测值，将其与真实值进行比较，结果见图6。可看出，预测模型得到的工件厚度与实际工件厚度基本一致，且工件厚度预测值均在真实值上下浮动，波动范围较小，能满足电火花线切割加工不同厚度工件的辨识度要求。同时，导致工件厚度预测值与真实值之间存在差距的原因，主要在于往复走丝电火花线切割加工时两极之间的放电较复杂，加工过程中工作液等其他因素会有一定的改变，尤其是在正、反转的换向起始、结束阶段。因此，从整体上看，验证实验证实了电火花线切割工件厚度预测模型的正确性，能较准确地预测工件厚度。

图6 工件厚度预测值与真实值对比图

7 结论

（1）从理论上分析了往复走丝电火花线切割加工中影响工件厚度识别的因素主要有：能量分配系数、线切割缝宽、平均电压、平均电流、机床伺服进给速度等。选取脉宽、占空比、峰值电流、电极丝丝速等加工参数作为研究对象，利用Minitab软件进行了田口试验设计，并获得了电火花线切割在不同加工参数下加工不同厚度工件的平均电压、平均电流、线切割缝宽、伺服加工速度等数据结果。

（2）采用灰色系统理论方法建立一个线切割缝宽预测模型，主要用于预测不同加工参数时的线切割缝宽大小。采用多元非线性回归方法，用Matlab软件的非线性函数计算并建立了一个工件厚度在线识别模型，利用该模型能实时预测不同加工参数时往复走丝电火花线切割加工工件的当前厚度。

（3）进行了往复走丝电火花线切割加工梯形工件的验证实验，证明本文建立的线切割缝宽预测模型及工件厚度在线识别模型的正确性，工件厚度在线识别技术能较准确地辨识工件厚度，为提高变厚度工件的加工精度提供了关键数据。

[1] 白基成，刘晋春，郭永丰.特种加工[M].6版.北京：机械工业出版社，2014.

[2] LIAO Y S，CHUANG T J，YU Y P.On-line workpiece height estimation and its application in servo feed control of WEDM process[J].Procedia CIRP，2013，6：226-231.

[3] LIAO Y S，YAN M T，CHANG C C.A neural network approach for the on-line estimation of workpiece height in WEDM[J].Journal of Materials Processing Technology，2002，121（2-3）：252-258.

[4] 豆尚成.变厚度电火花线切割加工过程控制系统[D].上海：上海交通大学，2013.

[5] 宗福来.电火花线切割变厚度加工自适应控制技术的研究[D].哈尔滨：哈尔滨工业大学，2006.

[6] ZAHIRUDDIN M，KUNIEDA M.Energy distribution ratio into micro EDM electrodes[J].Journal of Advanced Mechanical Design Systems and Manufacturing，2010，4（6）：1095-1106.

[7] SINGH H.Experimental study of distribution of energy during EDM process for utilization in thermal models[J]. International Journal of Heat and Mass Transfer，2012，55（19）：5053-5064.

[8] 高睿恒，张发旺，顾琳，等.水中电火花放电能量分配系数研究[J].电加工与模具，2014（2）：1-4.

[9] MAHAPATRA S S，PATNAIK A.Optimization of wire electrical discharge machining (WEDM) process parameters using taguchi method[J].The International Journal of Advanced Manufacturing Technology，2007，34（9-10）：911-925.

[10]刘思峰，杨英杰，吴利丰.灰色系统理论及其应用[M].7版.北京：科学出版社，2014.

[11]周伟，方志耕.非线性优化GM（1，N）模型及其应用研究[J].系统工程与电子技术，2010，32（2）：317-320.

Study on Online Identification Technology of Workpiece Height in WEDM

Li Qiang，Bai Jicheng，Fan Yinsheng
（School of Mechatronics and Engineering，Harbin Institute of Technology，Harbin 150001，China）

This paper derived the relationship expression between workpiece height and average voltage,average current，servo feed rate of wire electrode，the process width with theoretical analysis method.A taguchi experiment was adopted to found the effect laws of different processing parameters and different heights workpiece.A predicting model on the process width was built based on grey theory.By this predicting model，a mathematical model based on multi-nonlinear regression method was built.The online identification technology of workpiece height could predict workpiece height online in different process parameters，which was the key point of adoptive process control for variable workpiece height in wire electrical-discharge machining(WEDM).

WEDM；workpiece height；online identification；grey theory；nonlinear regression

TG661

A

1009－279X（2016）06－0029-07

2016-06-22

国家自然科学基金资助项目 （51575137，51175120）；哈尔滨市应用技术研究与开发项目（2015RAXXJ027）

李强，男，1987年生，博士研究生。