双任务协调、任务呈现方式影响成人算术策略执行：估算证据*

2016-02-02

心理学报 2016年6期

(山东师范大学心理学院,济南 250358)

1 前言

1.1 当前策略执行机制的理论探索

前人研究显示,为更好解决特定问题,在面对不同任务乃至同一任务时,个体会倾向于运用不同策略(Lemaire,Lecacheur,&Farioli,2000;Siegler,2007;司继伟,杨佳,贾国敬,周超,2012等)。策略运用被看作个体认知加工的关键环节。认知策略的运用主要包括策略选择和策略执行两个主要环节(Siegler&Lemaire,1997)。策略选择指个体根据给定的任务或环境,合理选择策略,有效解决问题,即如何选择策略来解决已知问题(Mata,Josef,&Lemaire,2015)。而策略执行指个体使用某种策略解决问题的速度和准确性,即在适当的时间,以合适的顺序,正确执行所有步骤的能力(Mata et al.,2015)。人们不仅可以考察策略执行效能(Imbo&LeFevre,2009),也可考察某一具体策略的内部加工过程,及个体有效执行策略的能力。由于策略执行较策略选择简单,且可反映策略本身的特性(速度和准确性),因此成为考察个体认知策略运用特征的一种良好指标。探讨策略执行,有助于深化对认知策略运用机制的认识,验证和丰富已有的策略理论。

当前主要认知策略理论认为策略运用与认知系统(如准确性、时间和努力程度)或环境因素有关。如Shrager等人早期提出的策略的选择及发现模型(Model of Strategy Choice And Discovery Simulation,简称SCADS)强调元认知对策略更新与选择的作用(Shrager&Siegler,1998);在此基础上,

SCADS

修正模型增加了注意控制的作用(Siegler&Araya,2005)。而近年发展起来的策略选择学习理论(Strategy Selection Learning theory,简称SSL)强调人们对策略的选择与执行是根据策略解决问题的准确性来调整的(Rieskamp&Otto,2006),而认知龛理论(Cognitive Niches Theory)则认为策略的可用性是认知系统与环境之间的相互作用(Marewski&Schooler,2011;张俊,刘儒德,2011)。

即使上述理论模型的侧重点各有不同,但它均关注一个主要问题——被试究竟如何执行策略(Hinault,Dufau,&Lemaire,2014),即在策略执行中,其内部加工过程受哪些因素影响？不少实证研究已发现策略选择与执行受多种因素的影响,如策略效率(Cepeda,Pashler,Vul,Wixted,&Rohrer,2006;Mata,Schooler,&Rieskamp,2007;Rieskamp&Otto,2006;Roediger&Karpicke,2006)、策略难度(Lemaire,Arnaud,&Lecacheur,2004;Lemaire&Lecacheur,2010;Torbeyns,Verschaffel,&Ghesquière,2005;Uittenhove&Lemaire,2012)、任务难度(Benjamin&Bird,2006;Son,2010;Hinault,Dufau,&Lemaire,2014;Toppino,Cohen,Davis,&Moors,2009)、中央执行(Caviola,Mammarella,Cornoldi,&Lucangeli,2012;Imbo,Vandierendonck,&De Rammelaere,2007;王明怡,陈英和,2006)和情景因素(Lemaire&Callies,2009;Leonhard&Ulrich,2011;Hinault et al.,2014;Töllner,Strobach,Schubert,&Müller,2012)等。接下来分别阐述国内外关于策略本身特征、中央执行功能和情景因素是如何影响策略执行的现有发现。

不少证据显示,个体对不同策略的运用易受策略本身具有的特点影响,这种特点指策略选择和执行的速度以及准确性(Hinault et al.,2014)。不同策略具有不同的选择和执行效率。估算研究中常用策略有上调策略和下调策略(司继伟,徐艳丽,封洪敏,许晓华,周超,2014)。上调策略指将每个加数向上调整为与它最接近的整十、整百数(如,48+56上调成为50+60)进行计算;下调策略将每个加数向下调整为与它最接近的整十、整百数(如,将43+54下调成为40+50)。相关研究均发现,下调策略的正确性和反应时均优于上调策略,且与问题难度无关(Uittenhove&Lemaire,2012,2013)。

1.2 双任务协调与策略执行

策略执行可能受到中央执行功能中双任务协调功能的影响。中央执行被认为是工作记忆系统中最为复杂的成分(Baddeley,2012;周仁来,赵鑫,2010)。自上世纪90年代,算术认知领域的研究者逐渐意识到中央执行对个体的算术认知活动有着极其复杂的影响,如策略执行(Bull,Johnston,&Roy,1999;Lemaire&Reder,1999;Navon&Miller,1987;Pashler,1994;Siegler&Lemaire,1997;罗琳琳,周晓林,2004)。中央执行具有可分离性(Miyake et al.,2000;陈天勇,李德明,2005),包括刷新(updating)、抑制(inhibition)、转换(shifting process)以及双任务协调(dual-task coordination)四种功能(Collette&van der Linden,2002),双任务协调是中央执行的重要功能之一(Logie,Cocchini,Della Sala,&Baddeley,2004;Baddeley,1996)。双任务协调指同时处理需不同认知加工的双任务的能力。双任务协调过程消耗任务准备和刺激感知与运动反应加工(Lussier,Gagnon,&Bherer,2012)。相对单任务,双任务的执行力更慢(反应时增加、错误率更高),这种增加的反应时和错误率即为双任务协调代价。

双任务代价相当明显,甚至在任务刺激的输入和反应输出没有冲突的情况下也出现,目前对双任务协调代价的减少机制仍不明朗(Strobach,Frensch,Müller,&Schubert,2012;杨佳,李颖慧,司继伟,张明亮,2011)。无论简单或复杂算术任务,中央执行对其产生巨大作用,中央执行功能(尤其是双任务协调、抑制与刷新功能)对多位数的运算、心算及问题解决存在重要影响(Iuculano,Moro,&Butterworth,2011;Noel,2009;Raghubar,Barnes,&Hecht,2010;Swanson,Jerman,&Zheng,2008)。少量证据显示,双任务协调与儿童不同算术认知的策略选择及执行分别呈现出了一定程度的相关,无论是简单任务还是复杂任务,对中央执行系统的干扰都会造成整体策略执行效果的下降(王明怡,陈英和,2006;陈英和,王明怡,2009)。陈英和与王明怡(2009)采用双任务范式考察儿童算术认知策略如何受到中央执行功能的影响,发现双任务协调与增加策略放弃次数呈负相关。作为中央执行系统的重要成分之一,双任务协调可能会参与到个体的策略运用中(陈英和,王明怡,2009)。而目前探讨双任务协调与算术策略运用之间关系的研究还相对较少。考察双任务协调对个体算术策略运用的影响,有助于完善对中央执行系统在个体策略运用中所扮演角色的认识,结合以往研究,可以清楚地阐释不同中央执行成分在个体策略运用中所发挥作用,及其他们之间的差异性与联系性,从而深入理解中央执行系统在数学认知中的关键作用。

研究双任务协调代价最常见的范式是心理不应期(psychological refractory period,简称PRP)范式,常用来研究双任务加工过程中的影响因素(Pashler,1994;Miller,Ulrich,&Rolke,2009),为微观分析双任务的加工过程提供方法支持。在该范式中,操纵两个任务选择反应时上的重叠,采用耗损的反应时间和准确率评估两个任务。一般的PRP范式设计思想如下：相继呈现刺激S1和S2,两个刺激间采用一定时间间隔(SOA),要求被试迅速对两种刺激做出反应,第一刺激(S1)对应反应一(R1),第二刺激(S2)对应反应二(R2),即S1-S2-R1-R2的顺序(Pashler,1994;Pashler&Johnston,1998),进而探讨两种刺激反应之间的相互干扰。本研究采用PRP双任务范式,同时借鉴分支双任务范式的思想,通过控制任务呈现方式、反应顺序和数量,分别将PRP范式中的S2拆分为S2a和S2b,采用S1-S2a-S2b-R2-R1和S2a-S1-S2b-R2-R1的顺序,考察个体在保持双任务中一个任务加工的同时,如何进行另一任务加工的双任务协调,即如何在对一个任务进行抑制延迟的同时,灵活地进行另一个任务的双任务协调。改变任务呈现方式和任务反应序列逆序(第一种顺序)或中断(第二种顺序),让双任务中其中的一个刺激先进入,并处于工作记忆保持状态,同时需要对另一任务进行加工与操作。在此阶段,既要求我们对先前任务进行工作记忆保持,同时要求对第二任务(估算)操作加工,此阶段为双任务协调阶段,以此考察双任务协调对估算策略运用的影响。Lussier等(2012)的研究中,采用双反应的策略执行效能(RT,ACC)减去对应的单反应的策略执行效能(RT,ACC)衡量双任务协调代价。该计算公式是基于控制了双任务中的反应顺序和反应数量。且其单双任务是按照反应数量区分的,即单任务指双任务单反应,双任务指双任务双反应两种。而并不是单任务只呈现一种任务,而是两种任务都呈现,但要求被试只对其中的两位数加法估算任务反应。如此,两种任务中均存在任务间的转化、刷新和抑制,而双任务协调代价用双反应的执行效能(RT、ACC)减去相应的单反应的执行效能,从而控制了单任务和双任务在转化、刷新和抑制上的差异。本研究借鉴Lussier等人衡量双任务协调代价的思想,探讨了双任务协调对策略执行的影响。

1.3 任务呈现方式与策略执行

双任务情景中存在着任务呈现方式和任务呈现序列两个不同的变量。任务呈现序列是试次内变量,指双任务情景中,主任务和次任务的呈现顺序,即谁先呈现的问题。任务呈现方式是试次间变量,指前后试次任务呈现序列是否相同,包括随机呈现方式和固定呈现方式两种。认知龛理论认为策略运用受认知系统与环境之间相互作用的影响(Marewski&Schooler,2011;张俊,刘儒德,2011),那么任务呈现方式所提供的环境对策略的执行是否有影响？策略运用可能受到任务呈现方式的影响(Lemaire&Callies,2009)。有研究发现,个体在双任务情景中,反应时间延长,错误率升高,两个任务行为均受影响,但是改变任务难度或者调整情景的设置,个体的双任务代价却会降低(Liepelt,Strobach,Frensch,&Schubert,2011)。人们使用PRP范式探讨双任务协调,发现双任务中首先反应的任务主要受到任务呈现方式的影响(Sigman&Dehaene,2006;Töllner et al.,2012)。冲突监测理论认为冲突适应效应主要是由于个体对先前冲突的监测,提高了认知控制及调整,更好地完成当前试次中的任务(Olszanowski,Bajo,&Szmalec,2015;刘培朵,杨文静,田夏,陈安涛,2011)。根据冲突监控理论,在双任务协调情景中,当两个刺激的加工过程是两个不同的任务时,竞争出现在任务间,引起所谓的双任务代价。个体进行双任务后,会激活一种较大的自上而下调整,该调整降低信息加工过程的冲突,使整体反应加快,且在不一致情景下,该自上而下调整更大。因此,任务呈现方式可能影响到策略执行效能(Olszanowski et al.,2015)。Leonhard等(2011)在总结前人研究基础上,曾设计了3个实验(实验1为固定序列方式视听双任务,实验2为随机序列方式视听双任务,实验3为视听双任务与单任务随机方式呈现)探讨在PRP范式中中央加工序列的影响因素(Leonhard&Ulrich,2011)。结果表明,序列的不可预测性影响策略执行的行为效能,即任务呈现方式影响策略执行。Szameitat,Schubert,Müller和von Cramon(2002)为探讨双任务中执行功能间的神经联系,利用fMRI技术和PRP范式,设置固定组(两任务呈现顺序固定)和随机组(随机呈现两任务),发现双任务中下额叶、额中回和顶内沟有激活,且在随机组激活更大。任务呈现方式间的差异有神经基础,两种方式的神经激活程度不同,其策略执行的行为效能是否有差异？当任务序列可以预测,被试的准备与任务呈现方式之间的关系如何影响双任务协调中目标反应的策略执行效能？如何优化双任务加工？本研究将设计两种任务呈现方式(随机或固定),探讨任务呈现方式在双任务协调对策略执行影响中的作用。

1.4 问题提出

估算是重要的数学认知活动,日益受到研究者的重视。估算指个体一般未经过精确计算而只借助原有知识对问题提出粗略答案的一种估计形式,是心算、数概念和算术计算技巧之间相互作用的过程(司继伟,2002)。估算表现依赖于策略运用(司继伟等,2012)。因此,对估算策略心理机制的考察,可深化对人类一般数学能力的认识,甚至为数学概念、一般问题解决能力及策略的一般性理解的认识提供重要途径,有助于提高个体的数学估计甚至一般问题解决能力。与精算相比,估算这一算术形式的策略加工过程较简单(Kalaman&LeFevre,2007;Lemaire et al.,2000;LeFevre,Greenham,&Waheed,1993),且在不同数学任务形式中,已有大量研究使用估算这种算术计算形式来研究策略运用(加法：Lemaire&Lecacheur,2010;Uittenhove&Lemaire,2012;司继伟等,2014;乘法：Hinault et al.,2014;Taillan,Ardiale,&Lemaire,2015)。在加法估算中常采用有选/无选法范式开展策略研究(LeFevre et al.,1993;Siegler&Lemaire,1997;Lemaire et al.,2004;Lemaire&Lecacheur,2010;Uittenhove&Lemaire,2012,2013)。有选/无选法范式包含两个实验条件：有选条件和无选条件。Siegler和Lemaire(1997)认为该范式中的无选法提供了一种获得无偏估计策略表现特征的方法,即是考察策略执行的行为效能的良好方法。因此,本研究将选择/无选法范式中的无选条件和估算策略结合起来,在无选上调和无选下调两种条件下,要求被试执行相应的策略,通过考察策略执行的行为效能,进而探讨策略本身特征(正确性和反应时)对策略执行的影响。

基于已有研究,本研究拟探究双任务协调、任务呈现方式(随机或固定)对算术策略执行的影响。结合选择/无选法中的无选择条件和改进的PRP范式,通过控制任务呈现方式和反应数量,将任务呈现方式划分为随机与固定两种方式,来考察双任务协调对第一估算反应的策略执行效能的影响。实验1探讨随机呈现方式下,双任务协调对算术策略执行的影响;实验2则在固定呈现方式下,考察双任务协调对算术策略执行的影响,并比较随机和固定方式下的策略执行效能。Töllner等(2012)研究发现刺激序列的可预测性与否(固定呈现还是随机呈现)会影响到反应一,而Leonhard和Ulrich(2011)的研究发现中央加工序列是受准备与期待影响,刺激序列的可知与否对反应一的影响差异不大。根据认知龛理论,本研究假设,较随机呈现方式,在固定呈现方式中,由于各刺激的认知龛重合,被试有一定的准备和期望,使得估算的策略执行效能更好。

2 实验1随机呈现方式下,双任务协调对算术策略执行的影响

2.1 方法

2.1.1 被试

从山东省济南市高校随机选取大学生被试28人(年龄20～25岁之间,平均年龄24.2岁),其中两名被试未按要求作答,最后有效被试26人,视力正常或矫正视力正常,之前未接触类似实验,实验时间约45 min,实验结束后均赠送小礼物一份。

2.1.2 研究设计

采用2(单双反应：单反应,双反应)×2(任务呈现序列：数字先呈现,图形先呈现)×2(策略无选条件：无选/下调,无选/上调)三因素被试内实验设计。本研究分析的因变量有：估算反应时(估算任务正确时所花费的时间)、估算正确率(①双任务双反应条件下正确率的界定是：双反应中,被试正确采用提示策略得到并输入答案,记为正确的次数占总试次的百分比;②双任务单反应条件下正确率的界定是：单反应中,被试正确采用策略得到,输入答案记为正确的次数占总试次的百分比)和双任务协调代价(运用双反应的估算策略执行效能(RT,ACC)减去对应的单反应的策略执行效能(RT,ACC))(Lussier et al.,2012)(双任务−单反应和双任务−双反应的比较提供了双任务加工耗损的测量方式)。

2.1.3 实验任务

(1)估算任务。采用自编的两位数产生式加法任务(production tasks)。前人研究已证实,中央执行参与计算过程的进位操作,所占用工作记忆资源较多,会影响策略的执行(Caviola et al.,2012;Imbo et al.,2007;Imbo,Vandierendonck,&Vergauwe,2007)。为控制有无进位的差异,加数、被加数均为两位数,和均进位为三位数。自编两位数加法估算题目共144道,划分为4个Block,每一Block包含36道题(得分在117～162之间,平均值：134.69,标准差：13.05)。两位数加数图片像素为120×102,每次水平呈现于显示器屏幕中央。借鉴前人研究(Lemaire&Lecacheur,2010;Imbo,Duverne,&Lemaire,2007),要求被试采用上调策略和下调策略,依据指导语又快又准地输入估算答案。

(2)算术图形任务。采用修订心算测验(The Modified Mental Counters,MMC)(Ketelsen&Welsh,2010)中非言语干扰情景的3水平图片算术任务。MC最初由Larson和Sacuzzo(1989)发明,并分别由Seibert(2002)和Davis(2004)最早在研究中使用。刺激为灰底白色图片,像素为400×100,其中每条水平线代表5,初始状态三条水平线表示为555的数字串,当水平线上面出现白色方框时,代表对应水平线的数字5加上1,结果为6,当水平线下方出现白色方框时,代表对应水平线的数字5减去1,结果为4,则相应的输出结果也会出现变化。要求被试对3条水平线进行心算,然后输出变化后的数字串。以上两个任务中图形均为灰底白字,字体：Times New Roman,字号：48号,图形任务水平居中呈现于电脑屏幕中央。

(3)改进的PRP范式。一般的PRP范式采用刺激1(S1)−刺激2(S2)−反应1(R1)−反应2(R2)的呈现方式。本研究将其中的估算任务分开呈现,这就涉及到这两个加数是连续的呈现,还是中间存在刺激干扰的间隔情景下呈现。为更好地反应序列的影响,本研究首先规定无论序列顺序如何,需要先进行估算反应,再进行图形反应,因此本研究双任务范式采用的是图形算术任务(S1)−估算第一个操作数(S2a)−估算任务的第二个操作数(S2b)−估算反应(R2)−图形反应(R1)和估算第一个操作数(S2a)−图形算术任务(S1)−估算任务的第二个操作数(S2b)−估算反应(R2)−图形反应(R1)两种刺激呈现顺序与反应。

2.1.4 实验程序

采用E-Prime软件编写本实验程序、控制刺激呈现以及收集反应数据。范式为改进的PRP范式。正式实验前,被试先进行8个试次的练习,练习过程中提供反馈,以便让被试能够清楚了解实验流程。练习阶段的试次不参与分析。实验由加法估算任务与算术图形任务两个任务构成。采用改进的PRP范式与选择无选法中的无选条件研究范式,共包括4个Block,每一Block中任务呈现序列随机(数字先或图形先随机呈现),其中2个Block为双任务双反应测验,2个Block为双任务单反应测验。一半被试先进行双任务双反应,再进行双任务单反应;另一半被试的顺序相反。所有条件均在被试间进行平衡。

在安静实验室里,采用个别施测。正式实验时,首先,在电脑屏幕上呈现指导语,要求被试理解之后,按ENTER键后进入实验。每个trial过程如下：出现注视点“＋”500 ms提醒被试集中注意;待注视点消失后,呈现刺激1(图形任务/估算任务第一个运算数)500 ms,空屏300 ms;呈现刺激2(估算任务第一个运算数/图形任务)500 ms,空屏300～350 ms;呈现刺激3(估算任务第二个运算数),被试输入估算答案按ENTER键后消失,单反应任务进入空屏1000 ms,之后进入下一试次;双反应呈现空屏,要求在右下角白色方框内对图形任务反应按ENTER后消失,进入空屏1000 ms,进入下一试次(图1为数字先呈现单反应）。每一Block后,被试休息2～5 min,以缓解实验中的疲劳。

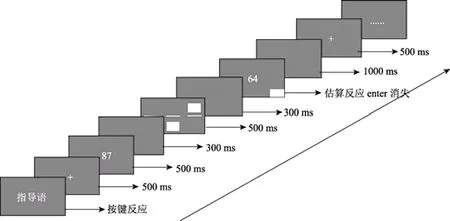
图1 数字先呈现单反应条件

2.1.5 数据处理

采用Excel 2007和SPSS 16.0对所获得的实验数据进行统计分析。数据指标有：各条件下估算反应时、正确率和双任务协调代价。

2.2 实验结果

2.2.1 不同实验条件下估算策略的策略执行效能

对估算任务的反应时和估算正确率分别进行2(单双反应：单反应,双反应)×2(任务呈现序列：数字先,图形先)×2(策略类型：无选/下调,无选/上调)重复测量方差分析(见表1)。结果显示：

a)正确率上,单双反应主效应显著(

(1,25)=83.00,

0.01,η=0.77),单反应显著高于双反应。策略类型主效应显著(

(1,25)=28.51,

0.01,η=0.53),估算下调策略显著高于上调策略。任务呈现序列主效应、任务呈现序列与单双反应交互作用、单双反应与策略类型交互作用、单双无选条件与任务呈现序列交互作用及其三者交互作用均不显著。b)反应时上,单双反应主效应显著(

(1,25)=48.73,

0.01,η=0.66),单反应估算显著快于双反应估算。任务呈现序列主效应显著(

(1,25)=41.33,

<0.01,η=0.62),数字先呈现显著长于图形先呈现。策略类型主效应显著(

(1,25)=48.05,

0.01,η=0.66),估算下调策略显著快于上调策略。单双反应与任务呈现序列交互效应显著(

(1,25)=14.87,

<0.01,η=0.37);进一步简单效应检验发现：数字先和图形先中,单反应均快于双反应(

(1,25)=65.08,

<0.01,η=0.72;

(1,25)=26.65,

<0.01,η=0.52);单反应中,数字先呈现和图形先呈现差异不显著,双反应中,数字先呈现显著长于图形先呈现(

(1,25)=42.87,

<0.01,η=0.63),而且双反应中,任务呈现序列的差异更大。单双反应与策略类型交互作用显著(

(1,25)=12.02,

<0.01,η=0.33)。进一步简单效应检验发现：不论单反应还是双反应中,下调策略显著短于上调策略(

(1,25)=18.09,

<0.01,η=0.43;

(1,25)=35.317,

<0.01,η=0.59); 不论无选下调条件还是无选上调,单反应估算显著短于双反应(

(1,25)=45.40,

<0.01,η=0.65;

(1,25)=32.86,

<0.01,η=0.59)。任务呈现序列与策略类型交互作用显著,

(1,25)=11.38,

<0.01,η=0.31;进一步简单效应检验发现,无选上调策略中,数字先呈现显著长于图形先出现,

(1,25)=56.38,

<0.01,η=0.69;无选下调策略中两者无显著差异;数字先出现和图形先出现中,上调策略显著均长于下调策略(

(1,25)=54.92,

<0.01,η=0.60;

(1,25)=18.15,

<0.01,η=0.42)。三者交互作用不显著。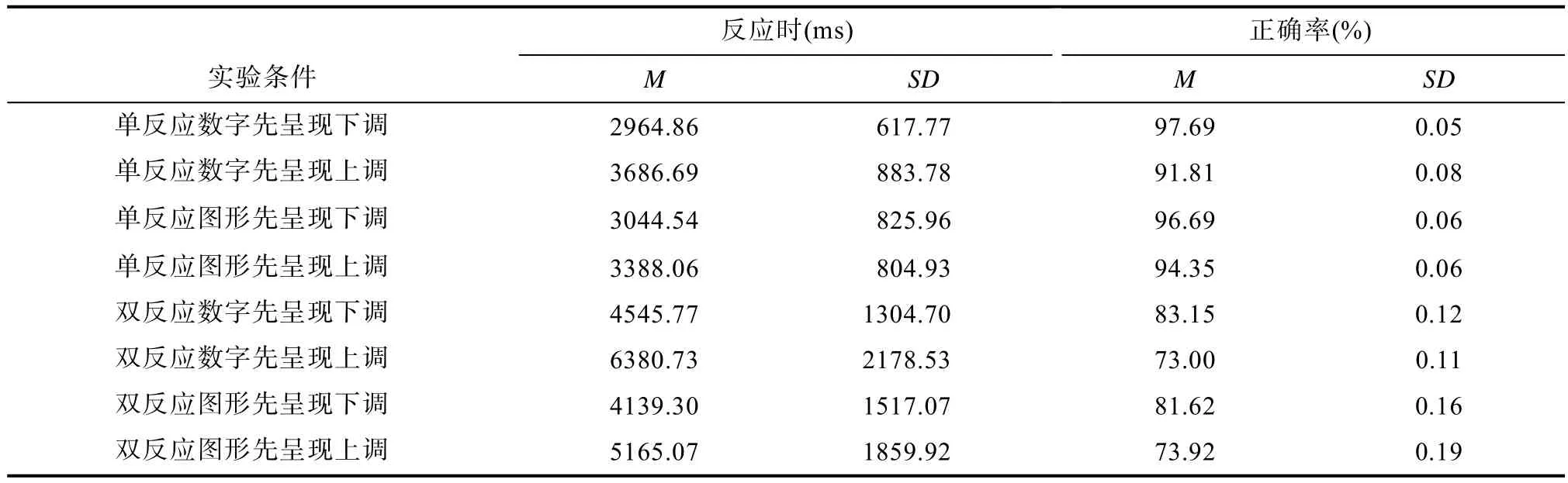

表1 各实验条件下被试估算策略的平均反应时及正确率

2.2.2 双任务协调代价中策略执行效能差异

对双任务协调代价的反应时和正确率采用(任务呈现序列：数字先,图形先)×2(策略类型：无选/下调,无选/上调)重复测量方差分析(见表2)。结果显示：a)正确率上,任务呈现序列主效应显著(

(1,25)=137.51,

<0.01,η=0.85),数字先呈现显著高于图形先呈现。策略类型主效应显著(

(1,25)=58.57,

0.01,η=0.70),下调策略显著低于上调策略。二者交互作用显著(

(1,25)=47.07,

<0.01,η=0.65),数字先呈现,下调策略显著高于上调策略(

(1,25)=125.05,

<0.01,η=0.83);而图形先呈现,上下调的差异不显著。下调中,数字先呈现显著高于图形先(

(1,25)=110.51,

<0.01,η=0.82),而在上调中两者差异不显著。b)反应时上,任务呈现序列主效应显著(

(1,25)=14.87,

0.01,η=0.37),数字先呈现的反应时差异显著长于图形先呈现。策略类型主效应显著(

(1,25)=12.02,

<0.01,η=0.33),下调策略显著低于上调策略。二者交互作用不显著。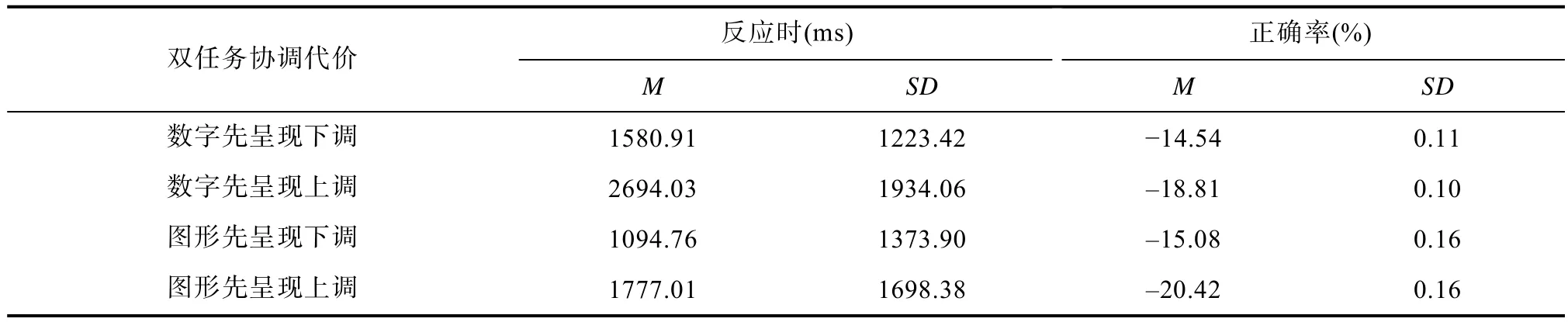

表2 双任务协调代价中被试估算策略的平均反应时及正确率

2.3 分析与讨论

随机呈现方式的行为结果表明,双任务协调情景对估算策略运用产生影响。策略本身的特性影响策略执行。本研究发现相较于下调策略,上调策略的反应时更长、错误率更高。Imbo,Vandierendonck,和De Rammelaere(2007)认为上调策略需要同时将两加数的十位数向上加一取整,相对于直接相加的下调策略,是较为复杂的策略,需要更多的认知资源。Lemaire等认为下调策略不需要增加操作数并在工作记忆中维持相应结果的额外步骤,所以简单;相反,上调策略则较复杂(Uittenhove&Lemaire,2012;Lemaire,Arnaud,&Lecacheur,2004;Lemaire&Lecacheur,2010)。因此,本研究与以往研究结果一致,均表明策略本身特征会影响策略的执行效能。

双任务协调影响估算策略执行效能(反应时与正确率),且对复杂策略影响更大。无论是无选上调策略,还是无选下调策略条件中,双反应的估算反应时显著长于单反应,双反应中上下调的差异比单反应更大,且双反应对上调策略的影响最大;正确率上,双反应也显著差于单反应。相对复杂的上调策略受到双反应的影响更大,这符合以往研究中的发现,需要更多加工步骤的策略较简单策略,在双任务中受到中央执行的影响更大(Imbo,Duverne,&Lemaire,2007;Imbo&Vandierendonck,2007;司继伟等,2012)。这说明中央执行的双任务协调在更复杂策略中需要更多地认知资源协调两个任务,对复杂程度不同的策略产生不同的影响。

虽然双任务协调对估算策略执行有影响,但任务呈现序列主效应显著,影响双任务的估算策略执行效能。数字先呈现的策略执行效能差于图形先呈现。本研究中,数字先呈现序列的两个操作数被图形任务隔开,个体需先将第一个操作数存储在记忆中,当第二个操作数呈现时,再将其提取出来后估算,存在估算任务的中断。图形先呈现序列中的两个操作数相继呈现,个体进行估算后,直接反应即可,估算任务所占用的认知资源较少。且本研究中要求先对数字估算反应,仅记录估算数字任务的反应时与正确率,因此,不论单双反应,数字先呈现占用的认知资源较多,其估算反应时长于图形先呈现。从双任务协调代价中可发现任务呈现序列、策略无选条件对估算策略执行效能产生影响,上调策略的双任务协调代价在反应时与正确率上都高于简单下调策略,数字先的双任务协调代价在反应时与正确率上都高于图形先。Töllner等(2012)研究发现刺激序列的可预测性与否会影响到反应一,而Leonhard和Ulrich(2011)的研究发现中央加工序列是由准备与期待影响,刺激序列的可知与否(固定序列还是随机序列)对反应一的影响差异不大。研究发现,序列随机呈现增加不可预测性,从而导致刺激序列对中央执行出现作用,不同呈现序列可能会存在序列难度效应,形成资源的相互占用与相互干扰。但是本研究中,作为反应一的估算任务双任务协调代价存在差异,该差异是由于随意性还是任务呈现序列的影响？这可能不是任务呈现序列差异,而是随机比固定所需要的双任务协调资源更大,因此随机方式所显示的任务呈现序列的影响,可能是由于随机导致的,而不是任务呈现序列本身。因此,为进一步明确策略执行过程中影响究竟是来自任务呈现序列还是任务呈现方式,我们在实验2中采用固定序列呈现方式进一步考察双任务协调对算术策略执行的影响。

3 实验2固定呈现方式下,双任务协调对算术策略执行的影响

3.1 方法

3.1.1 被试

在山东省济南市高校随机选取大学生被试30人(年龄19～23岁,平均年龄23.2岁),其中两名被试未按要求作答,最后有效被试28人,有效率93.3%,视力正常或矫正视力正常,之前未接触类似实验,实验时间约45 min,实验结束后均都赠送小礼物。

3.1.2 研究设计

采用2(单双反应：单反应,双反应)×2(任务呈现序列：数字先呈现,图形先呈现)×2(策略：下调,上调)三因素被试内实验设计,因变量为估算反应时、正确率和双任务协调代价。

3.1.3 测验材料和工具

实验任务和材料同实验1。

3.1.4 实验程序

实验程序与流程图都同实验1。不同在于实验2中任务呈现序列固定,每一Block中,其中一半被试先做数字先呈现序列任务,另一半先做图形先呈现序列任务;采用所有的条件均在被试间进行平衡。

3.1.5 数据处理

实验数据采用Excel 2007与SPSS 16.0分析。

3.2 实验结果

3.2.1 估算策略在不同实验条件下的策略执行效能差异

对估算任务的反应时和正确率分别进行2(单双反应：单反应,双反应)×2(任务呈现序列：数字先,图形先)×2(策略类型：无选/下调,无选/上调)的重复测量方差分析(见表3)。结果显示：

a)正确率上,单双反应主效应显著(

(1,27)=48.74,

0.01,η=0.64),单反应正确率显著高于双反应;任务呈现序列主效应、策略类型主效应及其二者、三者交互作用均不显著。b)反应时上,单双反应主效应显著(

(1,27)=26.67,

<0.01,η=0.50),单反应显著快于双反应。任务呈现序列主效应显著(

(1,27)=6.35,

<0.01,η=0.19),数字先出现显著长于图形先出现。策略类型主效应显著(

(1,27)=28.48,

0.01,η=0.51),下调策略显著快于上调策略。单双反应与策略类型交互作用显著(

(1,27)=5.66,

<0.05,η=0.17),进一步简单效应检验发现：下调策略和上调策略中,单反应估算显著短于双反应(

(1,27)=20.55,

0.01,η=0.43;

(1,27)=26.52,

0.01,η=0.50);单反应和双反应中,上调策略显著长于下调策略(

(1,27)=10.68,

0.01,η=0.28;

(1,27)=17.55,

0.01,η=0.39)。任务呈现序列和策略类型交互作用显著(

(1,27)=8.95,

<0.01,η=0.25),进一步简单效应检验发现,上调策略条件下,数字先出现显著长于图形先呈现(

(1,27)=13.27,

0.01,η=0.33),下调条件下数字先出现与图形先呈现差异不显著;数字先呈现和图形先呈现中,上调策略显著均长于下调策略(

(1,27)=31.17,

0.01,η=0.54;

(1,27)=13.12,

0.01,η=0.33)。三者交互作用不显著。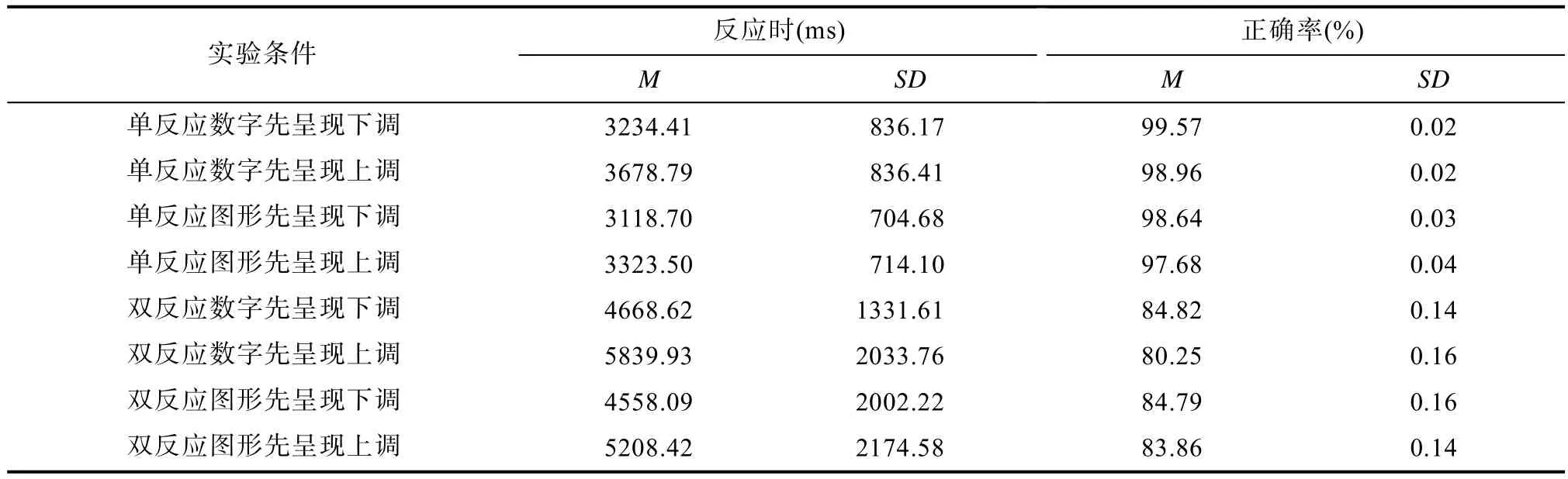

表3 各实验条件下被试估算策略的平均反应时与正确率

3.2.2 估算策略双任务协调代价的策略执行效能差异

对双任务协调代价的反应时和正确率进行2(任务呈现序列：数字先,图形先)×2(策略类型：无选/下调,无选/上调)的重复测量方差分析(见表4)。结果显示：

a)正确率上,任务呈现序列、策略类型主效应、二者交互作用均不显著。

b)反应时上,策略类型主效应显著(

(1,25)=5.66,

<0.05,η=0.17),下调策略显著低于上调策略。其余效应均不显著。

3.2.3 不同呈现方式下,被试估算策略的反应时和正确率

以实验1和实验2中的被试策略执行的执行效能(RT、ACC、双任务协调代价)为因变量,以任务呈现方式(随机/固定)为被试间变量,任务呈现序列(数字先/图形先)、反应类型(单/双反应)和策略类型(上/下调)为被试内变量,进行重复测量方差分析(见表5),结果显示：策略执行效能中正确率上,任务呈现方式主效应显著(

(1,52)=6.17,

=0.02,η=0.11);反应时上,任务呈现方式主效应不显著(

(1,52)=0.02,

=0.88)。以上结果表明,任务呈现方式影响策略执行。双任务协调代价中正确率上,任务呈现方式的主效应显著(

(1,52)=6.03,

=0.02,η=0.10);反应时上,任务呈现方式主效应不显著(

(1,52)=0.02,

=0.90)。该结果表明,任务呈现方式不仅影响策略执行,而且也影响双任务协调。

3.3 分析与讨论

固定呈现方式的行为结果表明,双任务协调情景对估算策略执行产生影响。策略类型、单双反应、任务呈现序列影响估算策略执行反应时与正确率,这都与实验1随机呈现方式的结果相同。无论单双反应,数字先呈现的估算反应时长于图形先呈现估算,上调策略的反应时长于下调策略,说明上调策略的复杂性高于下调策略,数字先的任务难度高于图形先。难度较大,需要更多的认知资源。但与实验1不同的是,固定呈现方式下,单双反应与任务呈现序列间交互作用消失。当任务呈现序列固定或可预测时,对单双反应有影响,但未对策略类型产生实质影响。说明准备与先进入先加工可能单独影响策略中央执行序列,而在随机呈现方式中则可能同时存在,即任务呈现方式对双任务协调代价有影响,且不受策略类型的影响。值得注意的是,实验2中双任务协调代价在策略无选条件效应显著,其余效应均消失,这与随机呈现方式下的结果差异较大,序列间不一致较一致需要更多注意控制与双任务协调,随机呈现方式对估算策略执行的影响相比固定方式的影响更大。固定呈现方式中被试是依据准备与期待进行的双任务加工,受任务呈现方式的外在刺激序列的影响相对较少。该结果进一步表明,相较于先进入先加工,准备与期待对中央执行序列影响会更大(Leonhard&Ulrich,2011;Szameitat,Lepsien,von Cramon,Sterr,&Schubert,2006;Töllner et al.,2012)。

表4 双任务协调代价中被试估算策略的平均反应时及正确率

表5 不同序列呈现方式下,被试估算策略的反应时和正确率

4 总讨论

本研究在随机和固定两种不同呈现方式下,探讨了双任务协调对算术策略执行的影响。两项实验均表明策略无选条件、单双反应、任务呈现序列、双任务协调影响估算策略执行的行为效能。这符合前人有关发现,即双任务协调与策略类型的交互作用、与反应类型的交互作用都对策略执行有影响,工作记忆资源对策略执行的影响在执行复杂策略时更为明显(Imbo,Duverne,&Lemaire,2007;蒋姝,李娜,2011)。与实验1所不同的是,实验2在双任务协调代价这一变量上,除策略无选条件效应的显著性仍保持,其余效应均消失。随着任务呈现序列的固定,任务呈现方式对双任务协调具有一定的作用。固定方式下,相同的环境,可促使个体提前准备和具有一定的期望(Leonhard&Ulrich,2011),这有助于在双任务中进行协调,进而提高策略的执行效能。

双任务协调影响策略执行的执行效能。不论任务呈现方式如何,实验1和实验2结果均表明策略执行中单双反应(RT、ACC)的主效应显著,双反应的策略执行效能均差于单反应的策略执行效能。Lussier等(2012)的研究设计中,单双任务是根据反应类型区分的,分为双任务单反应和双任务双反应两种反应类型。由于单双反应均涉及中央执行的转化、抑制和刷新功能,那么两者的差异则归因于双任务协调的影响。本研究中,反应类型的差异表明了双任务协调的影响。即本研究中,反应类型的显著性差异表明了双任务协调对策略执行的影响。而双任务协调过程会占用额外的认知资源,导致个体在双反应条件下的反应变慢、正确率降低。

任务呈现方式影响策略执行效能。本研究中任务呈现序列对策略执行的影响随着随机到固定的变化而消失,随机相对于固定需要启动与转换认知资源,出现认知资源额外占用情景(Leonhard&Ulrich,2011),支持在数字策略执行中可能存在认知资源的有限性。该额外占用的认知资源可能是由于伴随随机方式所出现的刺激的序列难度效应,而在固定重复方式中策略执行效能减少了这种序列难度。这符合Leonhard和Ulrich(2011)的观点,即刺激序列、准备都会影响中央加工序列。这种中央加工序列灵活决断会允许双任务协调情境中出现合适的甚至优化加工,出现优化中央加工序列。任务呈现方式的影响具有重要意义,在双任务协调中,刺激序列的变化会影响到策略的执行效能,而且在策略表现中需要考虑到任务呈现方式的影响。

本研究中随机呈现方式的策略执行正确率显著低于固定呈现方式,表明任务呈现方式影响策略执行,随机方式的策略执行效能较固定方式差。根据认知龛理论(Marewski&Schooler,2011)的观点,本研究中任务呈现方式为策略的执行提供两种情景：固定呈现方式和随机呈现方式。固定呈现方式下,当前情境与前一试次中的认知龛重合,本着先进入先加工的原则,个体根据先前试次序列,已做好反应准备,正确处理双任务间的反应顺序,进行双任务间的协调,无需进行重新的判断与决策,缩短了对两个任务间加工过程及策略执行过程的协调,占用的认知资源少,反应时快,正确率高(Leonhard&Ulrich,2011)。而在随机呈现方式下,与前一试次情景的认知龛不重合,个人任务加工的准备状态与当前情境冲突,个体需重新对双任务进行协调,做好先进入先加工的准备,并对加工的结果进行保存,此时的认知资源占用较多,个体的反应变慢,正确性低(张俊,刘儒德,2011)。该研究结果与Szameitat等(2002)的研究一致,即在随机方式下的激活更大,占用的认知资源较多(Szameitat et al.,2002,2006)。认知龛理论认为策略的可用性应是认知系统与环境之间相互作用的函数,策略选择是基于个人的认知系统(主要是努力程度、时间和准确性)和环境的交互作用(Marewski&Schooler,2011;张俊,刘儒德,2011)。正如本研究中发现的任务呈现方式会影响个体的策略执行效能,即准备与期望在其中的作用。因此,本研究认为认知龛理论中的认知系统不仅仅是努力程度,还应包含个体的准备状态和期望。新近研究已显示,工作记忆会明显制约策略执行,如导致策略执行中的序列难度效应(Schneider&Anderson,2010;Uittenhove&Lemaire,2012,2013)。策略的选择和执行是相当复杂的认知加工过程,要从理论上阐释清楚其运作机制,不应只考虑环境和简单的认知系统(如努力程度、时间和准确性)的作用,也要考虑其他认知因素(如工作记忆、准备、期望等)的影响。

综合本研究结果可发现,双任务协调、任务呈现方式影响估算策略执行效能,策略类型、单双反应都会对估算策略执行产生影响,但随机方式需要的策略执行效能的双任务协调代价显著高于固定方式。固定方式很好地表明有效的准备与期待(单双反应与固定序列)使得双任务协调对策略执行效能产生影响,基于Leonhard和Ulrich(2011)的预测当刺激序列100%固定,被试准备足以成功处理双任务,则双任务协调代价减少甚至消失。为处理复杂双任务情景提供借鉴,良好的准备与期待会为复杂任务带来成功,而且不能忽视中断任务的重要影响,其会耗费更大的资源进行重新加工,需要我们注意任务的连贯性。而且双任务耗损显著高于单任务,需要我们合理分配精力,对于多任务处理中,最好分出重要与次要,以便优化加工序列,保证任务的更好完成。并且双任务协调中,固定方式的预测性和被试准备的增加,策略执行的行为效能提高,说明对中央执行认知资源的需求降低,使得个体具有更好协调双任务的能力。当同时运用中央执行其他功能时,也会分配更多资源进行处理,从而有助于其它执行功能的执行。有趣的是,在双任务协调代价这一变量上,随着任务呈现方式的固定,其策略执行效能存在差异。数字先呈现中,随机的双任务代价大于固定;图形先呈现中,固定的双任务代价大于随机(见表5)。说明任务呈现方式与双任务协调存在交互作用,且该交互作用不受策略本身特征的影响。那么,二者的交互作用是如何实现的？是呈现方式通过双任务协调间接作用于策略执行,还是两者共同对其产生影响？这都有待于进一步探讨。

本研究的不足与局限主要表现在：首先,本研究固定反应顺序且只记录了反应一的反应时,即估算,未记录图形任务的反应时,无法比较两种任务的行为效能、双任务协调对先呈现任务的影响及任务呈现序列对两种任务的影响。其次,本研究通过Block控制了反应类型,并未实现反应类型的随机化,可在设置一个实验将单双反应这一变量实现随机化,检验在双任务中是否有差异,以实现双任务协调的完全随机。最后,本研究未进一步探讨试次间策略执行的相互影响。已有研究发现在算术策略执行中,存在较差策略效应的序列调整,该序列效应会影响策略的执行(Hinault et al.,2014;Schneider&Anderson,2010;Uittenhove&Lemaire,2013)。不论是随机方式还是固定方式,本研究中前一试次的策略是否为最佳策略,是否对当前试次的策略执行有影响均未进行进一步的探讨,在以后的研究中应适当的控制该类策略序列效应。

Baddeley,A.D.(1996).Exploring the central executive.

The Quarterly Journal of Experimental Psychology A,49

(1),5–28.Baddeley,A.D.(2012).Working memory:Theories,models,and controversies.

Annual Review of Psychology,63

,1–29.Benjamin,A.S.&Bird,R.D.,(2006).Metacognitive control of the spacing of study repetition.

Journal of Memory and Language,55

(1),126–137.Bull R.,Johnston R.S.,&Roy J.A.(1999).Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills:Views from cognition and developmental neuropsychology.

Developmental Neuropsychology,15

(3),421–442.Caviola,S.,Mammarella,I.C.,Cornoldi,C.,&Lucangeli,D.(2012).The involvement of working memory in children’s exact and approximate mental addition.

Journal of Experimental Child Psychology,112

(2),141–160.Cepeda,N.J.,Pashler,H.,Vul,E.,Wixted,J.,&Rohrer,D.(2006).Distributed practice in verbal recall tasks:A review and quantitative synthesis.

Psychological Bulletin,132

(3),354–380.Chen,T.Y.,&Li,D.M.(2005).The diversity of executive functions in normal adults:A latent variable analysis.

Acta Psychologica Sinica,37

(2):210–217.[陈天勇,李德明.(2005).执行功能可分离性及与年龄关系的潜变量分析.

心理学报,37

(2),210–217.]Chen,Y.H.,&Wang,M.Y.(2009).The relationship between executive functions and arithmetical cognitive strategies of children.

Psychological Science,32

(1),34–37.[陈英和,王明怡.(2009).儿童执行功能与算术认知策略的关系.

心理科学,32

(1),34–37]Collette,F.,&van der Linden M.(2002).Brain imaging of the central executive component of working memory.

Neuroscience and Biobehavioral Reviews,26

(2),105–125.Davis,D.(2004).

Working memory and inhibition:A test of the duality of the central executive

(Unpublished master’s thesis).University of Northern Colorado.Hinault,T,Dufau,S,& Lemaire,P,(2014).Sequential modulations of poorer-strategy effects during strategy execution:An event–related potential study in arithmetic.

Brain and Cognition,91

,123–130.Imbo,I.,Duverne,S.,&Lemaire,P.(2007).Working memory,strategy execution,and strategy selection in mental arithmetic.

The Quarterly Journal of Experimental Psychology,60

(9),1246–1264.Imbo,I.,& LeFevre,J.A.(2009).Cultural differences in complex addition:Efficient Chinese versus adaptive Belgians and Canadians.

Journal of Experimental Psychology:Learning,Memory,and Cognition,35

(6),1465–1476.Imbo,I.,& Vandierendonck,A.(2007).The role of phonological and executive working memory resources in simple arithmetic strategies.

European Journal of Cognitive Psychology,19

(6),910–933.Imbo,I.,Vandierendonck,A.,&De Rammelaere,S.(2007).The role of working memory in the carry operation of mental arithmetic:Number and value of the carry.

The Quarterly Journal of Experimental Psychology,60

(5),708–731.Imbo,I.,Vandierendonck,A.,&Vergauwe,E.(2007).The role of working memory in carrying and borrowing.

Psychological Research,71

(4),467–483.Iuculano,T.,Moro,R.,&Butterworth,B.(2011).Updating working memory and arithmetical attainmentin school.

Learning and Individual Differences,21

(6),655–661.Jiang,S.,&Li,N.(2011).Strategy in mental arithmetic:Studiesfrom cognition.

JournalofJiangsu Teachers University of Technology,17

(2),12–17.[蒋姝,李娜.(2011).心算加工策略的认知科学研究综述.

江苏技术师范学院学报,17

(2),12–17.]Kalaman,D.A.,&LeFevre,J.A.(2007).Working memory demands of exact and approximate addition.

European Journal of Cognitive Psychology,19

(2),187–212.Ketelsen,K.,&Welsh,M.(2010).Working memory and mental arithmetic:A case for dual central executive resources.

Brain and Cognition,74

(3),203–209.Larson,G.E.,&Sacuzzo,D.P.(1989).Cognitive correlates of general intelligence:Toward a process theory of

Intelligence,13

(1),5–31.LeFevre,J.A.,Greenham,S.L.,&Waheed,N.(1993).The development of procedural and conceptual knowledge in computational estimation.

Cognition and Instruction,11

(2),95–132.Lemaire,P.,Arnaud,L.,& Lecacheur,M.(2004).Adults'age-related differences in adaptivity ofstrategy choices:Evidence from computational estimation.

Psychology and Aging,19

(3),467–481.Lemaire,P.,&Callies,S.(2009).Children’s strategies in complex arithmetic.

Journal of Experimental Child Psychology,103

(1),49–65.Lemaire,P.,&Lecacheur,M.(2010).Strategy switch costs in arithmetic problem solving.

Memory and Cognition,38

(3),322–332.Lemaire,P.,Lecacheur,M.,&Farioli,F.(2000).Children’s strategy use in computational estimation.

Canadian Journal of Experimental Psychology,54

(2),141–148.Lemaire,P.,&Reder,L.(1999).What affects strategy selection in arithmetic?The example of parity and five effects on product verification

.Memory and Cognition,27

(2),364–382.Leonhard,T.,&Ulrich R.(2011).Determinants of central processing order in psychological refractory period paradigms:Central arrival times,detection times,or preparation?.

The Quarterly JournalofExperimentalPsychology,64

(10),2012–2043.Liepelt,R.,Strobach,T.,Frensch,P.,&Schubert,T.(2011).Improved intertask coordination after extensive dual-task practice.

The Quarterly Journal of Experimental Psychology,64

(7),1251–1272.Liu,P.D.,Yang,W.J.,Tian,X.,&Chen,A.T.(2011).An overview of current studies about the conflict adaptation effect.

Advances in Psychological Science,20

(4),532–541.[刘培朵,杨文静,田夏,陈安涛.(2011).冲突适应效应研究述评.

心理科学进展,20

(4),532–541.]Logie,R.H.,Cocchini,G.,Della Sala,S.,&Baddeley,A.D.(2004).Is there a specific executive capacity for dual task coordination? Evidence from Alzheimer’s disease.

Neuropsychology,18

(3),504–513.Luo,L.L.,&Zhou,X.L.(2004).Executive function and number processing:A review.

Advances in Psychological Science,12

(5),714–722.[罗琳琳,周晓林.(2004).执行功能与数量加工:回顾与展望.

心理科学进展,12

(5),714–722.]Lussier,M.,Gagnon,C.,&Bherer,L.(2012).An investigation of response and stimulus modality transfer effects after dual-task training in younger and older.

Frontiers in Human Neuroscience,6

,129,doi:10.3389/fnhum.2012.00129.Marewski,J.N.,&Schooler,L.J.(2011).Cognitive niches:An ecological model of strategy selection.

Psychological Review,118

(3),393–437.Mata,R.,Josef,A.K.,&Lemaire,P.(2015).Chapter 6-Adaptive decision making and aging.In T.M.Hess,J.Strough,&C.Lckenhoff(Eds.),

Aging and decision making:Empirical and applied perspectives

(pp.105–122).New York:Academic Press.Mata,R.,Schooler,L.J.,&Rieskamp,J.(2007).The aging decision maker:Cognitive aging and the adaptive selection of decision strategies.

Psychology and Aging,22

(4),796–810.Miller,J.,Ulrich,R.,&Rolke,B.(2009).On the optimality of serial and parallel processing in the psychological refractory period paradigm:Effects of the distribution of stimulus onset asynchronies.

Cognitive Psychology,58

(3),273–310.Miyake,A.,Friedman,N.P.,Emerson,M.J.,Witzki,A.H.,Howerter,A.,&Wager,T.D.(2000).The unity and diversity of executive functions and their contributions to complex frontal lobe tasks:A latent variable analysis.

Cognitive Psychology,41

(1),49–100.Navon,D.,&Miller,J.(1987).Role of outcome conflict in dual-task interference.

Journal of Experimental Psychology:Human Perception and Performance,13

(3),435–448.Noel,M.P.(2009).Counting on working memory when learning to count and to add:A preschool study.

Developmental Psychology,45

(6),1630–1643.Olszanowski,M.,Bajo,M.T.,&Szmalec,A.(2015).A conflict monitoring account of the control mechanisms involved in dual-tasking.

Journal of Cognitive Psychology,27

(6),704–714.Pashler,H.(1994).Dual-task interference in simple tasks:Data and theory.

Psychological Bulletin,116

(2),220–244.Pashler,H.,&Johnston,J.C.(1998).Attentional limitations in dual-task performance.In:H.Pashler(Ed.),

Attention

(pp.155–189).Hove:Psychology Press.Raghubar,K.P.,Barnes,M.A.,&Hecht,S.A.(2010).Working memoryand mathematics:A review ofdevelopmental,individual difference,and cognitive approaches.

Learning and Individual Differences,20

(2),110–122.Rieskamp,J.,&Otto,P.E.(2006).SSL:A theory of how people learn to select strategies.

Journal of Experimental Psychology:General,13

5(2),207–236.Roediger,H.L.,&Karpicke,J.D.(2006).The power of testing memory:Basic research and implications for educational practice.

Perspectives on Psychological Science,1

(3),181–210.Schneider,D.W.,&Anderson,J.R.(2010).Asymmetric switch costs as sequential difficulty effects.

The Quarterly Journal of Experimental Psychology,63

(10),1873–1894.Seibert,T.M.(2002).

Working memory and inhibition a limited capacity system:A test of the separability of verbal and nonverbal resources

(Unpublished master’s thesis)

University of Northern Colorado.Shrager,J.,&Siegler,R.S.(1998).SCADS:A model of children's strategy choices and strategy discoveries.

Psychological Science,9

(5),405–410.Si,J.W.(2002)

.Computational estimation competence of primary school children

(Unpublished doctoral dissertation)

Southwest China Normal University,Chongqing.[司继伟.(2002).

小学儿童估算能力研究

(博士学位论文).西南师范大学,重庆.]Si,J.W.,Xu,Y.L.,Feng,H.M.,Xu,X.H.,&Zhou,C.(2014).Differences of arithmetic strategy use in adults with different math anxieties:An ERP study.

Acta Psychologica Sinica,46

(12),1835–1849.[司继伟,徐艳丽,封洪敏,许晓华,周超.(2014).不同数学焦虑成人的算术策略运用差异:ERP研究.

心理学报,46

(12),1835–1849.]Si,J.W.,Yang,J.,Jia,G.J.,&Zhou,C.(2012).The effect of central executive load on adult’s strategy using in computational estimation.

Acta Psychologica Sinica,44

(11),1490–1500.[司继伟,杨佳,贾国敬,周超.(2012).中央执行负荷对成人估算策略运用的影响.

心理学报,44

(11),1490–1500.]Siegler,R.S.(2007).Cognitive variability.

Developmental Science,10

(1),104–109.Siegler,R.S.,&Araya,R.(2005).A computational model of conscious and unconscious strategy discovery.In R.V.Kail(Ed.),

Advances in child development and behavior

(Vol.33,pp.1–42).San Diego,CA:Elsevier Inc.Siegler,R.S.,&Lemaire,P.(1997).Older and younger adults'strategy choices in multiplication:Testing predictions of ASCM using the choice/no-choice method.

Journalof Experimental Psychology:General,26

(1),71–92.Sigman,M.,&Dehaene,S.(2006).Dynamics of the central bottleneck:Dual-task and task uncertainty.

PLoS Biology,4

(7),e220.Son,L.K.(2010).Metacognitive control and the spacing effect.

Journal of Experimental Psychology:Learning,Memory,and Cognition,36

(1),255–262.Strobach,T.,Frensch,P.,Müller,H.,&Schubert,T.(2012).Age-and practice-related influences on dual-task costs and compensation mechanisms underoptimalconditions of dual-task performance.

Aging,Neuropsychology,and Cognition,19

(1–2),222–247.Swanson,H.L.,Jerman,O.,&Zheng,X.H.(2008).Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties.

Journal of Educational Psychology,100

(2),343–379.Szameitat,A.J.,Schubert,T.,Müller,K.,&von Cramon,D.Y.(2002).Localization of executive functions in dual-task performance with fMRI.

Journal of Cognitive Neuroscience,14

(8),1184–1199.Szameitat,A.J.,Lepsien,J.,von Cramon,D.Y.,Sterr,A.,&Schubert,T.(2006).Task-order coordination in dual-task performance and the lateral prefrontal cortex:An event-related fMRI study.

Psychological Research,70

(6),541–552.Taillan,J.,Ardiale,E.,&Lemaire,P.(2015).Relationships between strategy switching and strategy switch costs in young and older adults:A study in arithmetic problem solving.

Experimental Aging Research,41

:136–156.Töllner,T.,Strobach,T.,Schubert,T.,&Müller,H.J.(2012).The effect of task order predictability in audio-visual dual task performance:Just a central capacity limitation?.

Frontiers in Integrative Neuroscience,6

,75,doi:10.3389/fnint.2012.00075.Toppino,T.C.,Cohen,M.S.,Davis,M.L.,&Moors,A.C.(2009).Metacognitive control over the distribution of practice:When is spacing preferred?.

Journal of Experimental Psychology: Learning,Memory,and Cognition,35

(5),

1352

–1358Torbeyns,J.,Verschaffel,L.,&Ghesquière,P.(2005).Simple addition strategies in a first-grade class with multiple strategy instruction.

Cognition and Instruction,23

(1),1–21.Uittenhove,K.,&Lemaire,P.(2012).Sequential difficulty effects during strategy execution.

Experimental Psychology,59

(5),295–301.Uittenhove,K.,&Lemaire,P.(2013).Strategy sequential difficulty effects vary with working-memory and responsestimulus-intervals:A study in arithmetic.

Acta Psychologica,143

(1),113–118.Wang,M.Y.,&Chen,Y.H.(2006).The influence of central executive of working memory on children’s arithmetical cognitive strategies.

Psychological Development and Education,22

(4),24–28.[王明怡,陈英和.(2006).工作记忆中央执行对儿童算术认知策略的影响.

心理发展与教育,22

(4),24–28.]Yang,J.,Li,Y.H.,Si,J.W.,&Zhang,M.L.(2011).Central executive component affects adults'computational estimation performance.

Psychological Exploration,31

(4),314–317,325.[杨佳,李颖慧,司继伟,张明亮.(2011).工作记忆中央执行成分对估算表现的影响.

心理学探新,31

(4),314–317,325.]Zhang,J.,&Liu,R.D.(2011).Process and influence factors of learning strategy selection.

Journal of Beijing Normal University(Social Science),

(6),21–29.[张俊,刘儒德.(2011).学习策略选择的过程与影响因素.