四参数Logistic模型潜在特质参数的Warm加权极大似然估计*
2016-02-01孟祥斌陈莎莉
孟祥斌 陶 剑, 陈莎莉
(1东北师范大学教育学部; 2东北师范大学数学与统计学院, 应用统计教育部重点实验室;3中国基础教育质量监测协同创新中心东北师范大学分中心, 长春 130024)
1 引言
近30年来, 随着统计和计算机技术的飞速发展, 项目反应理论(Item Response Theory, IRT)的研究和应用取得了长足的进步。时至今日, 它已取代经典测量理论成为测量学研究的核心内容, 并在考试测评的诸多领域发挥着重要的作用。
在IRT中, 单维二值评分模型的理论和技术最为成熟, 应用也最为广泛。二值记分模型通常假设被试的潜在特质参数与反应的正确概率之间满足Logistic函数或者Probit函数关系。这两类模型在一定程度上是等价的, 但Logistic模型因其参数估计容易计算而广受青睐, 成为IRT领域最为重要的一族模型。根据项目参数个数的不同, 常用的Logistic模型分为单参数、两参数和三参数(1PL, 2PL和3PL)模型。模型包含的参数越多, 模型所描述的现象就越广泛, 但参数估计对算法的要求也会越高。近年来, 随着IRT理论体系的日趋完善, 测量学者们开始努力尝试四参数Logistic (4-Parameter Logistic, 4PL)模型的理论与应用研究。
四参数模型的构想最早是由Barton和Lord在1981年提出的, 目的是为了考虑高能力被试作答失误的可能, 他们建议在3PL模型的基础上加入一个小于1的项目特征曲线上渐近线参数。最初该参数被限定为公共参数, 与项目无关。随后一些研究发现(Linacre, 2004; Rupp, 2003; Tavares, de Andrade,& Pereira, 2004; Waller &Reise, 2009)不同项目特征曲线的上渐近线是存在差异的, 上渐近线参数被定义为项目参数更加科学。于是, 4PL模型的表达式为,
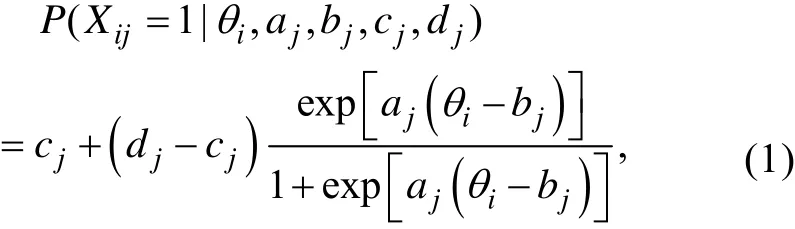

长期以来, 4PL模型的发展速度都非常缓慢,一直没有引起测量学界的广泛关注。主要原因是4PL模型的参数估计没有被很好解决, 难以满足测试的实际需要, 进而导致4PL模型的实际价值也没有得到充分验证。近些年, 关于4PL模型的理论与应用研究相继取得一些突破性的研究成果, 例如,Linacre (2004)和Rupp (2003)对上渐近线参数的价值进行了深入的讨论, 并给出了参数估计的计算方法。Loken和Rulison (2010)给出了4PL模型参数贝叶斯估计的Markov chain Monte Carlo (MCMC)算法, 有效解决了4PL模型项目参数的标定, 这对4PL模型的使用具有重要意义。Rulison和Loken (2009)验证了, 在计算机自适应测试(computerized adaptive testing, 简称CAT)中, 使用4PL模型能够提高被试潜在特质参数估计的精度。随后, Green(2011), Liao,Ho, Yen和Cheng (2012)、Yen, Ho, Liao, Chen和Kuo(2012)相继从多方面对4PL模型在CAT环境中的应用进行了更为深入的研究, 所得结果均表明4PL模型要优于传统的3PL模型。Magis(2013)对4PL模型信息函数的性质进行了系统研究, 并给出一种信息函数最大值点的求解方法。此外, 在其它领域,4PL模型也有诸多成功地实践, 如有兴趣可查看以下文献(Osgood, McMorris, &Potenza, 2002; Waller&Reise,2009; Tavares et al., 2004)。综上所述, 无论是从方法论的角度, 还是基于实用性的目的, 4PL模型均具有极大的潜力和较高的应用价值。可以预见, 随着4PL模型理论体系的日趋完善, 它必将成为未来主流的IRT模型之一, 在心理和教育测量的诸多领域发挥着不可替代的作用。
潜在特质参数的估计是IRT的主要内容之一,常用的方法有以下3种:(1)极大似然估计(maximum likelihoodestimate, MLE); (2)后验期望估计(expected a posteriori estimate, EAPE); (3)最大后验概率估计(maximum a posterioriestimate, MAPE)。在实际应用中, MLE和EAPE是最常用的两种估计方法, 它们具备优良的大样本性质。但是, 如果测试项目较少,将导致MLE和EAPE的效能降低, 难以保证估计的无偏性和准确性。潜在特质参数估计的无偏性对项目反应模型的应用非常重要, 如果参数估计的偏差较大, 将给进一步更为深入的测评带来严重误差(Warm, 1989;Penfield& Bergeron, 2005; Magis, 2014)。针对MLE和EAPE的这一不足, Warm在1989年提出一种3PL模型潜在特质参数的加权极大似然法,降低了估计的偏差。随后, Wang和Wang (2001)以及Penfield和Bergeron (2005)分别在CAT和线性测试环境下, 把Warm的加权极大似然估计(weighted maximum likelihoodestimator, WMLE)推广到广义局部评分模型(generalized partial credit model, GPCM),并验证了WMLE的优越性。
借鉴已有研究经验, 本文以4PL模型为研究对象, 对其潜在特质参数的WMLE进行研究。首先,根据4PL模型的结构特点, 给出加权函数的构造公式。然后, 对加权极大似然方程的求解过程进行推导。最后, 通过计算机模拟在不同测试条件下对4PL模型潜在参数的WMLE、MLE和EAPE的性质进行比较, 以验证WMLE的优越性。希望通过本文的研究, 能够为4PL模型的应用提供科学而有效的参数估计技术。
2 方法
这部分首先对4PL模型潜在特质参数的MLE进行简要介绍; 然后, 引出4PL模型潜在特质参数的WMLE并对相关计算过程进行详细推导; 最后, 简要给出4PL模型下潜在特质参数EAPE的计算公式。
2.1 极大似然估计(MLE)
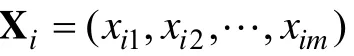
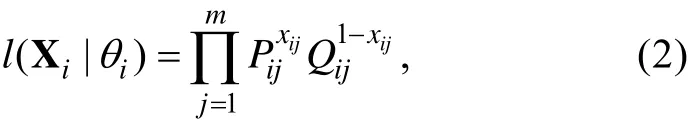
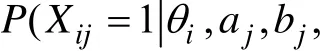
对方程(2)两端取自然对数得到对数似然函数,

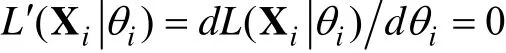
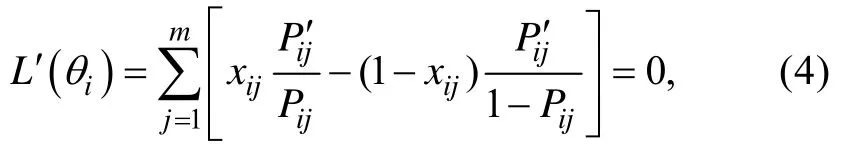
因为该方程为非线性方程, 通常使用Newton-Raphson(N-R)迭代算法对其进行求解。
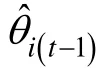

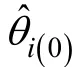
2.2 加权极大似然估计(WMLE)
令l
表示加权似然函数, 根据加权似然的定义有
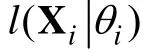
对方程(12)两端取自然对数得对数加权似然函数为,

f
(θ
)必须且只需满足以下等式条件,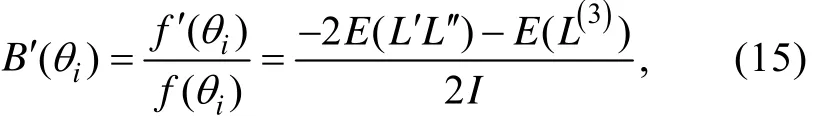

f
(θ
)是非常困难的, 而且满足条件的f
(θ
)也不唯一, 但这并不会阻碍WMLE的求解。由方程(14)可知, 只要能够推导出B
′(θ
),加权似然方程(14)随之确定, 整个过程f
(θ
)是不必知道的。因此, 本研究首先要解决的问题是对4PL模型下的B
′进行推导, 然后再给出求解加权似然方程的N-R迭代算法。可以证明, 对于4PL模型有以下等式成立,
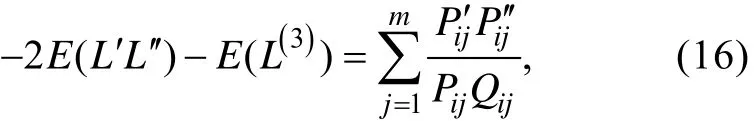
详细证明过程请参见附录。
根据方程(1)、(8)和(9)可得方程(16)的具体形式为,
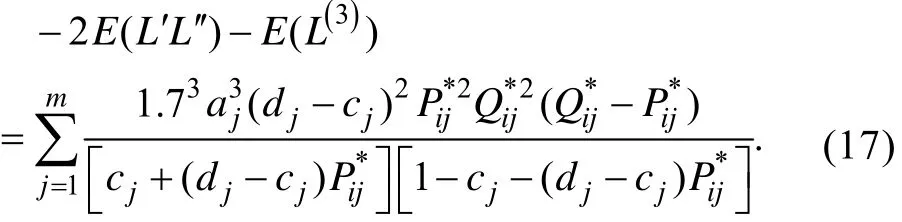
I
(θ
)的定义有,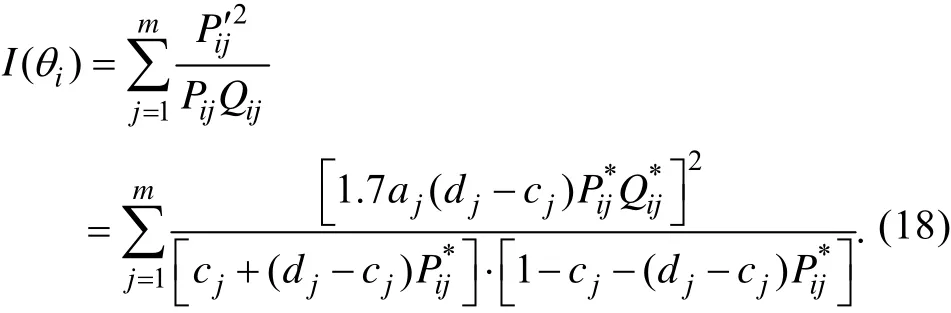
最后, 将方程(17)和(18)代入方程(15),
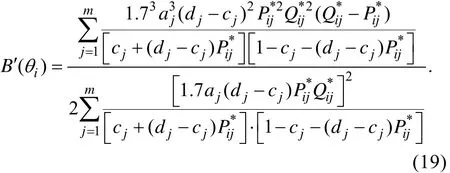
对方程(19)和方程(4)进行求和, 即可得到4PL模型的Warm加权似然方程(14),由于该方程过于繁琐, 这里就不给出它的具体形式了。
本研究采用N-R算法对4PL模型能力参数的Warm加权似然方程进行求解。根据定义, 4PL模型下方程(14)的N-R迭代公式如下,

其中,


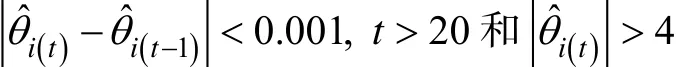
2.3 后验期望估计(EAPE)
EAPE与MLE相比, 优势是对于极端的反应数据表现比较稳定且容易计算, 不足是EAPE的偏差较大, 容易受到错误先验信息的影响。一般来说,当测试的项目数较少时, 建议使用EAPE, 在项目数较多时, MLE更受青睐。
在IRT中,θ
的先验分布通常选取为标准正态分布, 其密度函数记为φ
(θ
).根据定义, 标准正态先验下的EAPE的计算公式如下,
θ
的后验概率密度函数。将方程(27)代入方程(26), 整理得
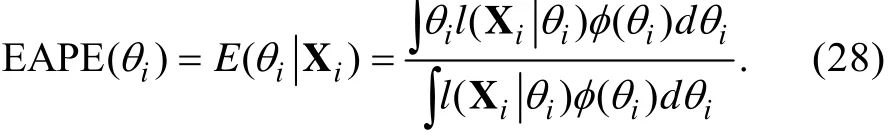

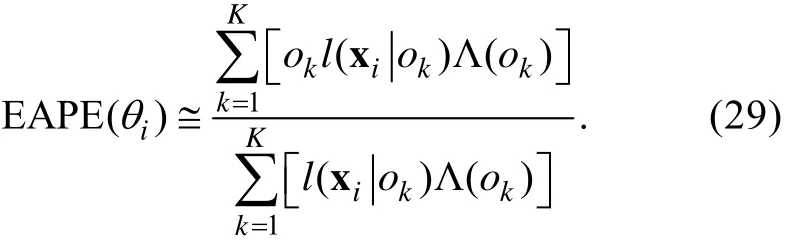
3 模拟研究
为了探明WMLE的具体表现, 本次模拟通过设定不同的考试条件, 对WMLE、MLE和EAPE的偏度(bias)和返真性能进行比较研究, 并对相关影响因素进行分析。
3.1 模拟设计
不失一般性, 在这次模拟中,θ
的真值取定为从−3.0到3.0以0.5为步长的间隔点, 共计13个不同的能力值。测验长度n
和项目区分度参数a
是θ
估计的主要影响因素, 为了考查它们的影响,n
取定3个水平, 15, 30和50,a
也取定3个水平, 0.5, 1.0和2.0, 交叉组合共生成9种测试条件. 每种测试条件下, 除a
以外, 其它项目参数真值的选取方式如下: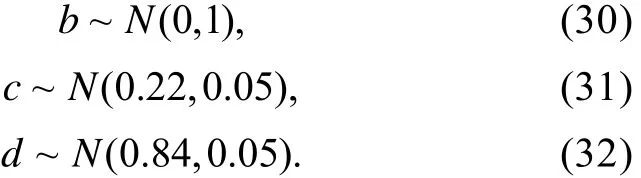
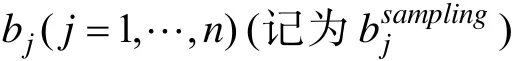


θ
值随机抽取测试反应向量1000组。然后, 计算每组反应数据对应的WMLE(θ
)、MLE(θ
)和EAPE(θ
). 需要强调的是, 如果随机抽取了全是0或全是1的反应向量, 应予以删除, 进行重新抽取。这样做的目的是为了使似然方程有解,即MLE(θ
)存在。最后, 为了比较3种估计方法的偏差和返真性能, 需要计算以下3种指标:平均偏差(mean error, ME)、绝对平均偏差(absolutemean error, ABME)和均方根误差(rootmean squared error, RMSE ),
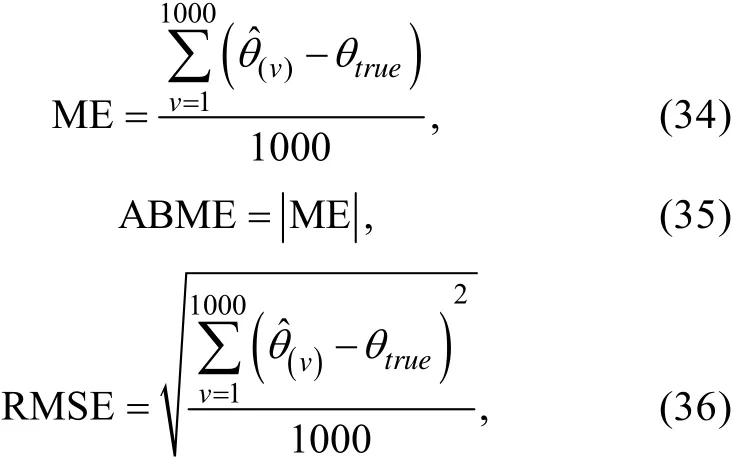

3.2 模拟结果
3.2.1 WMLE、MLE和EAPE的偏差比较
图1和图2展示了9种测验条件下WMLE ()θ
,MLE()θ
和EAPE()θ
的ME和ABME随θ
的变化曲线。经仔细观察, 可以发现以下现象:(1)如图1所示, WMLE()θ
和EAPE(θ
)的ME具有相同的变化趋势, 当θ
小于0.0(测试中心)时,它们的ME趋于正的, 即估计值比真值偏大; 当θ
大于0.0时, 它们的ME趋于负的, 即估计值比真值偏小。MLE()θ
的ME表现出恰恰相反的变化趋势,0.0左侧的θ
值对应的ME趋于负的, 0.0右侧的θ
值对应的ME趋于正的。3种估计ME的变化趋势与已有研究相吻合(Warm, 1989; Penfield & Bergeron,2005), 符合它们偏差的变化特点。(2)如图2所示, 每种测试条件下, WMLE()θ
的ABME都是3种估计中最小的, 其次是MLE(θ
),EAPE()θ
的ABME最大。这说明WMLE()θ
的偏差最小(无偏性最佳), MLE()θ
的偏差其次(无偏性居中), EAPE()θ
的偏差最大(无偏性最差)。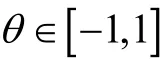
m
或a
的增加, 3种估计的ABME均表现出减小的趋势, 并且它们的差异也随之减小。例如, 当a
=2.0,m
=50时, 3种估计的ABME均是9种测试条件下最小的, 并且3种估计ABME的差异也是最小的。此外,m
和a
对MLE(θ
)和EAPE (θ
)的ABME影响非常显著, 而对WMLE(θ
)的ABME影响微乎其微。甚至在m
和a
均较小的情况下, 例如, 当a
=0.5,m
=15时, WMLE(θ
)也没有表现出较大的偏差。这说明, 相比于其它两种估计方法,WMLE的无偏性受实际情况影响较小, 保持了很高的稳定性。3.2.2 WMLE、MLE和EAPE的返真性能比较
图3展示的是, 9种测试条件下, 3种估计的RMSE随θ
的变化曲线. 经仔细观察, 可以发现:
θ
)的RMSE随θ
的变化比较稳定,即使对于极大或极小的θ
值, 它的RMSE也没有出现很大幅度的增加, 当m
较大时, 它的RMSE曲线要更加平稳。这说明对于大多数θ
值, WMLE(θ
)都表现出优良的返真性能, 这对4PL模型的实际应用非常有意义。EAPE(θ
)的RMSE随θ
的变化也较为稳定, 只是在m
=15的条件下, 它的RMSE变化较为显著。相比之下, MLE()θ
的RMSE随θ
的变化最为剧烈, 随着θ
远离0.0, MLE()θ
的RMSE明显增大, 返真性能明显降低。
图1 九种测试条件下, WMLE、MLE和EAPE的ME变化曲线

图2 九种测试条件下, WMLE、MLE和EAPE的ABME变化曲线

图3 九种测试条件下, WMLE、MLE和EAPE的RMSE变化曲线
(3)随着m
的增大, WMLE()θ
、MLE()θ
和EAPE()θ
的RMSE均表现出显著减小的趋势, 而且它们之间的差异也随之减小。随着a
的增加,EAPE()θ
和WMLE()θ
的RMSE表现为减小的趋势,但MLE()θ
的RMSE的变化跟θ
的取值范围有关。当θ
在测试中心附近时, MLE()θ
的RMSE随的增加而减小, 否则, 随a
的增加而增大。线性测试的特点、a
对测试信息量的影响以及MLE的大样本性质,是导致这一现象的原因。根据MLE的大样本性质可知, MLE()θ
的精度完全由测试的信息量决定,在线性测试中,a
越大, 距离测试中心较近的θ
值的测试信息量越大, 而距离测试中心较远的θ
值的测试信息量越小。所以, 随着a
的不同, MLE()θ
的RMSE表现出上述变化趋势是符合MLE的性质的。(4)与偏差的表现类似, 随着测试情况的变化,WMLE()θ
的返真性能表现出较高的稳定性, 受测试条件的影响很小, 另外两种估计方法的返真性能的稳定性相对较差, 易受考试实际情况影响。从实际应用的角度看, 方法性质的稳定性很重要, 性质稳定的方法意味着更加安全, 所以应更受青睐。4 结论与展望
本文基于Warm的加权极大似然估计理论提出了适用于4PL模型潜在特质参数的WMLE。理论上, WMLE能够保持较高的精度并降低潜在特质参数估计的偏差, 这对IRT模型的应用具有重要的意义。模拟研究的结果表明:与MLE和EAPE相比,WMLE表现出更加优良的统计性质。首先, WMLE的偏差要明显小于MLE和EAPE; 其次, WMLE具有良好的返真性能, 保证估计具有较高的精度; 最后, WMLE的性质(偏差和返真性能)对测试长度和项目区分度的变化表现出良好的稳定性, 即使在测试长度较短或项目区分度较低的情况下, WMLE的性质依然良好。相比之下, MLE和EAPE的稳定性就要差一些, 测试长度对MLE有很大的决定作用,而项目区分度对EAPE的影响比较显著。因此, 当测试的项目不多时, 不宜选用MLE, 当测试项目的区分度不高时, 需谨慎考虑选用EAPE。
在形式上, WMLE与MAPE完全一样, 但WMLE并不要求权函数f
(θ
)是概率密度函数, 所以WMLE与MAPE在理论上存在本质的不同。近年来, Magis等一批学者对WMLE与MAPE的关系进行了深入研究, 取得了一些重要结果。Warm (1989)证明了2PL模型的WMLE与Jeffreys先验下的MAPE (简称JMAPE)存在等价关系, 这一结论具有较高的学术价值, 也引起了人们的关注。Magis (2015)证明:在GPCM下这种等价关系依然成立。不过, Magis和Raiche (2012)的研究表明, 3PL模型的WMLE与JMAPE的等价关系不成立, 同水平θ
的WMLE值要比JMAPE值稍大一些。3PL模型的WMLE是否与其它先验下的MAPE存在等价关系, Magis的研究并未提及。4PL模型潜在特质参数的WMLE与MAPE是何关系, 能否与某种先验下的MAPE等价,是值得我们进一步深入研究的问题。因为该问题比较复杂, 仅仅通过模拟比较难以得到一般性的结论,所以本文没有对WMLE与MAPE的性质进行比较。此外, 本次模拟研究是在线性测试的环境下进行的, 所得结论不能简单的推广到CAT。根据CAT的设计原理, 每个被试所作答的试卷都是为其“量身定做”的, 保证了测试中心与被试潜在特质水平的距离最小。由图3可知, 当被试的潜在特质水平与测试中心非常接近时, EAPE表现出最好的返真性能。可见, 在CAT的环境下, 4PL模型的WMLE未必能具有与本研究类似的优良性, 很有可能EAPE具有最佳效果。但这仅仅是一种预想, 具体情况有待被进一步深入研究。
Baker, F. B., & Kim, S. H. (2004).Item response theory:Parameter estimation techniques
. New York: Marcel Dekker.Barton, M. A., & Lord, F. M. (1981). An upper asymptote for the three-parameter logistic item response model. InResearch Bulletin
(pp. 81–20).
Princeton, NJ: Educational Testing Service.Green, B. F. (2011). A comment on early student blunders on computer-based adaptive tests.Applied Psychological Measurement, 35
, 165–174.Liao, W. W., Ho, R. G., Yen, Y. C., & Cheng, H. C. (2012). The four-parameter logistic item response theory model as a robust method of estimating ability despite aberrant responses.Social Behavior and Personality, 40
, 1679–1694.Linacre, J. M. (2004). Discrimination, guessing and carelessness asymptotes: Estimating IRT parameters with Rasch.Rasch Measurement Transactions, 18
, 959–960.Loken, E., & Rulison, K. L. (2010). Estimation of a fourparameter item response theory model.British Journal of Mathematical and Statistical Psychology, 63
, 509–525.Magis, D. A. (2013). Note on the item information function of the four-parameter logistic model.Applied Psychological Measurement, 37
, 304–315.Magis, D. A. (2014). Accuracy of asymptotic standard errors of the maximum and weighted likelihood estimators of proficiency levels with short tests.Applied Psychological Measurement, 38
, 105–121.Magis, D. A. (2015). A note on weighted likelihood and Jeffreys modal estimation of proficiency levels in polytomous item response models.Psychometrika, 80
, 200–204.Magis, D. A., & Raiche, G. (2012). On the relationships between Jeffreys modal and weighted likelihood estimation of ability under logistic IRT models.Psychometrika, 77
, 163–169.Mathilda, D. T. (2003).IRT from SSI: BILOG-MG, MULTILOG,PARSCALE, TESTFACT
. Chicago, IL: Scientific Software International.Osgood, D. W., McMorris, B. J., & Potenza, M. T. (2002).Analyzing multiple-item measures of crime and deviance I:Item response theory scaling.Journal of Quantitative Criminology, 18
, 267–296.Penfield, R. D., & Bergeron, J. M. (2005). Applying a weighted maximum likelihood latent trait estimator to the generalized partial credit model.Applied Psychological Measurement, 29
, 218–233.Qi, S. Q., Dai, H. Q., & Ding, S. L. (2002).Principles of modern educational and psychological measurement
. Beijing: Higher Education Press.[漆书青, 戴海琦, 丁树良. (2002).现代教育和心理测量学原理
. 北京: 高等教育出版社.]Rulison, K. L., & Loken, E. (2009). I’ve fallen and I can’t get up: Can high ability students recover from early mistakes in computerized adaptive testing?.Applied Psychological Measurement, 33
, 83–101.Rupp, A. A. (2003). Item response modeling with BILOG-MG and MULTILOG for Windows.International Journal of Testing, 3
, 365–384.Tavares, H. R., de Andrade, D. F., & Pereira, C. A. (2004).Detection of determinant genes and diagnostic via item response theory.Genetics and Molecular Biology, 27
, 679–685.Waller, N. G., & Reise, S. P. (2009). Measuring psychopathology with non-standard IRT models: Fitting the four parameter model to the MMPI. In S. Embretson& J. S. Roberts (Eds.),New directions in psychological measurement with modelbased approaches
(pp. 147–173). Washington, DC: American Psychological Association.Wang, S. D., & Wang, T. Y. (2001). Precision of Warm’s weighted likelihood estimates for a polytomous model in computerized adaptive testing.Applied Psychological Measurement, 25
, 317–331.Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory.Psychometrika, 54
, 427–450.Yen, Y. C., Ho, R. G., Liao, W. W., Chen, L. J., & Kuo, C. C.(2012). An empirical evaluation of the slip correction in the four parameter logistic models with computerized adaptive testing.Applied Psychological Measurement, 36
, 75–87.附录
定理
:对于4PL模型(1), 有以下等式成立,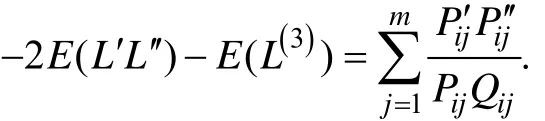
证明
:根据方程(6)和(7)有,

