非色散非线性Schrödinger方程的暗孤子解

丁国华， 苏　婷，方建印，王　辉

(1.河南工程学院 图书馆，河南 郑州 451191; 2.河南工程学院 理学院，河南 郑州 451191)



非色散非线性Schrödinger方程的暗孤子解

丁国华1， 苏婷2，方建印2，王辉2

(1.河南工程学院 图书馆，河南 郑州 451191; 2.河南工程学院 理学院，河南 郑州 451191)

摘要：非色散非线性Schrödinger方程和它的Lax对被显示给出.借助于谱问题之间的规范变换，孤子解的达布变换得以构造，作为应用给了出非色散非线性Schrödinger方程的显示解.

关键词：达布变换；暗孤子解；非线性Schrödinger方程

对孤子方程求显示解是物理学和数学领域都很感兴趣的话题.近年来已经有许多求解的方法，如反散射方法[1-2]、双线性(Hirota)方法[3]、达布变换法[4-6]、代数几何方法[7]、穿衣方法[8]等，这些方法各有特点，其中达布变换方法是从平凡解出发得到孤子方程的精确解.本研究利用达布变换方法求非色散非线性Schrödinger方程的单孤子解和二孤子解.

iqt+qxx-2|q|2q=0

(1)

许多学者对方程(1)都有深入的研究，Andrew在文献[9]中借助Crum Transformation给出了方程(1)的有理解.Ruiyu等在文献[10]中给出了方程(1)的显示解.

1非色散非线性Schrödinger方程的达布变换给出方程(1)保谱问题

φx=Uφ, U=iλσ3+Q，

(2)

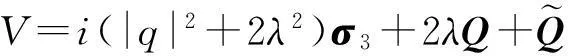
(3)

由相容条件Ut-Vx+[U,V]=0可以得到非色散非线性Schrödinger方程(1).

首先，引入谱问题(2)和(3)的规范变换

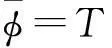
(4)

其中，T由以下两式决定：

(5)

(6)

更进一步，式(2)和式(3)转化为

(7)

(8)

设φ(λj)=(φ1(λj),φ2(λj))T和ψ(λj)=(ψ1(λj),ψ2(ψj))T是式(2)和式(3)的两个基本解.由式(4)可知存在常数rj满足

(Aφ1(λj)+Bφ2(λj))-rj(Aψ1(λj)+Bψ2(λj))=0，(Cφ1(λj)+Dφ2(λj))-rj(Cψ1(λj)+Dψ2(λj))=0.

(9)

式(9)也可以写成线性系统

A+σjB=0,C+σjD=0,

即

(10)

其中,

(11)

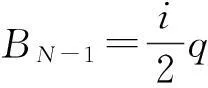
从式(9)可知，detT(λ)是λ的2N-1次多项式,且detT(λj)=α2[A(λj)D(λj)-B(λj)C(λj)].另一方面，由式(10)可知

A(λj)=-σjB(λj),C(λj)=-σjD(λj),

(12)

(13)

这表明λj(1≤j≤2N-1)是detT的根.

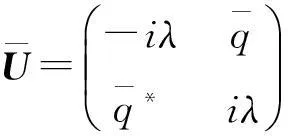
下列变换

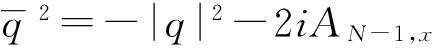
(14)

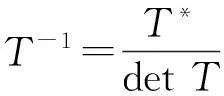
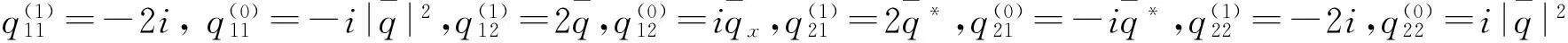
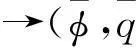
2多孤子解

利用前面的达布变换可以得到孤子方程(1)的一系列的精确解.取平凡解q=0，代入Lax对(2)和(3)中，得到其基本解.选取两个基本解为

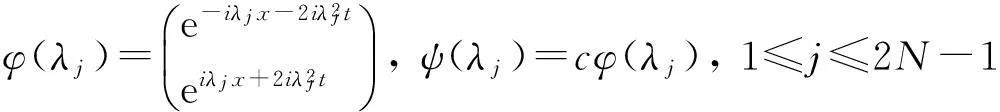
由等式(11)可知,

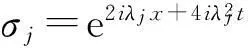
(15)

利用线性系统(10)和条件(14)，借助克莱姆法则求解，得到

(16)

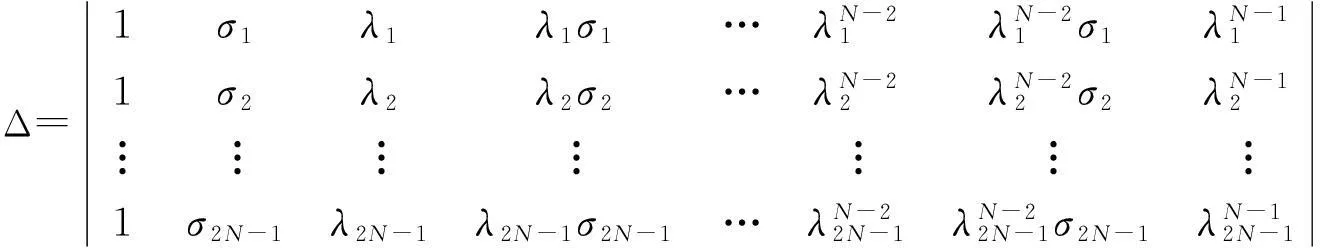
(17)

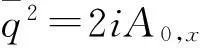
由式(15)可知，只需取λj(j=1,2,3)不同的值，即可以得到非色散非线性Schrödinger方程的解.

参考文献：

[1]ABLOWITZMJ，SEGURH.SolitonsandtheInverseScatteringTransform[M].Philadelphia:SIAM,1981.

[2]NEWELLAC.SolitonsinMathematicsandPhysics[M].Philadelphia:SIAM，1985.

[3]HIROTAR.DirectMethodsinSoliotnTheory[M].Berlin:Springer-Verlag,2004.

[4]MATVEEVVB,SALLEMA.DarbouxTransformationandSolitons[M].Berlin:Springer-Verlag,1991.

[5]GENGXG,TAMHW.DarbouxtransformationandsolutionsforgeneralizednonlinearSchrödingerequations[J].JouralofMathematicalPhysics,1999(40)：3948-3955.

[6]FANEG.Darbouxtransformationandsoliton-likesolutionfortheGerdjikov-Ivanovequation[J].JournalofPhysicsA:MathematicalandGeneral,2000(33)：6925-6933.

[7]GENGXG,CAOCW.DarbouxtransformationandsolitonsolutionsforgeneralizednonlinearSchrödingerequations[J].JapaneseJournalofAppliedPhysics,1999(68)：289-299.

[8]DAIHH,JEFFREYA.Theinversescatteringtransformsforcertaintypesofvariable-coefficientKdvequations[J].PhysicsLettersA,1989(139)：369-372.

[9]ANDREWNW.Scale-space:anewapproachtomulti-scaledescription[J].JournalofPhysicsA:MathematicalandGeneral,1997(30)：7473-7483.

[10]RUIYUH.AnewapproachtoexactsolitonsolutionsandsolitoninteractionforthenonlinearSchrödingerequationwithvariable-coefficient[J].OpticsCommunications,2004(236)：79-86.

The dark soliton solution of the nondispersive nonlinear Schrödinger equation

DING Guohua1, SU Ting2，FANG Jianyin2，WANG Hui2

(1.Library,HenanInstituteofEngineering,Zhengzhou451191,China;

2.CollegeofSciences,HenanInstituteofEngineering,Zhengzhou451191,China)

Abstract:The nondispersive nonlinear Schrödinger equation and its Lax pair are given explicitly. With the help of gauge transformation between spectrum problems, the Darboux transformation of soliton solution is constructed. As an application, the explicit solutions of the nondispersive nonlinear Schrödinger equation are derived.

Key words:Darboux transformation；dark soliton solution；nonlinear Schrödinger equation

作者简介：丁国华(1977-)，男，河南周口人，助教，主要从事孤立子与可积系统研究.

基金项目：国家自然科学基金项目(11301149)；河南省基础前沿项目(132300410310，102300410212)

收稿日期：2015-08-03

中图分类号：O322

文献标志码：A

文章编号：1674-330X(2015)04-0077-04