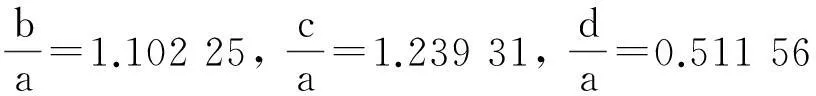双曲柄机构的杆长参数方程及应用
2016-01-31李家伟
李家伟
(武昌工学院 机械工程学院,湖北 武汉 430065)
双曲柄机构的杆长参数方程及应用
李家伟
(武昌工学院 机械工程学院,湖北 武汉 430065)
摘要:根据按照急转速度系数设计双曲柄机构的现状,提出了按照急转速度系数设计双曲柄机构的参数设计法.通过几何分析推导,完成了双曲柄机构分类型及杆长参数方程,设计实例叙述了双曲柄机构的杆长参数方程及应用.
关键词:双曲柄机构;参数方程;应用
双曲柄机构是铰链四杆机构最常见的形式之一,它可以将主动曲柄的等速回转运动变换成从动曲柄的变速回转运动,与其他机构串联可以满足执行构件不同的输出特性,如惯性筛、刨床和插床工作行程的匀速运动及回程的快返运动等.
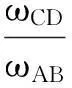
在图1的ABCD和AB1C1D中,用解析法求得[3-4]:

图1 双曲柄机构急转速度示意图Fig.1 Schematic diagram of double crank mechanism whirling speed
(1)

(2)
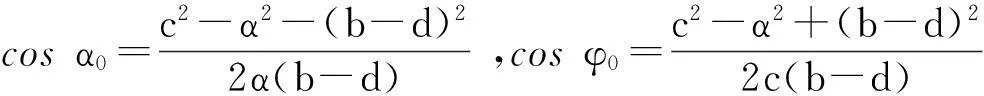
式(1)和式(2)分别是满足急转速度系数K的方程,也是按急转速度系数K设计双曲柄机构必须满足的方程,称为基本方程.利用基本方程,一方面对现有机构进行急转速度系数的分析[5];另一方面,联立其他辅助方程求得机构的尺寸.按急转速度系数K设计双曲柄机构有两种方法,一种方法是先按急回转速度系数和传动角设计曲柄摇杆机构,再倒置成双曲柄机构,这种方法可满足双曲柄机构传动角的要求,但不满足双曲柄机构的急转速度系数,因为曲柄摇杆机构的急回转速度系数不同于倒置后双曲柄机构的急转速度系数,极易使读者认为是按急转速度系数K设计双曲柄机构的[6].另一种方法是在满足传动角的条件下,证明急转速度系数K是从动曲柄尺寸c的单减函数,用迭代法求解满足K的从动曲柄尺寸c,进而计算机构的其他尺寸.这种方法实际上是一种试凑方法,计算量大且只适合于传动角类的附加条件.运用文献[7]和文献[8]的方法,通过建立式(1)和式(2)的杆长参数方程,给定或结合附加条件确定参数,再用杆长参数方程计算机构尺寸,以达到简化设计计算的目的.
1杆长参数方程
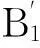
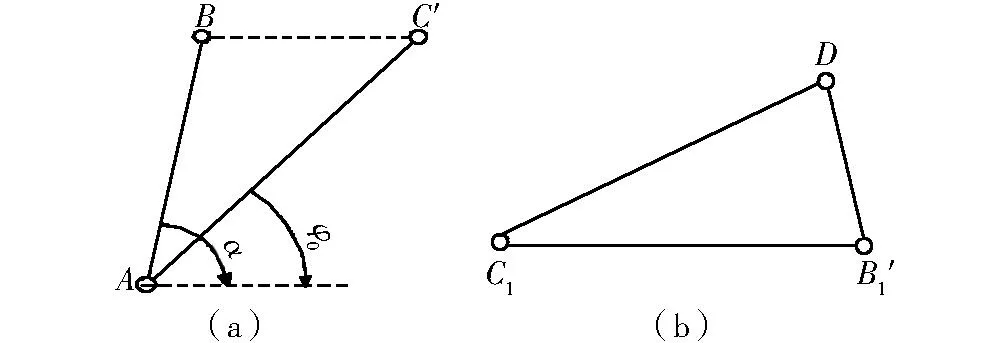
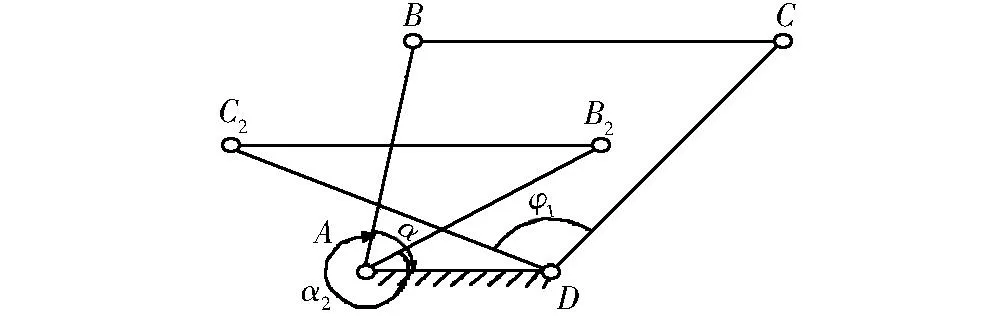
图2 双曲柄机构急转速度分析Fig.2 Schematic diagram of double crank mechanism whirling velocity analysis
由图2(a)可知,使三角形成立的条件为b-d b (3) a+d (4) c+d (5) 同理,由图2(b)得 b+d (6) a (7) c (8) 由于d是最短杆且为机架,由式(4)、(5)、(6)可知满足杆长条件.式(3)、(7)、(8)分别是以b,a,c为最长杆的装配条件.因此,图1和图2(b)的三角形成立是图1双曲柄机构ABCD存在的充分条件. (9) (10) (11) (12) (13) (14) 由式(10)和式(13)得 (15) 由式(11)和式(14)联立求解,得 (16) (17) 式(10)、(16)、(17)是用α0和φ0两参数描述的双曲柄机构的杆长参数方程,也是基本方程(1)和(2)的参数方程,式(15)是参数α0和φ0的约束方程.在已知α和φ的条件下,选取或按其他附加条件(传动角或杆长比等)确定满足式(15)的α0和φ0,利用杆长参数方程就可以设计出符合急转速度系数K的双曲柄机构. 2双曲柄机构类型与杆长参数方程 双曲柄机构在两曲柄的角速度相等时,按连杆B1C1和BC位置的不同可分为A型、B型和C型. 如图1所示,连杆两位置分别在第一、二象限和第三、四象限,这种类型称为A型.判别式为π<φ0+φ<2π, φ0+φ<α0+α<2π, 这时0<(α0+α)-(φ0+φ)<π满足式(12),杆长方程(10)、(15)、(16)、(17)自然适用.B型和C型双曲柄机构示意图分别见图3和图4. 图3 B型双曲柄机构Fig.3 Double crank mechanism type B 图4 C型双曲柄机构Fig.4 Double crank mechanism type C 如图4所示,连杆BC和B1C1位置分别在第一、二象限和坐标轴上,这种类型称为C型.判别式为α0+α=2π, φ0+φ=π,这时(α0+α)-(φ0+φ)=π, 式(12)~(17)不适用.由图3得 a+c-d=b. (18) 式(18)、式(10)和式(11)联立求解,并将α0+α=2π, φ0+φ=π代入,得 (19) 3杆长参数方程应用及实例 (2)α0和φ0的确定.机构的相对尺寸有3个,加上α0和φ0共5个未知数,杆长方程(10)、(16)、(17)和约束方程(15)共4个,有一个未知数待定.在α和φ确定的条件下,选择φ0∈(0,π),再由方程(15)确定α0∈(φ0,π),或将杆长方程表达辅助条件再与方程(15)联立求解α0和φ0. (3)类型的确定.若π<φ0+φ<2π, φ0+φ<α0+α<2π, 则为A型;若2π<α0+α<2π+φ0, φ0<φ0+φ<π, 则为B型;若π<α<2π, 可选C型. (4)尺寸计算.若为A或B型,由式(10)、(16)、(17)得 (20) 若是C型,由式(19)得 (21) 按急转速度系数K=2.8(或φ=120°, α=210°)设计双曲柄机构. 解 (1)选择φ0=90°,由式(15)得 α0=126.206 02°; 参考文献: [1]杨增选,高虹霓,田野.双曲柄机构的急回运动特性研究[J].空军工程大学学报:自然科学版,2002(5):83-85. [2]孙桓,陈作模,葛文杰.机械原理[M].7版.北京:高等教育出版社,2006. [3]韩继光,王贵成.按速度变化系数设计双曲柄机构[J].机械设计与研究,2004(12):34-35. [4]王丹.按行程速比系数K综合双曲柄机构[J].华东交通大学学报,2000(6):88-91. [5]李宏,张全明,洪琦.双曲柄机构急回运动分析[J].机械设计与研究,2001(12):41-43. [6]刘远伟,常勇,李延平.按行程速比系数K设计平面双曲柄机构的解析方法[J].机械科学与技术,1998(2):179-181. [7]程友联,吴晓红.曲柄摇杆机构的参数设计法[J].机械设计,2010(9):60-62,96. [8]程友联,汤柳明.曲柄摇杆机构的参数方程及应用[J].武汉交通科技大学学报,2000(3):317-319. [9]高广娣,朱荣光,毕新胜,等.双曲柄机构输出不均衡运动特性与杆长间的相关性研究[J].机械传动,2013(6):26-27,41. Rod length parameter equation of double-crank mechanism and its applications LI Jiawei (CollegeofMechanics,WuchangInstituteofTechnology,Wuhan430065,China) Abstract:This paper briefly describes the current situation of designing double-crank mechanism with racing velocity coefficient and puts forward a parameter design method of designing double-crank mechanism with racing velocity coefficient. It completes the division of the types and club length parameter equation of double-crank mechanism by means of geometric analysis and derivation. It also describes the application of club length parameter equation of double-crank mechanism with the help of design examples. Key words:double-crank mechanism; parameter equation; application 作者简介:李家伟(1964-),男,湖北武汉人,副教授,研究方向为机械设计理论与方法. 基金项目:湖北省教育科学“十二五”规划重点课题(2014A047) 收稿日期:2015-05-25 中图分类号:TH112 文献标志码:A 文章编号:1674-330X(2015)02-0044-04



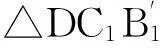
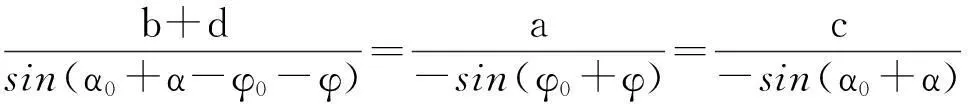


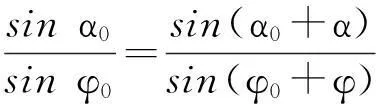
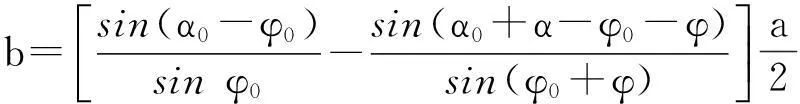
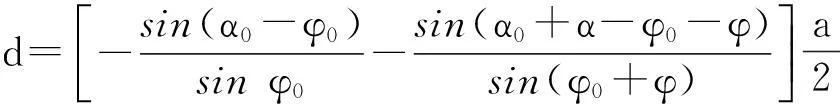

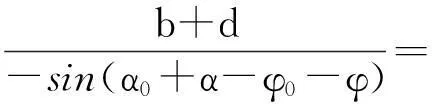
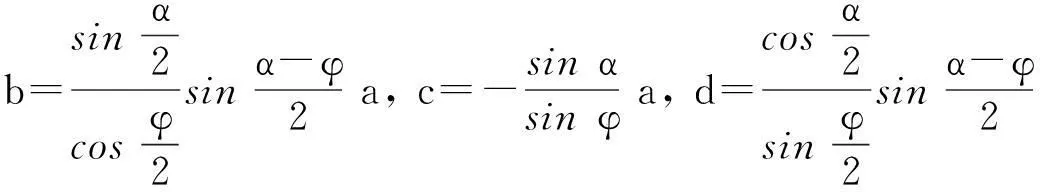
3.1 应用说明及步骤


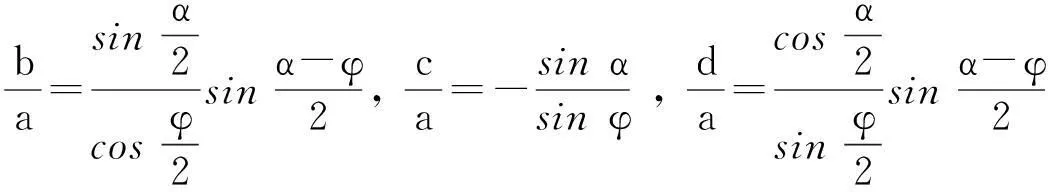
3.2 设计实例