梯度神经网络在p次方根求解中的应用

肖　林,皮赛男,孟凡斌

(吉首大学信息科学与工程学院，湖南 吉首 416000)



梯度神经网络在p次方根求解中的应用

肖林,皮赛男,孟凡斌

(吉首大学信息科学与工程学院，湖南 吉首 416000)

摘要：设计了一个针对一般问题求解的梯度神经网络模型.为了求解p次方根,定义一个基于平方的标量取值的能量函数，再根据梯度下降法,进一步推导出求解p次方根的梯度神经网络模型.使用Matlab仿真软件进行建模、仿真和验证，计算机仿真结果证实了梯度神经网络实时求解p次方根的有效性.

关键词：梯度神经网络；p次方根；Matlab仿真

梯度神经网络是由若干个非线性神经元构成的全连接型的人工神经网络，其中任何一个神经元既接收来自于其他神经元的输入，同时也对其他神经元输出信号[1].递归神经网络构成的是具有反馈的系统，输出可以返回来调节输入，从而建立动态关系.因此，也可将递归神经网络看作是以权值和外部输入为参数的、关于内部状态的一个动力学系统[2].当前，梯度神经网络因具有平行分布特性、自适应和自学习等能力，已成为许多学科十分活跃的研究话题，并在联想记忆、优化计算、鲁棒控制、模式识别、机械臂运动控制、故障诊断等领域得到广泛应用[3-4].

求解p次方根是求解等式问题中的一个重要情况[5]，应用在各种科学与工程领域中.通过求解p次方根，一幅图可以在Torelli群中被描述出来，再如Harris图像可以从其原图像的p次方根中提炼得到[5].因此，很多的数值算法被提出来求解这样一类p次方根问题.在对神经网络深入研究的基础上，许多基于神经动力学的模拟求解器也被广泛提出来.考虑到潜在的大规模电路实现和高性能并行处理能力，神经动力学方法已经被认为是一种强有力的实时问题求解方法.

1梯度神经网络设计

作为进一步讨论的基础，将针对标量取值的一般等式问题，设计一个可以普遍应用的梯度神经网络.

1.1 问题描述

考虑如下标量取值的一般等式问题：

f(x)=0，

(1)

其中f(·)代表一个映射函数，它既可以为线性函数，也可以为非线性函数.接下来，就等式问题(1),设计一个梯度神经网络，该梯度神经网络可以实时求解一个x(t)∈R,它能满足一般方程(1)的要求.

1.2 梯度神经网络模型

在这一节,将根据梯度神经网络设计方法，开发一般的梯度神经网络模型来实时求解一般等式问题(1).

首先,为了监控等式(1)的求解过程,利用梯度设计方法,可以定义一个基于平方的标准取值的能量函数:

(2)

显然,当该能量函数等于0时,所对应的解x可以满足一般等式问题(1)的要求.

其次,为了使该能量函数(2)能够收敛到0,可以使该能量函数沿着它的负梯度方向下降,所以能量函数(2)的负梯度可以求得如下:

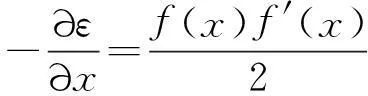
最后,基于一个典型的负梯度信息的连续时间自适应法则，可以推导出如下普遍适应的梯度神经网络模型:

(3)

其中神经状态x(t)从随机产生的初始值x(0)出发.对应于一般等式方程(1)的解,设计参数λ>0用来调节一般梯度神经网络模型(3)的收敛速度.

2梯度神经网络在p次方根求解中的应用

如上文所提到的,求解p次方根是求解等式问题中的一个重要情况，如通过求解p次方根，一幅图可以在Torelli群中被描述出来，再如Harris图像可以从其原图像的p次方根中提炼得到.所以,根据上一节一般梯度神经网络的设计过程，现将该设计方法具体应用到p次方根求解.

首先,考虑如下标量取值的p次方根问题:

xp(t)-a=0t∈[0,+∞)，

(4)

其中a∈R表示一个标量取值的实数.现主要工作就是设计一个梯度神经网络来实时求解一个x(t)∈R,它能满足以上p次方根方程(4)的要求.为了表示方便，令x*(t)∈R表示a∈R的p次方根的理论解.

根据以上一般梯度神经网络的设计过程，为了监控静态p次方根的求解过程，先定义如下的一个基于平方的标准取值的能量函数:

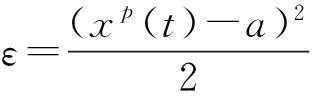
(5)

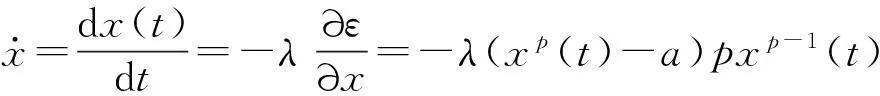
(6)

其中神经状态x(t)从随机产生的初始值x(0)出发.对应于p次方根方程(4)的解,设计参数λ>0用来调节一般梯度神经网络模型(6)的收敛速度.

3计算机仿真验证

为了验证梯度神经网络模型(6)的有效性,将挑选几个富有代表性的p次方根进行求解.

例1首先考虑如下的p次方根求解(具体来说p=4):

x4-16=0.

(7)

很显然,在实数域里面,方程(7)有2个理论解:一个是x*=2,另一个是x*=-2.下面将运用梯度神经网络模型(6)去实时求解p次方根方程(7).不失一般性,令设计参数λ=1,初始状态x(0)在[-5,5]区域内随机产生,仿真结果如图1，2所示.由图1可以看出,从[-5,5]区域内随机产生的初始状态出发,神经状态解在0.02 s内都收敛到p次方根的理论解x*=2或者x*=-2.这充分说明了梯度神经网络的有效性.神经状态解对应的误差函数收敛情况具体如图2所示.从图2可以得知，随着时间的推移,神经状态解对应的误差函数也在0.02 s内收敛到0,这更加直观地证明了梯度神经网络的有效性.

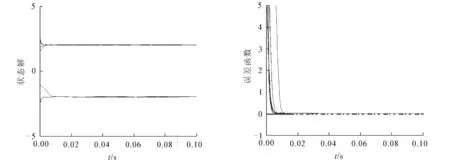
图1　梯度神经网络的状态解　　　　　　　　　　　　图2　对应的误差函数收敛情况

此外,为了说明设计参数λ的重要性,在其他条件不变的情况下,将设计参数λ调大为10.因神经状态的变化情况与图1类似,便不再展示,现只给出λ=10所对应的误差函数收敛情况.从图3可以看出,当λ=10,误差函数在2ms内就能收敛到0.如果再继续将λ调大为1 000,如图4所示,误差函数的收敛时间就只需要不到20μs.这仿真结果说明，设计参数λ对梯度神经网络的收敛速度有至关重要的作用.因此,在实际的应用中,应根据具体需求,选择一个合适的设计参数去设计梯度神经网络.

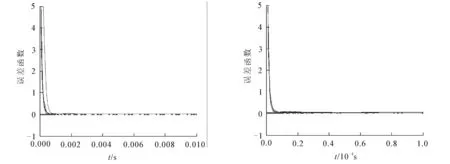
图3　λ=10时误差函数的收敛情况　　　　　　　　　　图4　λ=1 000时误差函数的收敛情况

在例1中,p次方根的理论解比较容易计算,但是有些p次方根的理论解是较难以计算出来的,所以为了再次验证梯度神经网络的有效性,下面来考虑一个更加复杂的p次方根.

例2考虑如下的p次方根求解：

x6+sin(5)-13=0.

(8)

显然,现无法手工计算该p次方根的理论解,因此将依据误差函数是否收敛到0来判断梯度神经网络是否收敛到p次方根方程(8)的理论解.在与例1相同的情况下,运用梯度神经网络来求解p次方根方程(8).图5显示了梯度神经网络求解该p次方根的误差函数收敛情况.从图5看到,误差函数在0.01s内就能收敛到0,这说明了梯度神经网络的有效性.图6给出了该误差函数所对应的状态解,在[-5,5]区域内的神经状态解都收敛到某一特定值.经Matlab软件核对,神经状态解都收敛到该p次方根方程(8)的理论解x*=1.55或者x*=-1.55.这一仿真实例再次证实了梯度神经网络的有效性.

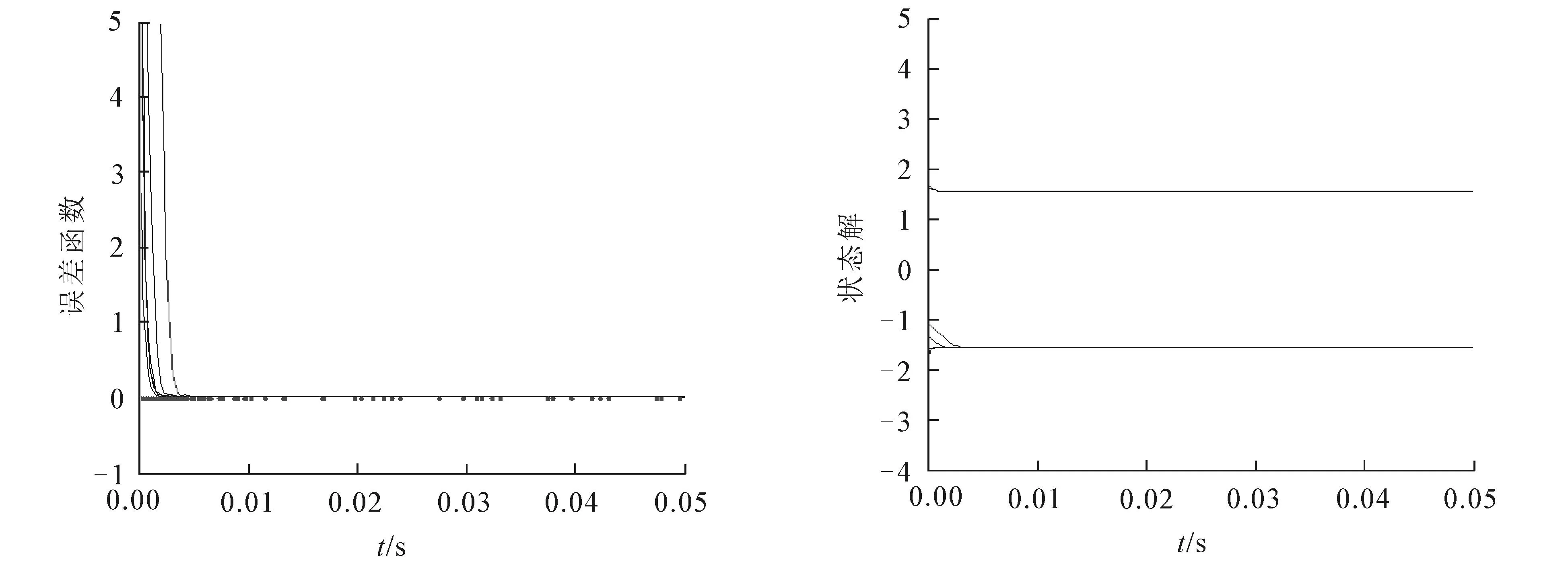
图5　梯度神经网络的误差函数收敛情况　　　　　　　　　　　图6　对应的状态解

4结语

提出一类求解p次方根的梯度神经网络,该神经网络的设计是基于一个标量取值的正能量函数.利用这个梯度神经网络进行计算机仿真,2个仿真实例都证实了梯度神经网络求解p次方根问题的有效性.通过选取不同的设计参数λ值,可以进一步加快梯度神经网络的收敛速度.

参考文献：

[1] 张雨浓,张禹珩,陈轲,等.线性矩阵方程的梯度法神经网络求解及其仿真验证[J].中山大学学报：自然科学版，2008,47(3):4 028-4 031.

[2] 马桂雨,王雪丹,万丹.基于遗传小波神经网络的变压器故障诊断[J].吉首大学学报：自然科学版，2013,34(1):51-56.

[3] 汤京永,时贞军.一类全局收敛的记忆梯度法及其线性收敛性[J].数学进展，2007,36(1):67-75.

[4] 赵凤遥,马震岳.基于递归小波神经网络的非线性动态系统仿真[J].系统仿真学报，2007,19(7):1 453-1 455.

[5]ZHANGYunong,XIAOLin,RUANGongqin,etal.ContinuousandDiscreteTimeZhangDynamicsforTime￣Varying4thRootFinding[J].NumericalAlgorithms,2011,57(1):35-51.

(责任编辑向阳洁)

Application of Gradient Neural Network to pth Root

XIAO Lin,PI Sainan,MENG Fanbin

(College of Information Science and Engineering,Jishou University,Jishou 416000,Hunan China)

Abstract:In this paper,a general gradient neural network is designed for solving the common problem.In order to find the pth root,a scalar￣valued square￣based energy function is defined.Then,according to the gradient descent method,a gradient￣neural￣network model is further derived for finding the pth root.Finally,the Matlab software is used for modeling,simulation,and verification.Computer￣simulation examples and their simulative results substantiate the effectiveness of the gradient neural network for finding the pth root.

Key words:gradient neural network;pth root;Matlab simulation

作者简介：肖林(1986—)，男，湖南邵阳人，吉首大学信息科学与工程学院讲师，博士，主要从事神经网络和机器人研究；孟凡斌(1964—)，男，湖南永顺人，吉首大学信息科学与工程学院副教授，主要从事电子电路和神经网络研究.

收稿日期：2014-12-01

中图分类号：TP183；O151.2

文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.03.004

文章编号：1007-2985(2015)03-0015-04