基于模糊数学的液压挖掘机故障诊断

舒　陵

(中冶集团铜锌集团公司资源开发有限公司，北京 100028)



基于模糊数学的液压挖掘机故障诊断

舒陵

(中冶集团铜锌集团公司资源开发有限公司，北京 100028)

摘要：为快速诊断出液压挖掘机产生的故障原因，构建了液压挖掘机故障诊断的模糊数学模型.通过经验数据隶属度矩阵和专家优序数隶属度矩阵计算出故障诊断原因向量，由最大隶属度原则得到最终故障原因.将此方法运用于SWE50型挖掘机液压系统故障中，顺利找出故障原因是液压泵磨损，泵油压力偏低.

关键词：液压挖掘机；故障诊断；模糊数学；隶属度矩阵

在众多大型工程机械设备中，液压挖掘机广泛运用于土石方工程施工.据统计，60%以上的土方工程量是由液压挖掘机完成的[1].因此，液压挖掘机的故障诊断尤为重要.作为一款复杂的机电一体化产品，液压挖掘机的故障类型繁多，产生原因复杂.多种征兆可由同一故障原因引起，同一故障征兆的产生原因也可以是多方面的，由此构成故障征兆与原因之间复杂的隶属关系[2-3].在液压挖掘机故障排除工作中，诊断故障所用时间约为70%，而维修的时间仅占30%[4]，所以，快速诊断液压挖掘机产生故障的原因是缩短其故障排除工作的重点.笔者将模糊数学理论及方法引入液压挖掘机故障诊断中，为液压挖掘机故障诊断提供新的思路与方法.

1模糊数学理论

1.1 隶属度函数

隶属度函数的确定方法主要包括模糊统计法和二元比较对比法.模糊统计法参考了概率统计的方法，对所考虑的几项指标进行论域的划分，相当于将论域U进行{A,A′}的划分，A′是A的余，每做一次实验，便对A进行一次划分.确定论域后，对所统计的数据形成调查表，然后根据调查表的内容建立频数分布表，再根据频数关系建立隶属度函数.二元比较对比法利用2个因素之间的影响程度比值关系确定排序，定量指标的排序与定性指标的排序一般分开进行，其中定性指标的排序需要先统一成定量指标再排序.

1.2 模糊集合

对论域上U上的模糊集合A，指定一个从U到[0,1]的映射为

μA:U→[0，1]，

u→μA(u∈[0，1]).

其中：μA就是A的隶属度函数；μA(u)为u对A的隶属度，当μA(u)=1时，u∈A;当μA(u)=0时，u∉A，当μA(u)仅取0,1这2个值时，隶属度函数μA退化为普通集合的特殊函数，A退化为普通集合.

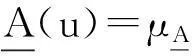
1.3 模糊关系

2故障模糊诊断模型

2.1 初始定义的建立

定义1假设某种故障发生时出现m种征兆，则第i种征兆的状态变量为xi(i=1,2,…,m)，故障征兆模糊向量为X={μx1(x1),μx2(x2),…,μxm(xm)}.

定义2设产生某类型故障的原因个数为n，则故障原因为yj(j=1,2,…,n)，故障原因模糊向量为Y={μy1(y1),μy2(y2),…,μyn(yn)}.

2.2 诊断矩阵的构造

隶属度的确立方法如下：

(1)由经验数据确定.

(1)

(2)初始隶属度值Sij由专家法确定.设某故障征兆xi由y1,y2,…,yn这n种原因引起，分析对比这n种原因，分析引起故障征兆xi的重要性，将最容易引起故障征兆的一种对比原因记一次优先序.设在所有相互对比中，原因yj的优先序数为tj，同时tk=max{tj|j=1,2,…,n}，则原因yj的故障征兆xi的初始隶属度为

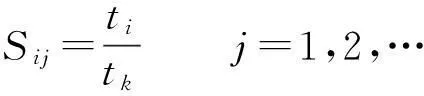
(2)

(3)设专家经验的权重为W1，经验数据权重为W2，且W1,W2≥0，W1+W2=1，则由W1和W2可得综合模糊隶属度为

rij=W1Sij+W2Viji=1,2,…，m;j=1,2,…,n.

(3)

2.3 故障的模糊诊断及分析

设故障征兆X=(x1,x2,…,xn)，故障原因Y=(y1,y2,…,yn)，则由模糊合成变换可得

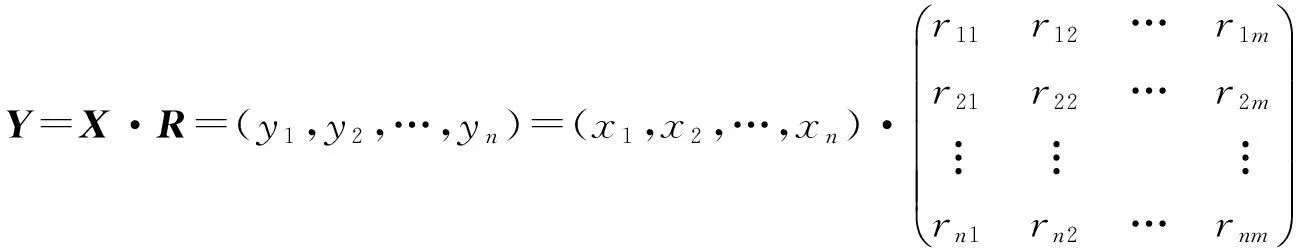
(4)

3故障诊断实例

以SWE50型挖掘机液压系统故障为例，采用模糊数学模型进行故障诊断.设液压系统故障征兆为xi，故障原因为yi，详见表1[7].

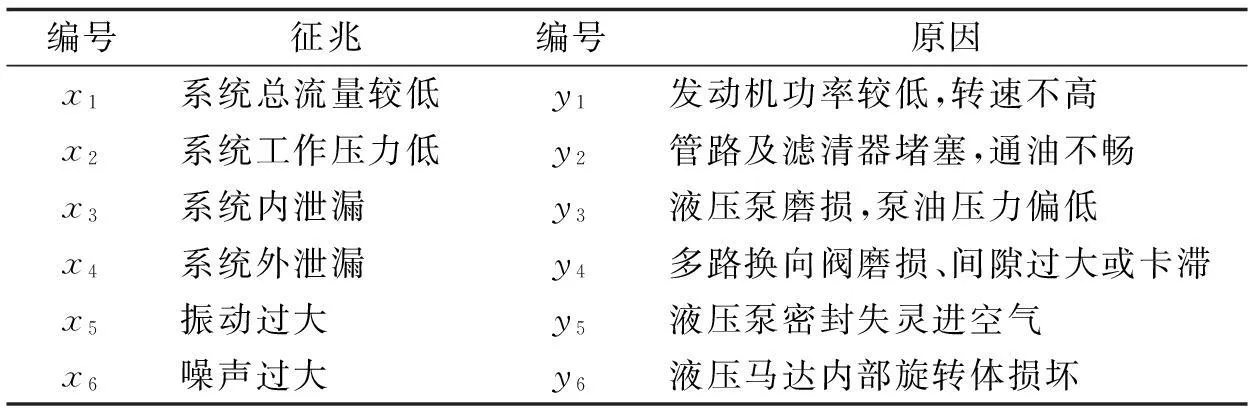
表1　故障征兆及其原因

根据以往排除SWE50型挖掘机液压系统故障经验，得出故障征兆隶属故障原因见表2.

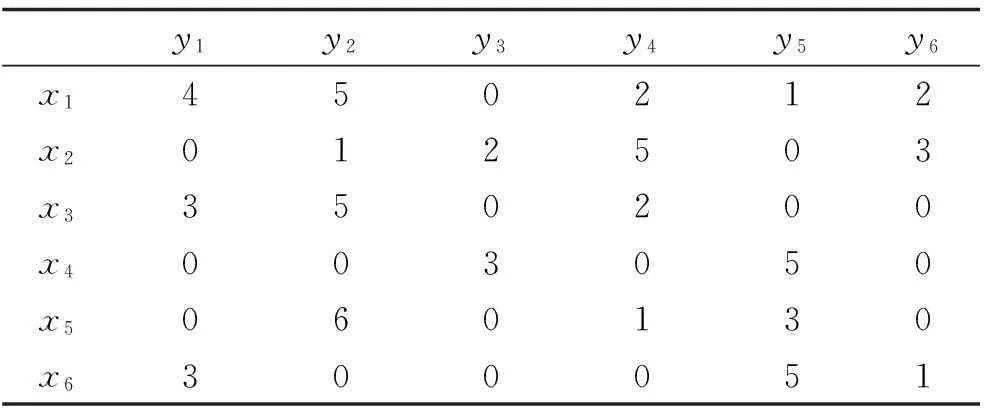
表2　挖掘机液压系统故障征兆隶属故障原因统计

将表3数据带入(1)式得经验数据诊断矩阵为

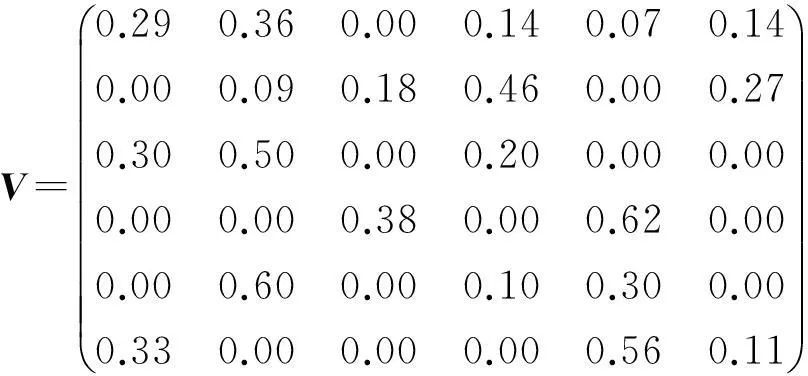
由(2)式得到初始隶属度值矩阵为

专家经验权重设为W1=0.6，经验数据权重设为W2=0.4，代入(3)式得到综合模糊隶属度矩阵为

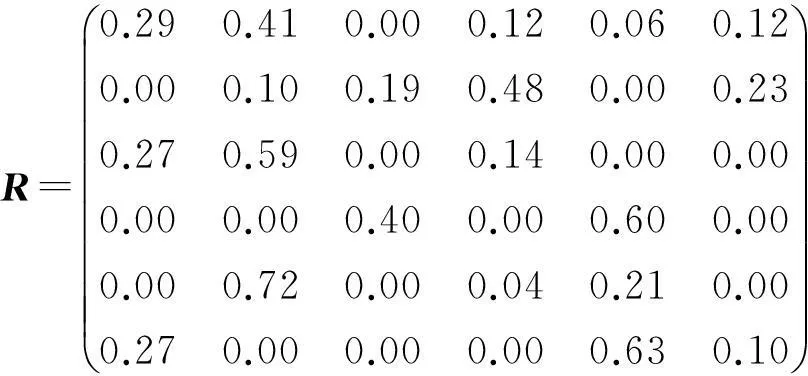
假设SWE50型挖掘机液压系统出现x4(系统外泄漏)，x5(振动过大)，x6(噪声过大)这3种故障征兆，则其故障征兆向量X=(000111).将X代入(4)式得诊断原因向量Y=(0.270.720.40

0.071.440.10)，由最大隶属度原则yt=max{yj|j=1,2,…,n}可得y5为故障原因.对照表1可知，故障诊断结果为液压泵磨损，泵油压力偏低.

4结语

针对液压挖掘机故障诊断，提出了基于模糊数学模型的故障诊断方法.通过经验数据隶属度矩阵和专家优序数隶属度矩阵计算得出故障诊断原因向量，由最大隶属度原则得到最终故障原因.该方法可以应用于其他工程机械的故障诊断，具有较为广阔的应用前景.

参考文献：

[1] 李孝明．中国小型液压挖掘机市场及其发展趋势和预测[J]．建设机械技术与管理，2006(7)：56-58.

[2] 钱锦武.液压挖掘机液压系统的故障分析与诊断[J].筑路机械与施工机械化，2007(6)：47-49.

[3] 张铁．液压挖掘机结构、原理及使用[M]．青岛：中国石油大学出版社，2002.

[4] 王庆海．液压挖掘机故障诊断系统的方案设计和推理方法研究[D]．杭州：浙江大学机械与能源学院，2002.

[5] 李安贵,张志宏,段凤英.模糊数学及其应用[M].北京：冶金工业出版社,1994.

[6] 莫智文,舒兰.模糊数学理论及其应用评述[J].四川师范大学学报:自然科学版,1998,21(3):330-335.

[7] 贺湘宇.挖掘机液压系统故障诊断方法研究[D].长沙：中南大学机电工程学院，2008.

(责任编辑陈炳权)

Fault Diagnosis of Hydraulic Excavator Based on Fuzzy Mathematics

SHU Ling

(Copper￣Zinc Resource Development Corporation,China Metallurgical Group Corporation,Beijing 100028,China)

Abstract:For rapid diagnosis of the fault cause of hydraulic excavator,this article,based on the fuzzy mathematical model,presents a new fault diagnosis method.This method first gets vector of fault diagnosis by means of the combination of membership degree matrix through experience data and the expert optimal ordinal membership degree matrix,and then uses the maximum membership degree principle to get the final cause of the problem.The fault cause of hydraulic excavator SWE50 (hydraulic pump wear and lower pump oil pressure) is successfully diagnosed by this method.

Key words:hydraulic excavator;fault diagnosis;fuzzy mathematics;membership matrix

作者简介：舒陵(1975—)，男，湖南长沙人，中冶集团铜锌集团公司资源开发有限公司工程师，主要从事钻机钻具等产品设计研究.

收稿日期：2015-03-10

中图分类号：TH137.7

文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.03.012

文章编号：1007-2985(2015)03-0052-04