对称非经典阻尼系统动力响应精确解算法比较

张　淼，　于　澜

(长春工程学院 理学院， 吉林 长春　130012)



对称非经典阻尼系统动力响应精确解算法比较

张淼，于澜

(长春工程学院 理学院， 吉林 长春130012)

摘要：分别采用频响函数法和复频率响应法对同一个数值算例进行了稳态响应、使用条件和范围以及误差来源分析，阐述了两种算法在工程执行过程中的特点及效率。

关键词：非经典阻尼系统； 动力响应； 频响函数矩阵； 标号现象

0引言

振型迭加法是动力分析中一种成熟且得到广泛应用的方法，尤其是对那些振型关于阻尼矩阵具有正交性的系统十分有效，这种系统称为经典阻尼系统，而当振型迭加法推广至非经典阻尼系统时，其计算响应的过程相当复杂[1]。但如果将在N维空间中描述的非经典阻尼系统转入2N维状态空间中描述，利用复模态构造状态向量，使用状态向量对角化状态矩阵来实现状态方程的解耦[2]，再把得到的响应解返至N维空间中，求得用复模态参数表达的非经典阻尼系统的响应解(解析解)的算法，一般称为复模态法或复频率响应法[3]。当然这种算法也可用于求解经典阻尼系统，但需使用实模态参数表达[4]。近年来，又有文献[5]提出了基于频响函数计算经典和非经典阻尼系统精确解的新方法，与振型迭加法只能求解经典阻尼系统、复频率响应法用实模态参数求解经典阻尼系统而用复模态参数求解非经典阻尼系统不同的是，这种新方法无论求解哪种阻尼系统的响应均使用的是实模态参数。

文中针对非经典阻尼动力系统，应用目前文献中已经出现的求解振动系统响应的解析解的两种算法进行详细分析和算例比较，来说明它们在编程实现过程中的使用条件、使用范围、误差来源和计算效率等，并指出利用模态参数求解响应的过程中可能出现的标号现象、重频现象及规范化常数的异常现象等。

1实模态参数与复模态参数

描述自由度为N的线性阻尼离散系统的自由振动方程为

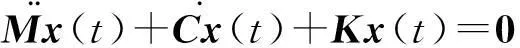
(1)

相应地其强迫振动方程为

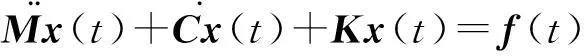
(2)

式中:M∈RN×N----对称系统的质量矩阵;

C∈RN×N----对称系统的阻尼矩阵;

K∈RN×N----对称系统的刚度矩阵。

结构有限元分析时，作拉普拉斯变换x(t)=uewt=uejωt代入式(1)可得

(w2Mu+wCu+Ku)ewt=0

设每个实模态的正则化系数为ai，即

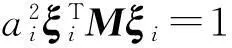
∀i=1,2,…,N

记aiξi=vi，称为无阻尼正则固有振型，简称为振型，则V=[v1,v2，…,vN]为振型矩阵，那么此时模态质量和模态刚度矩阵分别为

(3)

VTKV=diag(k1,k2，…,kn)=

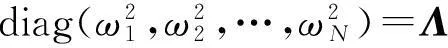
(4)

对经典阻尼系统有

(5)

即模态阻尼矩阵为对角阵，其中阻尼比为

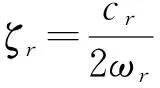
r=1,2,…,N

上面式(3)和式(4)为无阻尼正交条件，应用时有两个问题要注意，一个是要注意标号现象的出现，例如按式(3)所示，应该有

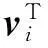
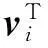
i≠j;i,j=1,2,…,N

但很多应用中，会出现例如下式

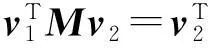
而

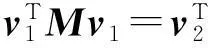
的现象发生，称为标号现象[6]。一旦发现标号现象，要注意调整振型矩阵的标号次序，使式(3)成立。另一个问题是，一般情况下只要是单频结构系统，即系统的固有频率全不相同，那么式(3)就自动满足，但当系统虽为重频系统，也存在式(3)时，那么此重频系统的响应求解也可按文中提及的算法来实现，相当于扩大了文中算法的使用范围。

考虑阻尼时的系统极点及复模态对(λi,ui)(i=1,2,…,2N)满足方程

对于N自由度振动系统，特征方程det[λ2M+λC+K]=0有2N个呈复共轭对出现的特征值λ1,λ2,…,λ2N(其中λi+1为λi的共轭(i=1,3,…,2N-1))，称为系统的极点。这些频率对应着一组呈复共轭对出现特征向量ui∈CN称为系统(1)与λi相对应的第i个模态向量。将u1,u2,…,u2N(其中ui+1为ui的共轭(i=1,3,…,2N-1))称为复模态。它们的正交条件的形式有很多[7]，文中采用如下形式

对于N自由度振动系统，特征方程det[λ2M+λC+K]=0有2N个呈复共轭对出现的特征值λ1,λ2,…,λ2N(其中λi+1为λi的共轭(i=1,3,…,2N-1))，称为系统的极点。这些频率对应着一组呈复共轭对出现特征向量ui∈CN称为系统(1)与λi相对应的第i个模态向量。将u1,u2,…,u2N(其中ui+1为ui的共轭(i=1,3,…,2N-1))称为复模态。它们的正交条件的形式有很多[7]，文中采用如下形式

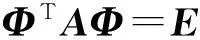
(6)

(7)

其中状态向量矩阵为Φ=[φ1,φ2,…,φ2N]，状态向量为φi=[uiλiui]T(i=1,2,…,2N)，且

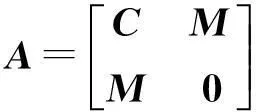
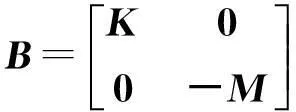
需要说明的是，复模态参数的标号现象可能更为常见，也如前文所述的方法加以处理，即可实现正交式(6)和式(7)，使标号现象并不致妨碍算法的应用。

2非经典阻尼系统动力响应的精确算法比较

当式(5)不能成立，即模态阻尼矩阵VTCV为非对角矩阵，那么系统为非经典阻尼系统。当然，对非经典阻尼系统不能再使用振型迭加法，目前文献[5]中提出了基于频响函数求解非经典阻尼系统的响应的方法。

2.1　基于频响函数法

对振动系统式(2)，取激励为简谐激励，f=[F1,F2,…,FN]Tsinωt，则

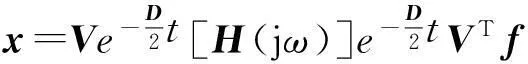
(8)

其中

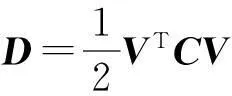
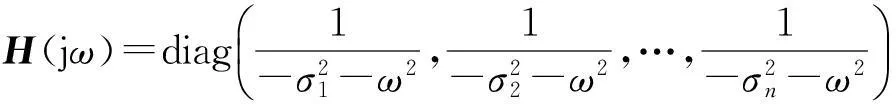
(9)

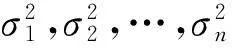
(10)

根据矩阵代数理论，矩阵函数

(11)

2.2　复频率响应

对振动系统式(2)，取激励为f=Fejωt，F=(F1,F2,…,FN)T，其复频率响应为

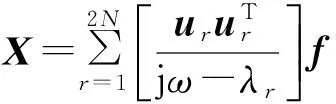
(12)

其复数解Xejωt中取虚部即为对应于简谐激励f=Fsinωt的响应解，这里λi,ui为复模态参数，u1,u2,…,uN为满足正交性条件式(6)的规范化复模态。

3数值算例

文中考虑文献[8]中给出的一个5自由度的质量弹性阻尼系统,此时

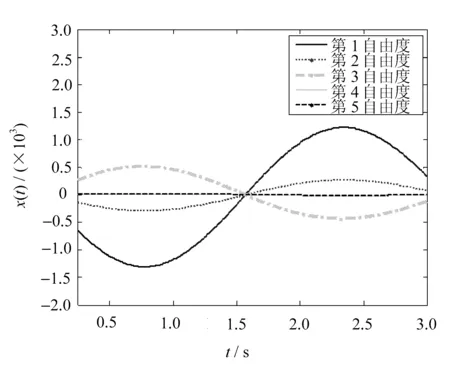
图1　响应的拟合曲线

接下来以第1自由度为例，用复频率响应算法(式(12))来计算响应，并与基于频响函数计算的响应值进行比较，如图2所示。

图2　两种算法计算的第1自由度响应值的对比图

基于频响函数求解非经典阻尼系统的响应方法与N-mark法同时计算系统响应时的比较结果，请参见文献[5]。由文中的数值计算过程及结果可知：

1)复频率响应法与基于频响函数法在理论上都是计算非经典阻尼系统响应的精确算法。

2)但在用复频率响应公式编程计算时，因为使用的是复模态参数，所以出现的标号现象较为严重，且当系统自由度较多时，不仅在调整标号来实现正交条件式(6)时遇到很大困难，而且规范化常数为复数，规范化后ΦTAΦ为近似单位阵，效果并不理想，导致复频率响应计算结果出现较大偏差。而基于频响函数法计算响应的算法在实现过程中，由于使用的是实模态参数，即使出现标号现象，调整标号的工作量也缩小了一倍，而且规范化常数为实数，规范化效果十分精确，体现其良好的工程应用性和计算效率。

4结语

在实际应用中，振型迭加法和相关的里兹向量法，以及直接积分法等各种方法可以组合使用来求解非经典阻尼系统，但多数情况下只能得到数值解。事实上为了更好地理解结构行为，用于谐波分析和响应谱分析，或许无论如何都要计算固有频率和振型，这时由文中的分析可知，基于频响函数的计算响应算法就会体现出良好的操作适应性，尤其可贵的是它得到的是响应的精确解。

参考文献：

[1]Greco A， Santini A. Comparative study on dynamic analysis of non-classically damped linear system[J]. Structural Engineering and Mechanics,2002,14(6):679-698.

[2]张淼，于澜，鞠伟.重频系统的频率灵敏度分析算法研究[J].华南师范大学学报:自然科学版,2014，46(3)：39-43.

[3]郭兴旺，邹家祥.对机械振动系统的六种动态响应分析方法的评述[J].振动与冲击,1996，15(2)：43-46 .

[4]张淼.实模态向量梯度算法[J].长春工业大学学报:自然科学版,2013，34(5)：551-554.

[5]张淼，于澜，鞠伟.基于频响函数矩阵计算阻尼系统动力响应的新方法[J].振动与冲击,2014，33(4)：161-166.

[6]张淼，于澜，鞠伟.复模态正交性理论的异常现象及对策分析[J].应用数学和力学，2014，35(10)：1081-1091.

[7]SondiponA,FriswellMI.Eigenderivativeanalysisofasymmetricnon-conservativesystems[J].InternationalJournalforNumericalMethodsinEngineering,2001,51(6):709-733.

[8]张淼，于澜，鞠伟.重频结构模态灵敏度分析的高精度截模态算法[J].振动工程学报,2014，27(4)：526-532.

Algorithm comparison for the solution of

symmetric non-classical damped system

ZHANG Miao,YU Lan

(School of Science, Changchun Institute of Technology, Changchun 130012， China)

Abstract：Both the frequency response matrix and complex frequency response method are applied to the same problem, for analyzing the transient response, applied condition & range and errors. The features and efficiency of the two algorithms are discussed.

Key words：non-classically damped system; dynamic response; frequency response matrix; label phenomenon.

作者简介：张淼(1972-)，男，汉族，吉林长春人，长春工程学院副教授，博士,主要从事结构优化及振动控制方向研究,E-mail:zm7209@163.com.

基金项目：吉林省教育厅"十二五"科学技术研究项目(2014336)； 2014年国家级大学生创新创业训练项目(201411437028)

收稿日期：2014-06-21

中图分类号：O 321; TB 122

文献标志码：A

文章编号：1674-1374(2015)01-0107-04

DOI:10.15923/j.cnki.cn22-1382/t.2015.1.22