基于扩展Kalman滤波器的永磁同步电机转动惯量辨识研究*

黄苏融，　何栋林，　王　爽，　石　坚

(上海大学 机电工程与自动化学院，上海 200072)



基于扩展Kalman滤波器的永磁同步电机转动惯量辨识研究*

黄苏融，何栋林，王爽，石坚

(上海大学 机电工程与自动化学院，上海 200072)

摘要：为抑制转动惯量变化对高性能伺服系统性能的不良影响，缩短惯量辨识收敛时间和提高辨识精度已成为转动惯量辨识的研究热点。基于扩展Kalman滤波器，开展永磁同步电机转动惯量辨识算法设计、仿真和试验研究。仿真和试验结果表明，扩展Kalman滤波器用于永磁伺服系统的惯量实时辨识是有效的，突变惯量时辨识收敛时间约为4s、辨识误差为6.8%。

关键词：扩展Kalman滤波器； 永磁同步电机； 转动惯量； 参数辨识

0引言

工业机器人、数控机床与新能源汽车等先进制造业的发展，对高性能伺服系统的动态响应、定位准确性提出了更高的要求。但系统的性能受转动惯量的变化影响较大，当转动惯量增大时会使系统响应变慢，容易造成系统不稳定；当转动惯量减小时虽然加快了系统的动态响应速度，但会使速度超调甚至振荡。因此，快速准确地获得转动惯量并应用于永磁同步伺服电机速度控制是提高伺服系统动态性能的有效途径[1-2]。随着交流伺服系统的发展，转动惯量的辨识成为伺服控制技术的重点研究方向之一。

目前，国内外学者提出了多种转动惯量的辨识算法，如最小二乘法、朗道离散时间递推算法、梯度算法、扩展Luenberger观测器(ELO)、扩展卡尔曼(Kalman)滤波器(EKF)等。文献[3]提出在低速时，将加权最小二乘递推法与降维观测器结合起来，把最小二乘辨识出的转动惯量输入到降维观测器中，进一步对转速进行控制，提高了转速控制的精确度。文献[4]采用朗道算法的转动惯量辨识，即在惯量突变时辨识收敛时间最快可控制在5s左右，稳态时辨识误差为0.2%。文献[5]采用扰动转矩观测器方法对永磁同步电机系统的转动惯量进行辨识，试验结果表明该算法的辨识误差近5%，收敛时间约0.6s。文献[6]在分析转动惯量和负载转矩辨识模型的基础上，通过将蚂蚁分布在由不同负载转矩和转动惯量形成的组合区间，提出利用蚁群矢量移动分解算法搜索最优解，同时辨识系统的负载转矩和转动惯量;该算法的惯量辨识具有一定的创新性，但是实现起来比较困难。

扩展Kalman滤波器(Extended Kalman Fileter，EKF)作为一种由最小方差意义上的最优预测估计发展起来的现代滤波方法，因其收敛速度快、估计精度高等优点而受到广泛关注。EKF适用于高性能伺服驱动系统，可以在低速运行下完成转速估计，也可对相关状态和某些参数(转动惯量)进行估计[7-8]。文献[9]提出采用EKF对组合航天器惯量参数进行辨识，该算法克服了由于模型简单导致转动惯量信息辨识不完整的缺点，仿真结果的辨识误差在1%之内。

本文基于EKF，开展了永磁同步伺服电机的转动惯量辨识算法设计、仿真和试验验证，并对该算法的参数选取调整进行分析。仿真和试验结果表明，EKF可以对永磁同步电机控制系统的转动惯量进行准确辨识，突变惯量时辨识收敛时间约为4s、辨识误差为6.8%。

1EKF的惯量辨识

1.1扩展Kalman滤波算法

考虑噪声影响，系统模型离散化的状态方程和输出方程为

(1)

式中： xk——状态变量；

uk——输入量；

yk——输出量；

Ak——系统矩阵；

Bk——输入矩阵；

Ck——测量矩阵；

wk——系统噪声；

vk——测量噪声。

通常情况下，假设wk和vk均为互不相关的零均值高斯白噪声，但实际过程中由于扰动等影响，这个假设并不成立，均为有色噪声信号。它们的协方差矩阵分别为Q和R：

(2)

R=cov(vk)=E(vkvkT)

(3)

EKF状态估计大致分为2个阶段。

(4)

(5)

(6)

式中：P——估计误差协方差矩阵；

G——梯度矩阵。

(2) 校正。利用实际测量值来校正经过上一步预测得到的状态先验估计值：

(7)

(8)

(9)

式中： R——测量噪声的协方差矩阵；

K——Kalman增益矩阵；

H——变换矩阵。

通过上述过程，就可以完成EKF的递推迭代过程估计。在这一过程中，由于状态估计值得到了实际测量值的验证，因而其均方误差变小，可靠性增加。

1.2EKF惯量辨识设计

构建EKF的永磁同步电机转动惯量辨识结构如图1所示。

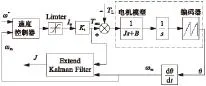
图1　EKF转动惯量辨识结构图

永磁同步电机的机械方程为

(10)

(11)

Tem=KtIq

(12)

式中： ωm——转子机械角速度；

B——摩擦转矩系数；

J——转动惯量；

TL——负载转矩；

θ——转子机械角度；

Kt——转矩常数；

Iq——交轴电流；

Tem——电磁转矩。

在永磁同步伺服电机控制系统中，可以测量得到输出电流和转速，因此选择状态向量为x=[ωmTL1/J]T，输入量uk=Tem，测量得到的输出量yk=ωm，构建永磁同步电机系统的状态方程和输出方程：

(13)

式中： Ts——算法的采样周期。

将式(13)简化成如下形式：

(14)

梯度矩阵：

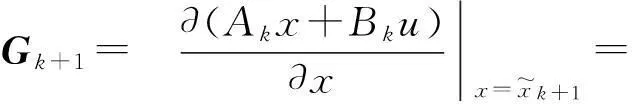
变换矩阵：

1.3参数选取

在EKF转动惯量辨识过程中，参数选取是准确辨识的关键。辨识过程中需要初始条件： 变量初始化状态x(0)，估计误差协方差矩阵P(0)，噪声协方差矩阵Q(0)和测量噪声的协方差矩阵R。常用的方法是试错法调整，通过多次仿真或试验来选择性能最优的初始值。

状态变量初值x(0)与实际初始状态不一致对状态估计的影响不大，随着滤波次数的增加，初值的影响会逐渐减小。系统调试表明，状态变量估计误差协方差矩阵P(0)对系统稳态和动态过程时间影响不大，其数值的改变对转速振幅有一定影响。

为得到较好信噪比的辨识结果，在此将系统噪声协方差矩阵设置为

Q(0)=diag{q11,q22,q33}

参数Q(0)对辨识结果的动态性能和稳定性有很大影响，其中参数变量q11，q22分别对电机转速与负载转矩辨识有影响，q33对转动惯量参数的辨识收敛速度和精度具有直接影响[10]。

编码器的精度决定了测量的电机角度最大误差εM(tk)，电机的角速度可通过式(15)计算：

(15)

式中： T——转过εM(tk)所用的时间。

最大观测误差ΔωM(tk)接近于：

(16)

(17)

本文根据实际情况，反复试凑调整，最终确定EKF参数如下：

x(0)=10-5;

P(0)=diag{1，1，10};

Q(0)=diag{10-5，10-5，0.1};

R=0.05。

2仿真与试验

在MATLAB/Simulink仿真环境中构建了基于EKF的永磁同步电机转动惯量辨识的模型。

整个控制系统采用Id=0的矢量控制策略，其中EKF辨识算法使用S函数实现，S函数的输入为电机机械角速度和电磁转矩，开关控制频率10kHz。电机参数如表1所示。

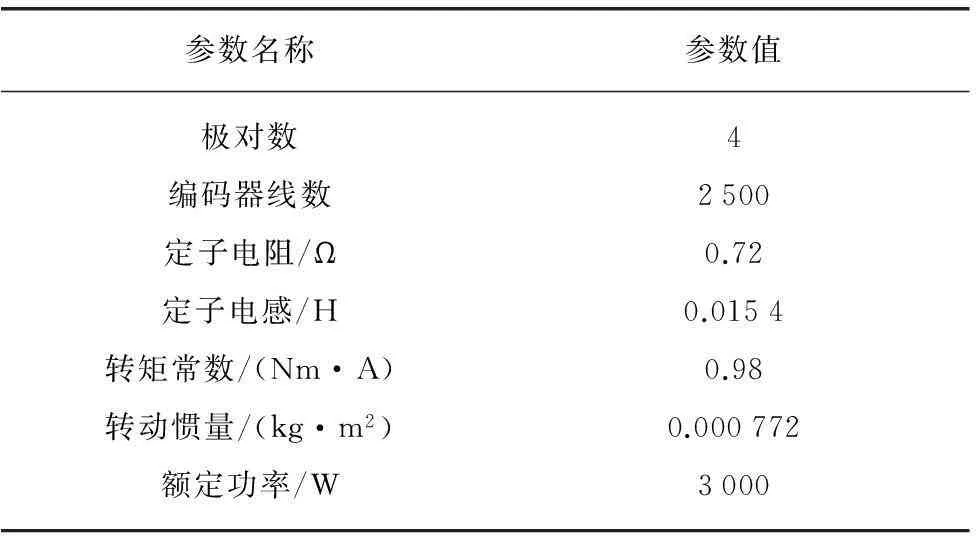
表1　电机参数表

由电机机械方程可知，转动惯量J与角速度变化率dωm/dt以乘积的形式出现。当角速度稳定不变时，EKF无法辨识转动惯量，所以只有电机角速度发生一定变化时才能辨识出转动惯量J。为模仿电机转速振荡信号，仿真中给定方波转速信号作为理想测试信号，转速的幅值在 200r/min 和300r/mim之间交替变化，变化的频率为25Hz[11]，取惯量辨识周期Ts=125μs。

空载运行时，系统的转动惯量即为电机转子的转动惯量，J=0.000772(kg·m2)，采用EKF算法转动惯量辨识结果如图2所示，收敛时间近0.16s，辨识误差约0.5%。

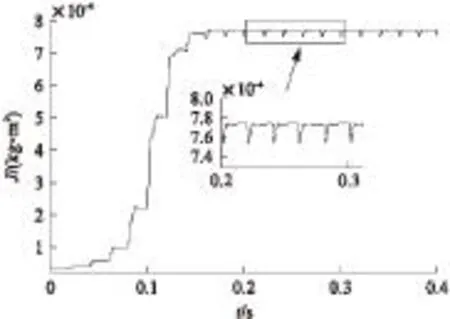
图2　空载转动惯量辨识

为了测试EKF在突变惯量下的辨识效果，在t=0.3s时突加4J大小的负载惯量JL，整个系统的总惯量值为ΣJ=5J=0.00386(kg·m2)。仿真结果如图3所示，图3(a)为突变惯量的EKF的辨识结果，图3(b)中n为电机转速，Iq为交轴电流。

从图3所示的仿真结果中看出，EKF能快速辨识转动惯量，当突加负载惯量时，电机转速和Iq电流波形相应变差，EKF辨识收敛速度约0.12s、辨识误差约为3.2%。

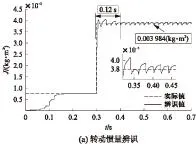
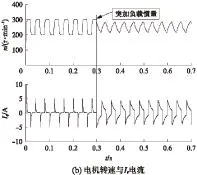
图3　突变转动惯量(ΣJ=5J)

在永磁同步伺服电机控制实时仿真测试平台上搭建基于EKF的永磁同步电机惯量辨识试验，参数与表1相同，试验平台如图4所示。

图4　试验平台

由于EKF矩阵运算的计算量较大，同时受所采用dSPACE硬件本身运算速度的限制，试验中给定方波速度振荡周期为2s，转速的幅值在200r/min 和300r/min之间交替变化。试验辨识结果如图5所示，时刻①开始空载转动惯量辨识，时刻②转动惯量由J变化到2J。

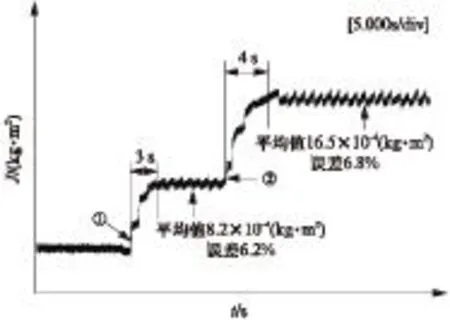
图5　EKF转动惯量试验结果

从图5的试验结果发现，采用EKF对永磁同步电机的转动惯量进行辨识，收敛时间约为3s、空载时辨识误差近6.2%；当系统的转动惯量从J突变为2J时，收敛时间约为4s、辨识误差近6.8%。无论是空载转动惯量还是变转动惯量的情况，EKF算法均能比较准确的实现辨识。

由于EKF的运算量大，本文所采用的硬件目前仅以2s周期的方波转速振荡信号进行试验，造成算法收敛的绝对时间较长。但是随着以后采用更高速度的控制芯片，惯量辨识收敛速度也将随着转速振荡周期的减小而成比例提高。

在高性能伺服系统中，转动惯量辨识至关重要。本文基于EKF，开展永磁同步电机伺服系统转动惯量辨识研究，仿真和试验结果表明EKF转动惯量辨识算法可以对转动惯量进行有效地辨识，突变惯量时，辨识收敛时间约为4s、辨识误差为6.8%。

【参 考 文 献】

[1]徐东，王田苗，魏洪兴. 一种基于简化模型的永磁同步电机转动惯量辨识和误差补偿[J]. 电工技术学报，2013，28(2)： 126-131.

[2]JIN J, WANG S, HUANG S. Adaptive disturbance observer design for servo drive system with time-varying load inertia[C]∥2014 IEEE International Conference on Mechatronics and Automation (ICMA), 2014： 1504-1508.

[3]YAN S, XU D, WANG G, et al. Low speed control of PMAC servo system based on reduced-order observer[C] ∥Intelligent Robots and Systems, 2006 IEEE/RSJ International Conference on. IEEE, 2006： 4886-4889.

[4]鲁文其，胡育文，梁骄雁，等. 永磁同步电机伺服系统抗扰动自适应控制[J]. 中国电机工程学报，2011，31(3)： 75-81.

[5]LI S, LIU Z. Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia[J]. IEEE Transactions on Industrial Electronics, 2009, 56(8)： 3050-3059.

[6]王少威，万山明，周理兵，等. 利用蚁群算法辨识PMSM伺服系统负载转矩和转动惯量[J]. 电工技术学报，2011，26(6)： 18-25.

[7]NGUYEN K Q, NGUYEN T H, HA Q P. FPGA-based sensorless PMSM speed control using reduced-order extended kalman filters[J]. IEEE Transactions on Industrial Electronics, 2014,61(12)： 6574-6582.

[8]张猛，肖曦，李永东，等.基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J]. 中国电机工程学报，2007，27(36)： 36-40.

[9]杨雅君，廖瑛，刘翔春. 航天器转动惯量参数在轨辨识的最优激励[J]. 国防科技大学学报，2014，36(5)： 29-43.

[10]SCHUTTE F, BEINEKE S, ROLFSMEIER A, et al. Online identification of mechanical parameters using extended Kalman filters[C] ∥Industry Applications Conference, 1997, Thirty-Second IAS Annual Meeting, IAS’97, Conference Record of the 1997 IEEE, 1997(1)： 501-508.

[11]梁骄雁，胡育文，鲁文其. 永磁交流伺服系统的抗扰动自适应控制[J]. 电工技术学报，2011，26(10)： 174-180.

欢迎投稿欢迎订阅欢迎刊登广告

*基金项目： 教育部博士点基金(20113108110008)；上海经息委产学研合作项目(沪CXY-2013-20)

Research on Inertia Identification of Permanent Magnet Synchronous

Motor Based on Extend Kalman Filter

HUANGSurong，HEDonglin，WANGShuang，SHIjian

(School of Mechatronic Engineering and Automation, Shanghai University, Shanghai200072, China)

Abstract：To suppress the bad effect of inertia change on high performance servo system, shorten the inertia identification convergence time and improve the accuracy become a hot research topic. Based on extend Kalman filter, design, simulation and experiment were researched. The simulation and experiment results showed that the extend Kalman filter algorithm was effective, when the inertia was changed, the convergence time of identification was about 4s and the identification error was 6.8%.

Key words：extend Kalman filter; permanent magnet synchronous motor (PMSM); inertia; parameter identification

收稿日期：2015-01-30

中图分类号：TM 351

文献标志码：A

文章编号：1673-6540(2015)12- 0007- 05

通讯作者：黄苏融