单折太阳翼支承点分布优化分析

李郑发， 曹登庆， 张迎春

(1.深圳航天科技创新技术研究院，广东 深圳　518057；2.哈尔滨工业大学 航天学院，哈尔滨　150001； 3. 深圳航天东方红海特卫星有限公司，广东 深圳　518054)



单折太阳翼支承点分布优化分析

李郑发1,2,3， 曹登庆2， 张迎春1,3

(1.深圳航天科技创新技术研究院，广东 深圳518057；2.哈尔滨工业大学 航天学院，哈尔滨150001； 3. 深圳航天东方红海特卫星有限公司，广东 深圳518054)

折叠式太阳翼结构成为现代航天器设计中最为常见的一种形式。它即能满足航天器能源的需求又能适应搭载空间的约束。在发射阶段，太阳翼通过压紧机构折叠于航天器本体侧壁上，当航天器入轨后，压紧机构释放后太阳翼展到预定平面内。单折太阳翼相比多折叠太阳翼具有高可靠性的优点，随着航天技术的发展，航天器的小型化和能源利用效率的提高，单折太阳翼结构形式在微小卫星构型设计中将得到广泛应用。太阳翼结构是航天器上最为关键的结构之一，在发射阶段其力学环境十分恶劣，使得人们对太阳翼结构的动力学特性尤为关注[1-2]，而太阳翼支承点的位置对其固有特性的影响十分敏感。

典型的小卫星单折太阳翼通常由两个铰链和两个压紧点与卫星本体连接，其两个铰链位于太阳翼基板一边，而压紧点通常位于基板内，是典型的四点弹性支承约束下的矩形板结构形式。多年来，国内外学者对点支承板结构系统的自由振动问题开展了相关研究：Gorman[3]基于薄板振动问题的经典解析解，采用叠加方法求解四点对称支承矩形板的振动问题。Narita等[4]利用双幂级数试函数，并根据Ritz法分析了对称四点支承正交异性矩形板、带内部点支承正交异性悬臂板和任意多点支承正交异性椭圆板的自由振动问题。许琪楼[5]将四角点支承四边自由矩形板振形函数表达式由四边自由板所固有的基本振形和角点力所激发的附加振型组成,对四角点支承四边自由矩形板自振进行了分析。Lopatin等[6]由哈密尔顿原理推导了四边自由中心单点支承矩形板的振动方程，并基于广义Galerkin法获得较为精确的系统固有频率。Saadatpour等[7]也基于Galerkin法研究了一般形状的矩形板含有内部点支承或线支承的振动特性。Bapat等[8]采用柔度函数法分析了位于板自由边界和内部多点支承的矩形板的振动。该方法是在自由边界或内部支点处添加一个虚拟的弹性约束条件，并构造一个柔度函数满足其在约束条件处位移边界条件。王砚等[9]采用无网格Galerkin法分析了四边简支板的固有频率与点弹性支承的刚性系数和支承位置之间关系,并分析了点弹性支承的刚性系数和支承位置对矩形薄板横向振动特性的影响。Wang等[10]利用Rayleigh-Ritz法研究了一条边和单点约束下矩形板的固有频率，并对支承点位置对固有频率的影响开展讨论。Huang等[11]利用有限层法对内部含弹性点支承矩形薄板横向振动问题开展了相关研究。此外，对点支承矩形薄板振动特性的其它相关研究,可参阅相关文献[12-18]。

从上述研究工作中可以看出没有针对典型的单折四点支承太阳翼结构振动特性的研究报道。本文主要针对典型小卫星单折太阳翼结构的振动特性及支承点的分布对固有特性的影响进行深入分析。主要根据能量守恒原理和Rayleigh-Ritz理论推导出单折太阳翼的横向振动方程和频率方程。通过数值分析详细地研究了压紧点在不同位置对其基频影响的变化规律，以基频最大化为优化目标对其支承点的分布进行优化分析，并将理论分析结果与有限元分析结果进行比较和验证。

1折叠翼振动方程的建立

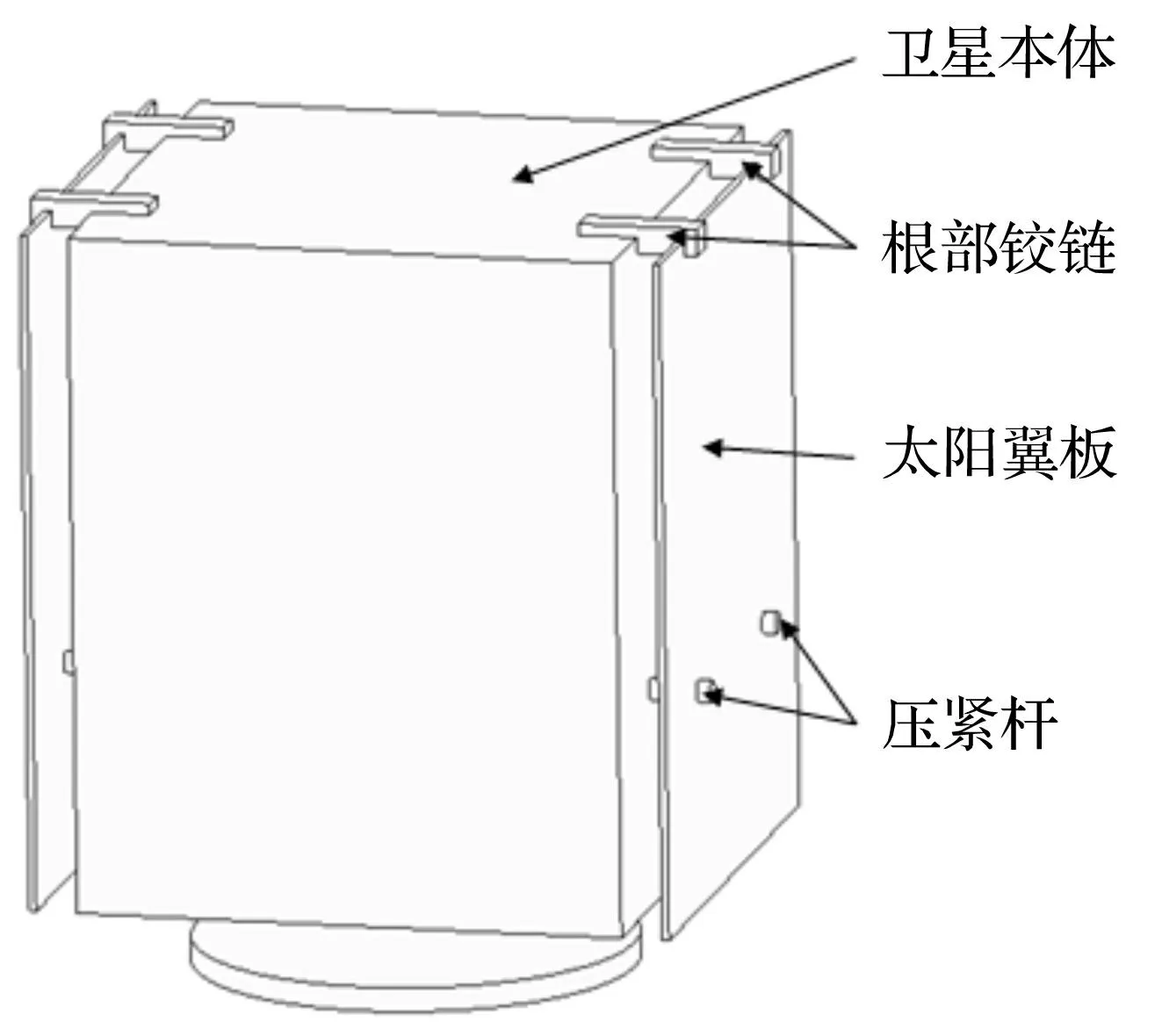
图1　点支承太阳翼结构示意图Fig.1 Thesolar panel supported with distributed point supports

多数情况下，航天器在构型布局时优优先考虑太阳翼压紧点和铰链安装位置的设计，其原因在于太阳翼面积相对较大，且支承点数量要尽量少，而支承点位置对太阳翼固有特性的影响十分敏感。图1给出的是典型四点支承单折矩形太阳翼折叠状态示意图，太阳翼通过两个根部铰链和两个压紧杆与卫星本体连接。

不同航天器其根部铰链和压紧杆以及与航天器结构连接处对太阳翼的弹性约束都完全不同。航天器初步设计时在对如图1所示的四点支承太阳翼固有特性分析时可以不考虑压紧杆和铰链对翼板的弹性约束，将其简化如图2所示的力学分析模型。假设矩形太阳翼板的边长分别为a,b，厚度为h，其两边分别位于坐标轴上ξ,ζ,支承点分别位于A、B、D和C处,四边处于自由状态。其中A、B处为太阳翼铰链的安装位置，D和C为太阳翼压紧点的位置。假设铰链处的等效刚度为k1，压紧点出的等效刚度为k2。

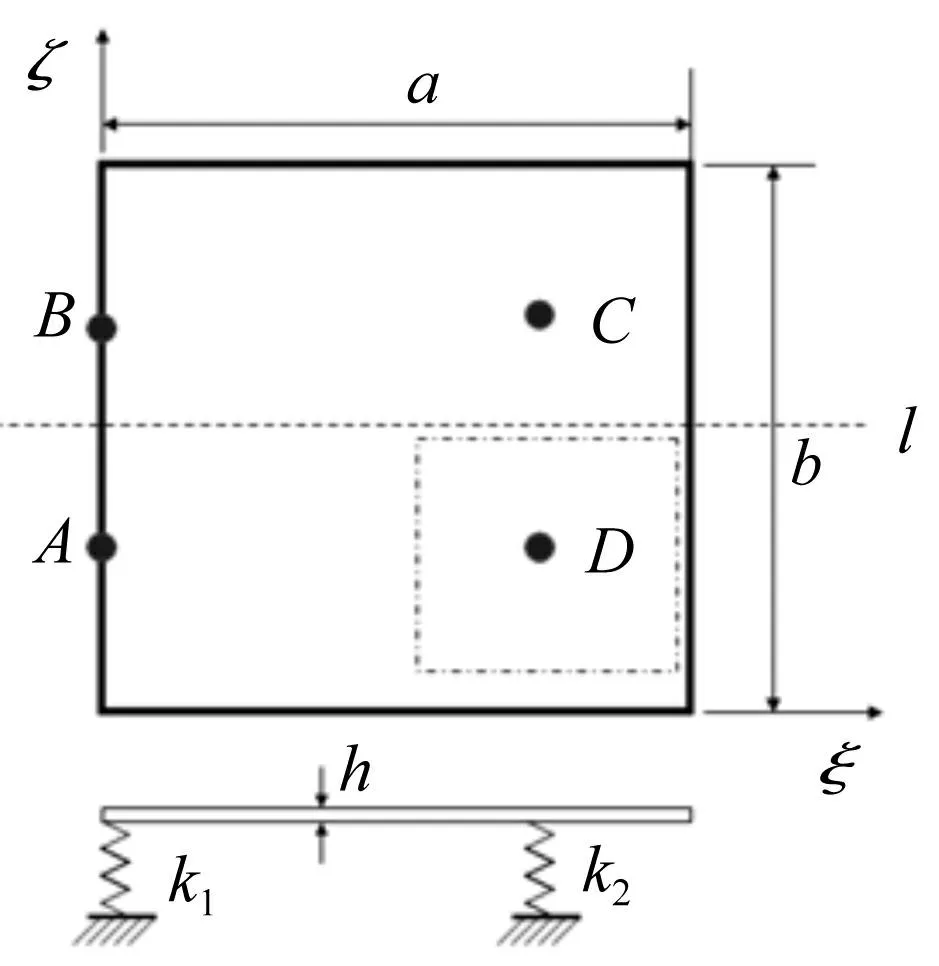
图2　折叠太阳翼力学分析模型Fig.2 The analytical model of folding solar panels

当翼板横向自由振动时，假设其挠度函数可以表示：

w(ξ,ζ,t)=W(ξ,ζ)sin(ωt)

(1)

式中：ω为振动角频率，W(ξ,ζ)为板横向振动形函数。

不考虑实际太阳翼结构上的太阳电池片和太阳翼基板复合材料的非均匀性等因素，将太阳翼简化为均质各向同性材料的板结构。那么，翼板在横向振动过程中的动能T和势能U分别表示为：

(2)

(3)

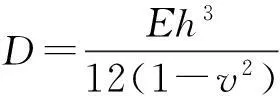
(4)

为了便于分析,引入无量纲参数x=ξ/a、y=ζ/b。将式(1)代入(2)-(4)式整理得到太阳翼板振动的最大动能Tp-max和最大变形势能Up-max，以及压紧杆和铰链等效弹簧的最大势能Us-max为分别为：

(5)

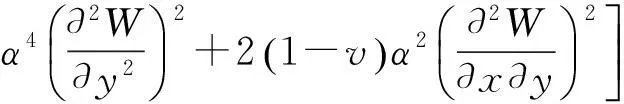
(6)

(7)

式中：长宽比α=a/b，无量纲挠度函数为W(x,y)。

由能量守恒原理得到折叠太阳翼的振动方程为：

Us-max+Up-max-Tp-max=0

(8)

为了便于叙述令：

Π=Us-max+Up-max-Tp-max

(9)

2固有频率方程的建立

当找到合适的挠度函数为W(x,y)(能够满足其位移边界条件)，则由方程(8)就可以获得系统的固有频率。假设其挠度函数为如下形式：

(10)

式中,Amn为待定参数；Xm(x)和Yn(y)分别采用自由梁的振动本征函数[13]表示：

Xr=cosh(λrx)+cos(λrx)-

γrsinh(λrx)-γrsin(λrx)

(11)

Yr=cosh(λry)+cos(λry)-

γrsinh(λry)-γrsin(λry)

(12)

其中:r>2，式中参数λr、γr满足如下关系式：

cosh(λrx)cos(λrx)=1

(13)

(14)

将振型函数(10)代入到方程(8)，由Rayleigh-Ritz法对待定系数Amn进行一阶偏导得到如下方程：

(15)

把式(11)~式(14)代入到方程式(15)，并利用本征函数的正交性得到系统的频率方程为：

(16)

式中：I为单位矩阵，Kmnij、Ks-mnij和η分别表示为：

(17)

(18)

η=ρhω2a4/D

(19)

(20)

(21)

式中：m,i=1,2,3,…,M；n,j=1,2,3,…N;r,t=0,1,2。

确定方程(10)振型函数W(x,y)中项数M、N后，通过方程(16)可以求得参数η，从而由式子(19)得到系统的固有频率f：

(22)

3支承点分布优化分析

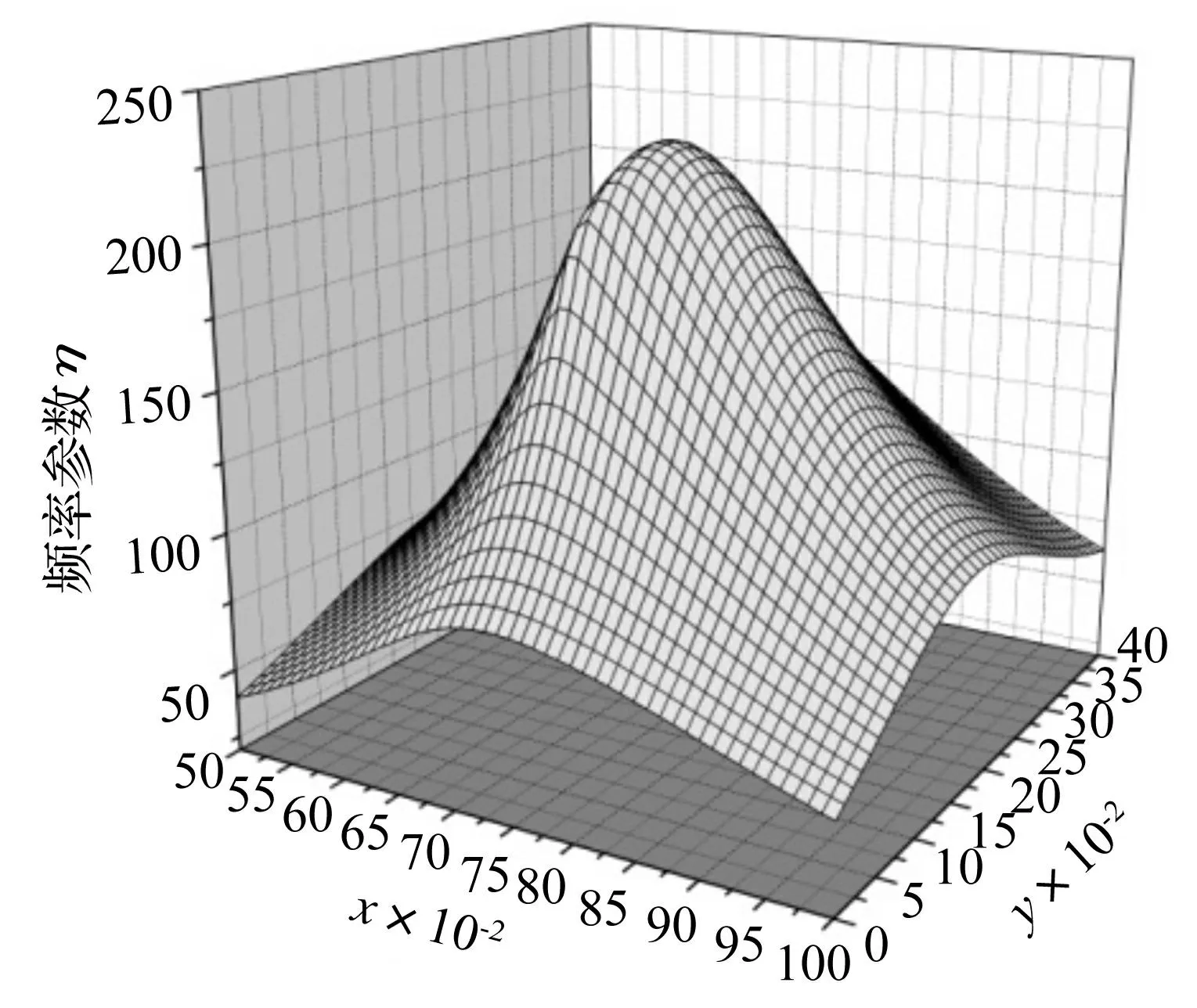
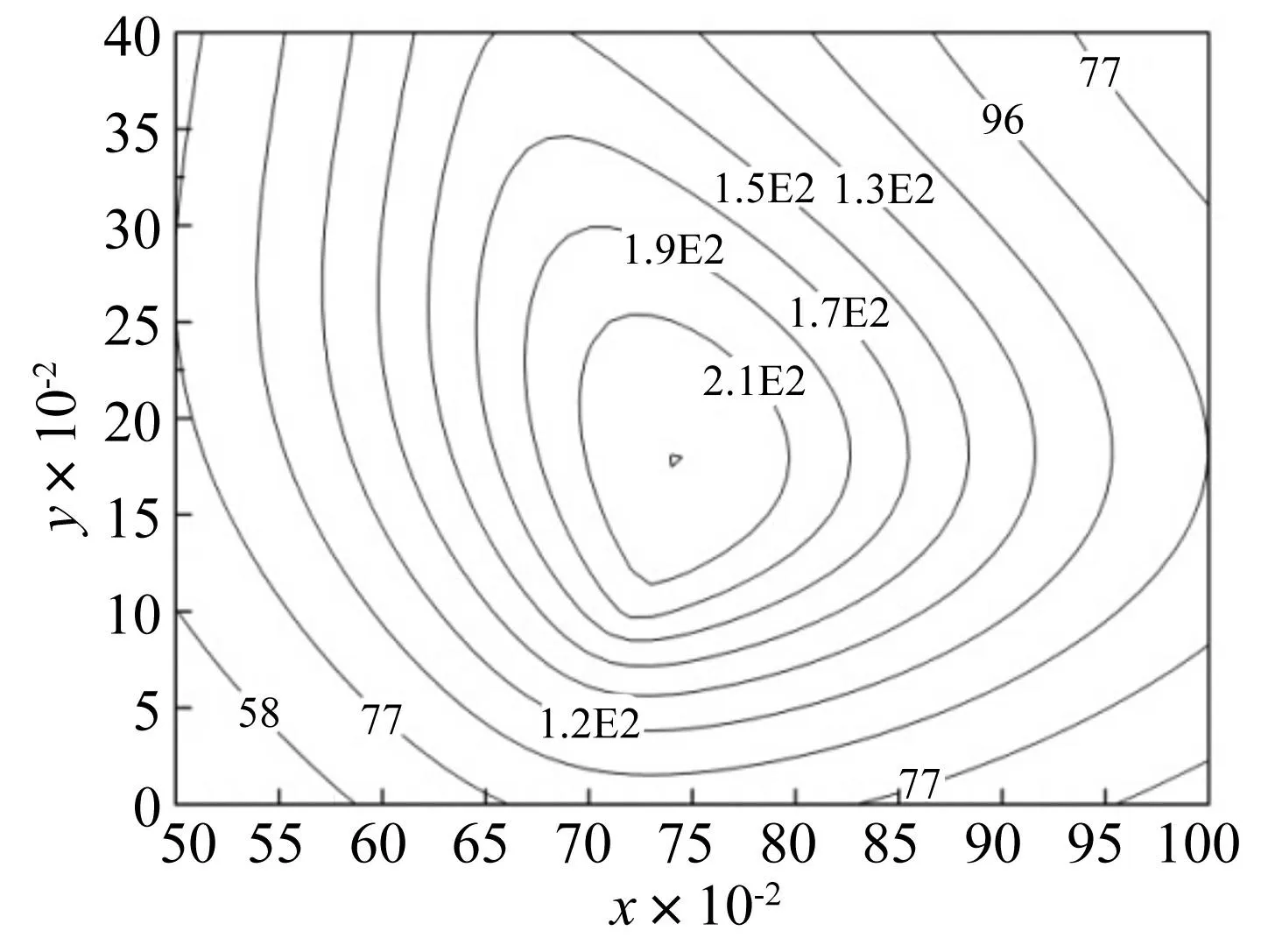
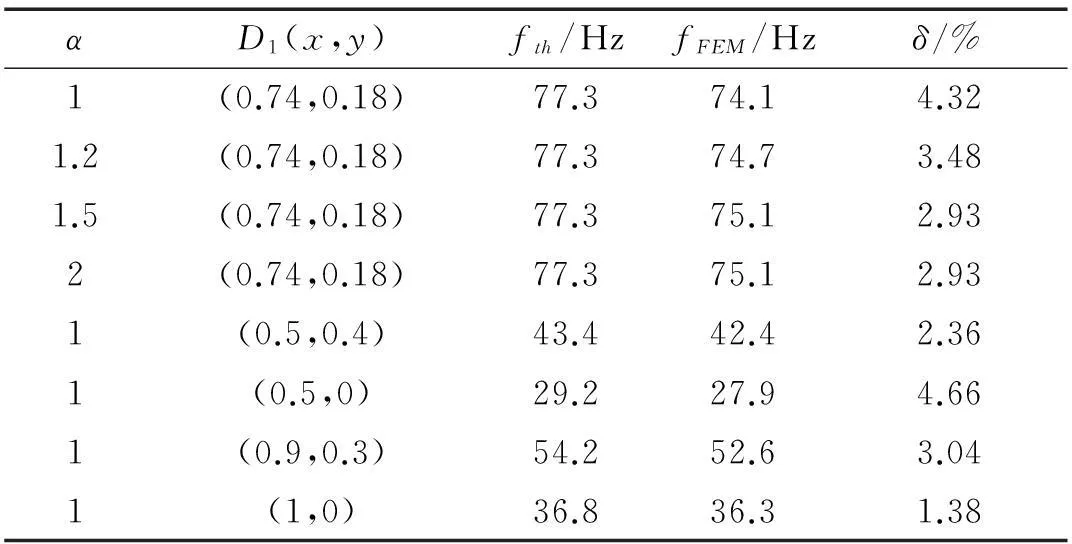
如图1所示的典型四点支承单折矩形太阳翼，其四个支承点关于太阳翼板中心线l对称，且A、B之间距离与C、D之间的距离相等。因此，当D点的位置确定后其余三点位置都已明确。为了快速获得支承点D的最佳位置(即结构基频最大支承点位置)，初步判断最优支承点位置位于区域:0.5

图3　参数η与支承点D位置关系Fig.3 The relationship of parameter(η)versus the support location(D)

图4　参数η等值线分布图Fig.4 The isoclines distribution of parameter η

从图4可以看出，D点位于：{x=0.74,y=0.18}处(假定为O点)系统基频频率参数η取得最大值。其等值曲线图表明，远离O点的支承位置系统基频逐渐减小，支承点处同一等值线上的系统基频是相等，即除O点外系统处于相同频率的支承点位置有无穷多个，其分布特点与等值线分布相同。

对该系统在不同长宽比条件下进行数值分析，但其支承点D均位于{x=0.74,y=0.18}处，其分析结果如图5。从图5可以看出长宽比α在1≤α≤2范围内取值对系统参数η的影响很小，仅在227.5<η<229.5范围内变化，如果取其中间值228.5来计算其频率，引起的误差仅在-0.21%~0.218%之间。因此，长宽比α的变化对系统的频率影响很小，可以近似取值为228.5得到系统的最大基频的近似计算公式为：

(23)

图5　参数η与长宽比α关系Fig.5 Curves of parameter η versus side ratio α

为了验证上述理论公式的有效性,选取4种不同长宽比的太阳翼结构将其理论计算结果fth(采用式(23)计算)和有限元分析结果fFEM进行比较，结果见表2所示。其相关参数见表1所示。其中有限元分析采用通用Patran&Nastran前后处理和求解软件。采用4节点四边形Bending Panel单元对整板进行网划分，单元长度为0.03 m；采用表1中材料参数对单元属性进行赋值；通过约束4个支承点处节点3个平动来模拟边界条件。

从表2中可以看出其理论计算结果与有限分析结果相比较都偏大，但是其偏差仅在5%以内,能够满足绝大部分工程应用要求。其存在误差的主要原因在于振型函数W(x,y)中项数取得较少，实际工程中，可以根据要求来适当选取振型函数中项数，从而达到需要的精度要求，此外该方法求解折叠太阳翼结构的一阶固有频率是一种近似求解方法而非精确解。

表1　矩形板参数

表2　基频分析结果

4结论

对典型小卫星单折太阳翼结构的振动特性及支承点的分布位置对固有特性的影响进行了深入研究,获得了单折太阳翼的频率方程。当支承点D位置位于{x=0.74,y=0.18}处时系统的基频最大,且矩形太阳翼的长宽比对系统最大基频影响很小，仅在±0.22%以内。给出了便于近似求解系统最大基频的式(23)，并通过算例分析表明该公式具有较好的工程应用精度。本文分析结果对太阳翼支承点位置的初步设计以及相关结构的初步设计具有十分重要应用价值。

参 考 文 献

[1] 王巍, 于登云, 马兴瑞. 航天器铰接结构非线性动力学特性研究进展 [J]. 力学进展, 2006, 36(2): 233-238.

WANG Wei, YU Deng-yun, MA Xing-rui. Advances and trends of non-linear dynamics of space joint dominated structure [J]. Advances in Mechanic, 2006, 36(2): 233-238.

[2] 方宝东. 卫星收拢太阳翼频率响应分析 [J]. .机械设计与研究, 2005, 21(3):95-97.

FANG Bao-dong. Analysis of the frequency response characters of satellite solar cell array [J]. .Machine Design and Research, 2005, 21(3):95-97.

[3] Gorman D J. An analytical solution for the free vibration analysis of rectangular plates resting on symmetrically distributed point supports [J]. Journal of Sound and Vibration, 1981, 79:561-74.

[4] Narita Y, Hodgkinson J M. Layerwise optimisation for maximising the fundamental frequencies of point-supported rectangular laminated composite plates [J]. Composite Structures, 2005, 69:127-35.

[5] 许琪楼.四角点支承四边自由矩形板自振分析新方法[J]. 振动与冲击,2013, 32(3):83-86.

XU Qi-lou. A new analysis method of free vibration of rectangular plate with 4-free-sides and 4-corner point supports [J]. Journal of Vibration and Shock, 2013, 32(3):83-86.

[6] Lopatin A V, Morozov E V. Fundamental frequency of an orthotropic rectangular plate with an internal centre point support [J]. Composite Structures, 2011, 93:2487-2495.

[7] Saadatpour M M, Azhari M, Bradford M A. Vibration analysis of simply supported plates of general shape with internal point and line supports using the Galerkin method [J]. .Engineering Structures. 2000, 22:1180-1188.

[8] Bapat A V, Suryanarayan S. Free vibrations of rectangular plates with interior point supports [J]. Journal of Sound and Vibration, 1989, 134:291-313

[9] 王砚,王忠民,阮苗. 无网格法在点弹性支承矩形薄板横向振动中的应用[J]. 计算力学学报.2010, 27(2):238-243.

WANG Yan, WANG Zhong-min, Ruan Miao. Application of meshless method in the transverse vibration of rectangular thin plate with elastic point supports [J]. Chinese Journal of Computational Mechanics, 2010, 27(2):238-243.

[10] Wang D, Yang Z C, Yu Z G. Minimum stiffness location of point support for control of fundamental natural frequency of rectangular plate by Rayleigh-Ritz method [J]. Journal of Sound and Vibration, 2010, 329:2792-2808.

[11] Huang M H, Thambiratnam D P, Free vibration analysis of rectangular plates on elastic intermediate supports [J]. Journal of Sound and Vibration, 2001, 240:567-580.

[12] Zhao Y B, Wei G W，Xiang Y. Plate vibration under irregular internal supports[J].International Journal of Solids and Structures 2002, 39:1361-1383.

[13] Kerstens J G M. Vibration of a rectangular plate supported at an arbitrary number of points [J]. Journal of Sound and Vibration, 1979, 65(4):493-504.

[14] Zhou D, Cheung Y K, Kong J. Free vibration of thick, layered rectangular plates with point supports by finite layer method[J]. International Journal of Solids and Structures 2000, 37:1483-1499.

[15] Wang C M, Wang Y C, Reddy J N. Problems and remedy for the Ritz method in determining stress resultants of corner supported rectangular plates [J]. Computers and Structures，2002，80:145-154.

[16] Katsikadelis J T, Sapountzakis E J, Zorba E G. A BEM approach to static and dynamic analysis of plates with internal supports [J]. Computational Mechanics, 1990，7:31-40.

[17] Zhou D, Cheung Y, Kong J. Free vibration of thick, layered rectangular plates with point supports by finite layer method [J]. International Journal of Solids and Structures 2000, 37:1483-99.

[18] Zhou D, Ji T. Free vibration of rectangular plates with internal column supports[J]. Journal of Sound and Vibration, 2006, 297:146-66.

第一作者 李郑发 男，博士，高工，1983年8月生

摘要：支承点的分布对折叠太阳翼动力学特性有显著影响。为了研究压紧点分布对折叠太阳翼固有频率的影响，以典型的单折点支承太阳翼为研究对象，根据能量守恒原理和Rayleigh-Ritz理论推导出点支承单折太阳翼的振动方程和频率方程。研究了四点对称支承太阳翼结构系统的固有动力学特性，并以基频最大为优化目标对其支承点的分布进行优化分析。通过算例分析表明其理论计算结果与有限元分析结果具有较好的一致性。研究结果对太阳翼支承点分布的初步设计提供了理论分析依据。

关键词：太阳翼；优化分析；Rayleigh-Ritz法；基频；点支承

Optimization of supporting points distribution for single folding solar panels

LIZheng-fa1,2,3,CAODeng-qing2,ZHANGYing-chun1,3(1. Shenzhen Academy of Aerospace Technology, Shenzhen 518057, China;2. The School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;3. Shenzhen Aerospace Dongfanghong HT Satellite Ltd. CAST, Shenzhen 518054, China)

Abstract:The distribution of supporting points has a significant impact on dynamic characteristics of a folding solar panel. In order to study the effect of supporting points distribution on the fundamental frequency of folding solar panel, a typical single folding solar panel supported at four points was taken as the investigation object. Based on the energy conservation principle and Rayleigh-Ritz theory, a vibration equation and a frequency equation were established for analyzing the free vibration of folding solar panel with points support. The vibration characteristics of the folding solar panel symmetrically supported at four points were solved, and aiming at achieving the maximum fundamental frequency, the optimization of support points distribution was also discussed. The examples show the theoretical calculation results have good consistency with the results of the finite element analysis. The research results could provide a theoretical basis for the preliminary design of supporting points distribution for single folding solar panels.

Key words:solar panel; optimization analysis; Rayleigh-Ritz method; fundamental frequency; points support

中图分类号:O326

文献标志码：A DOI:10.13465/j.cnki.jvs.2015.24.029

收稿日期：2014-10-16修改稿收到日期：2014-12-18

基金项目：国家自然科学基金项目(91216106);国家重大基础研究项目资助