基于绝对节点坐标法的柔性多体系统灵敏度分析

王铁成， 陈国平， 孙东阳

(1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京　210016; 2.重庆大学 航空航天学院 ，重庆　400044)



基于绝对节点坐标法的柔性多体系统灵敏度分析

王铁成1， 陈国平1， 孙东阳2

(1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京210016; 2.重庆大学 航空航天学院 ，重庆400044)

机械系统优化设计可以提高机械系统的精度和稳定性。为了避免优化参数选择的盲目性，提高设计效率，进行近似分析和预测设计趋势，首先就需要对系统参数进行灵敏度分析。因此，灵敏度分析已经成为机械系统动力学分析与优化设计的桥梁，并成为机械系统优化设计的核心问题。

灵敏度计算方法主要有直接微分法和伴随变量法。直接微分法是通过计算系统的运动学或动力学方程对设计变量的偏导数，得到目标函数对设计变量的灵敏度。潘振宽等[1]采用直接微分法对多刚体系统进行了灵敏度分析。针对递推形式建立的链状多体系统，Haug等[2]采用直接微分法对其进行了灵敏度分析。直接微分法的优点是直观，易于理解，但随着系统设计变量的增多，求解规模成倍增长，导致灵敏度求解的效率降低。伴随变量法是通过引入伴随变量，使多设计变量系统灵敏度分析计算效率得到提高，该方法已经在多体系统的灵敏度分析中得到了重视和应用[3]。Etman等[4]采用伴随变量法对多体系统动态特性进行了灵敏度分析。Li等[5]和Maly等[6]基于隐式微分代数方程，推导了多体系统灵敏度分析的伴随变量法。目前，多体系统灵敏度分析大多是针对刚体系统，柔性多体系统灵敏度分析的研究还比较少。主要原因是柔性多体系统具有高维数和强非线性特性，导致分析相对困难。虽然浮动坐标法是最常用的一种柔性多体系统建模方法，但是该方法基于小变形假设，用于分析存在大变形的柔性多体系统会带来较大误差。Shabana等[7]提出了多柔性体绝对节点坐标建模方法，该方法的理论基础是有限元和连续介质力学[8-9]，由该方法推导的多体系统方程的质量阵为常数矩阵，且不存在科氏力和离心力项。为了对存在大变形的柔性多体系统进行灵敏度分析，同时考虑到多变量情况下伴随变量法有更高的计算效率，本文采用伴随变量法对基于绝对节点坐标法建立的柔性多体系统进行了灵敏度分析，并将其计算结果与直接法的计算结果进行了比较。

1绝对节点坐标建模的动力学方程

基于绝对节点坐标法的一维两节点梁单元如图1所示，单元上任意点的位置矢量可表示为：

(1)

式中：e为单元节点坐标，S是定义在总体坐标系上的形函数，分别表示如下[7]

(2)

图1　平面梁单元Fig.1Plane beam element

(3)

式中:s1=1-3ξ2+2ξ3，s2=ξ-3ξ2+2ξ3，s3=3ξ2-2ξ3，s4=l(ξ3-ξ2)，这里ξ=x/l。

根据式(1)，单元的动能可表示为

(4)

式中:Me=∫ρSTSdV，为单元的常数质量阵，ρ和V分别是材料的密度和单元的体积。

根据连续介质力学理论，单元的总应变能包含弯曲应变能Uel和轴向拉伸应变能Uet，表示为

(5)

式中：εi和κ分别为单元应变和曲率。

基于虚功原理建立单元的动力学方程表示为

(6)

其中:Qe为单元受到的广义外力，Qk为单元广义弹性力。

单元广义弹性力由单元应变能对单元坐标求偏导获得，即

(7)

式中：Kl和Kt分别表示单元的轴向拉伸非线性刚度阵和弯曲线性刚度阵。

则含约束的柔性体k的动力学方程为

(8)

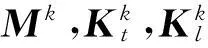
其中:Be为布尔矩阵。

2灵敏度分析

伴随变量法计算灵敏度，需要先求解动力学方程，然后根据动力学计算结果，逆向求解伴随变量为未知量的微分方程组，其中，动力学计算结果需要拟合函数，可使在伴随变量微分方程的数值计算时，能取得在所计算时间内的任意时刻的函数值。

本文选用积分型目标函数对绝对节点坐标法建模的柔性多体系统进行灵敏度分析。目标函数设为

(9)

状态变量和设计变量分别为

q=[q1q2…qn]T

(10)

b=[b1b2…bl]T

(11)

多体系统动力学方程和约束方程分别为

(12)

Φ(q,b,t)=0

(13)

为了计算灵敏度，先用莱布尼兹法对目标函数求导，得到

(14)

(15)

(16)

引入伴随变量μ和ν，分别乘以式(12)和式(13)并积分得

(17)

(18)

式(17)和式(18)对设计变量求导得

ΦTqbλ+ΦTqqλqb-Qb-Qqqb)dt=0

(19)

(20)

(21)

其中

将式(15)，式(20)和式(21)相加得

(22)

选取伴随变量使得积分式中qb和λb前的系数分别等于零，得如下关于伴随变量的微分代数方程

(23)

Φqμ-Fλ=0

(24)

(25)

再由式(25)推出下面两式

(26)

(27)

采用绝对节点坐标法建立的柔性多体系统动力学方程，质量矩阵M为满秩常数阵，进一步可得到

(28)

(29)

根据初始条件式(28)、(29)，逆向求解关于伴随变量的微分代数方程组(23)、(24)，将计算结果代入式(16)，得目标函数灵敏度

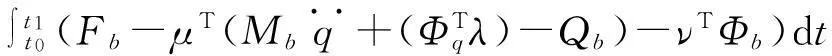
(30)

3算例分析

本文以受重力作用的矩形截面柔性单摆系统为研究对象，如图2所示。

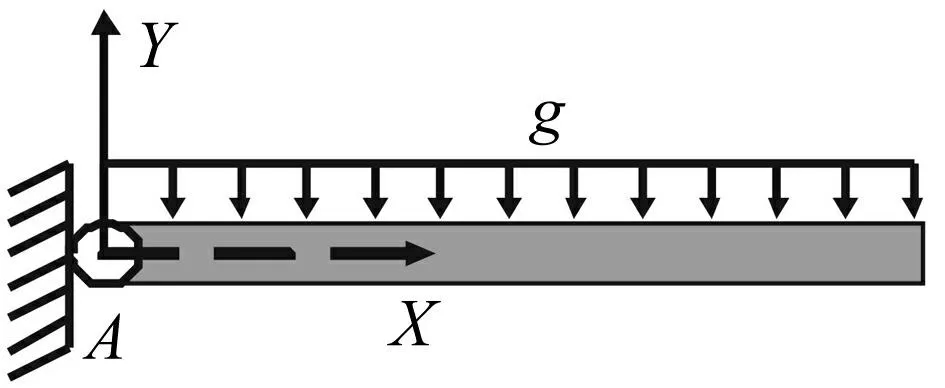
图2　柔性单摆Fig.2 Flexible simple pendulum

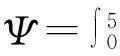
表1　两种方法的灵敏度计算结果

表1给出了分别采用伴随变量法和直接微分法得到的目标函数对单摆的密度、弹性模量、长度、截面长度和宽度的灵敏度。同时对比了两种方法计算结果的相对误差，可以发现，其相对误差都在4%以内。而且可以发现，目标函数对单摆长度、截面长度和宽度的变化比较敏感，而密度和弹性模量对目标函数的影响很小。采用直接微分法计算的单摆末端横向位移对五个设计变量的灵敏度如图3~图7所示，由图可知五个设计变量中长度的变化对末端横向位移的影响最明显，这与基于目标函数的灵敏度分析结论一致。

图3 x对ρ的灵敏度Fig.3Thesensitivityofxwithrespecttoρ图4 x对E的灵敏度Fig.4ThesensitivityofxwithrespecttoE图5 x对l的灵敏度Fig.5Thesensitivityofxwithrespecttol

图6　x对a的灵敏度Fig.6 The sensitivity of x with respect to a

图7　x对b的灵敏度Fig.7 The sensitivity of x with respect to b

为了分析伴随变量法和直接微分法的计算效率，对比了五个设计变量情况下两种方法的计算时间，如表2所示。 可以看出，考虑一个设计变量时，伴随变量法所用计算时间多于直接微分法，约为直接微分法计算时间的2倍；考虑两个设计变量时，两种方法的计算时间基本相当；三个设计变量时，伴随变量法所用时间约为直接微分法的75%，当五个设计变量的情况时，伴随变量法的计算时间约为直接法计算时间一半。由此可见，随着设计变量的增加，伴随法的计算效率将高于直接微分法。这主要是因为随着设计变量的增多，伴随变量法随之增加的计算时间主要就在灵敏度积分函数上，在此算例中大概耗时25 s左右，而直接微分法随着设计变量增加，需要再计算一组微分方程，势必增加求解时间。

表2　两种方法的计算时间

4结论

本文对基于绝对节点坐标法建立的柔性多体系统进行了灵敏度分析。以矩形截面的柔性单摆系统为例，以工程上常用的积分型函数为目标函数，使用伴随变量法和直接微分法分别计算了目标函数对柔性体长度、弹性模量、密度、截面的长度和宽度的灵敏度。通过分析发现，两种方法计算结果的相对误差均在4%以内，因此，计算结果是可靠的。同时可以发现随着设计变量的增加，伴随变量法比直接法有更高的计算效率。为工程上，采用伴随变量法对存在大变形的柔性多体系统的进行灵敏度分析提供了理论依据。

参 考 文 献

[1] 潘振宽，丁洁玉，王钰. 基于隐式微分/代数方程的多体系统动力学设计灵敏度分析方法[J]. 动力学与控制,2004, 2(2): 66-69.

PAN Zhen-kuan, DING Jie-yu, WANG Yu. Design sensitivity analysis of multibody system dynamics descrided by implicit differential/algebraic[J]. Journal of Dynamics and Control,2004, 2(2): 66-69.

[2] Haug E J,Neel K M, Krishnasawami P. Design sensitivity analysis and optimization of dynamically driven systems[M]. Computer Aided Analysis and Optim-ization of Mechanical System Dynamics.Springer Berlin Heidelberg,1983:555-636.

[3] 康新忠, 王宝元. 机械系统动态优化设计的灵敏度方法[J]. 机械工程学报, 1990, 13(1): 18-23.

KANG Xin-zhong, WANG Bao-yuan. Sensitivity analysis method of the dynamic optimal design for mechanical systems[J]. Journal of Vibration Engineering,1990, 13(1): 18-23.

[4] Etman L F P, Van Campen D H, Schoofs A J G. Optimization of multibody systems using approximation concepts[C]//IUTAM.Symposium on Optimization of Mechanical Systems. Netherlands：Springer，1996：81-88.

[5] Li S, Petzold L. Software and algorithms for sensitivity analysis of large-scale differential-algebraic systems[J]. Journal of Computational and Applied Mathematics, 2000, 125:131-145.

[6] Maly T, Pctzold L R. Numerical methods and software for sensitivity analysis of differential-algebraic systems[J]. Applied Numerical Mathematics, 1996, 20: 57-59.

[7] Shabana A. An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies[R]. University of Illionis at Chicago, 1996.

[8] Shabana A. Computational continuum mechanics[M]. New York: Cambridge University Press, 2011.

[9] Bonet J, Wood R. Nonlinear continuum mechanics for finite element analysis[M]. Cambridge: Cambridge University Press, 1997.

第一作者 王铁成 男，博士生，1979年生

摘要：针对多个设计变量情况下的柔性多体系统灵敏度分析，采用伴随变量法对基于绝对节点坐标法建立的柔性多体系统进行了研究。为了验证的该方法的计算效率，分别采用直接微分法和伴随变量法对受重力作用的柔性单摆进行了研究, 结果表明：这两种方法计算结果的误差很小，随着设计变量数量的增加，伴随变量法有更高的计算效率。

关键词：多体系统;绝对节点坐标法;灵敏度;伴随变量法

Sensitivity analysis of flexible multibody systems based on absolute nodal coordinate formulation

WANGTie-cheng1,CHENGuo-ping1,SUNDong-yang2(1. The State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;2. College of Aerospace Engineering, Chongqing University, Chongqing 400044, China)

Abstract:For multiple design variables, an adjoint variable method was applied in sensitivity analysis of flexible multibody systems based on the absolute node coordinate formulation. In order to verify the computational efficiency of the method, a flexible pendulum under gravity was analysed by using the direct differentiation method and the adjoint variable method respectively. The results show that the errors of the two methods are both small, and the adjoint variable method has higher computational efficiency with the increase of design variables.

Key words:multibody system; sensitivity; absolute node coordinates formulation; adjoint variable method

中图分类号:O313.7

文献标志码：A DOI:10.13465/j.cnki.jvs.2015.24.015

通信作者陈国平 男，教授，博士生导师，1956年生

收稿日期：2014-09-04修改稿收到日期：2014-11-26

基金项目：江苏高校优势学科建设工程资助项目