RBF网络在无刷直流电机控制系统的应用*

李书舟，邓小龙

(1湖南电气职业技术学院汽车工程系，湖南湘潭 411000；

2中国电器科学研究院，广东广州510300)



RBF网络在无刷直流电机控制系统的应用*

李书舟1，邓小龙2

(1湖南电气职业技术学院汽车工程系，湖南湘潭 411000；

2中国电器科学研究院，广东广州510300)

摘要研究了无刷电机的控制问题，针对常规PID控制的无刷直流电机系统存在参数难以整定、超调量大、调节时间长、抗干扰能力差等问题，建立了无刷直流电机的数学模型，提出了RBF神经网络控制在系统中的总体设计方法，并在常规PID控制器的基础上建立了RBF网络控制器；利用Matlab软件对常规PID控制和RBF网络控制进行仿真比较，结果表明基于RBF网络控制器能动态调整控制器参数，有效的提高了系统的性能以及控制效果，系统对参数扰动具有较强的鲁棒性。

关键词无刷直流电机；RBF神经网络；Matlab；PID控制器

0引言

二十世纪八十年代，鲍威尔首次提出了基于多变量函数插值的径向基函数(Radical Basis Function RBF)方法，此后RBF神经网络的研究得到了中外学者的广泛关注[1]。RBF神经网络和其他前向神经网络一样，有相似的三层前馈神经网络结构，模拟人脑中局部调整、相互覆盖和接收的神经网络结构，具有运算能力强、速度快以及局部函数逼近的特点，所以它在智能控制、信息处理等领域的应用有着广阔的前景[2]。

传统控制理论在无刷直流电机系统的控制中，主要以状态方程、微分方程及各种变换的方法进行研究，计算本质上仍是数值方法。譬如经典PID控制方法在高频扰动时，电机速度抖动频繁，缺乏对干扰变化的应变能力，而常规自适应方法参数调整难，实现成本高，难以确保有好的控制效果[3]。文献[4]针对横向永磁电机的调速特点提出了一种RBF神经网络整定PID参数的控制方法，实时整定修正PID系统控制参数，但对系统抗干扰性能未做分析；文献[5]提出了一种RBF神经网络的无刷直流电机调速控制新策略，具有较好的速度响应与超调性，但未给出参数自适应整定曲线。

本文将研究RBF神经网络整定PID控制无刷直流电机系统上的应用。在此基础上，研究了其在无刷直流电机系统中的控制效果。建立了无刷直流电机的数学模型，利用神经网络的非线性适应能力来优化无刷直流电机的PID控制参数，实现对无刷直流电机的有效控制。最后，在控制系统中广泛存在的阶跃响应进行了仿真实验，得出了系统阶跃曲线。结果表明，利用RBF神经网络控制，系统具有更好的鲁棒性[6]。

1无刷直流电机数学模型

无刷直流电机由电机本体、转子位置传感器和电子换相线路三大部分组成。定子上导磁的定子铁心及导电的电枢绕组设计时要求结构简单，运行可靠，并能产生足够的磁动势以得到足够的转矩，转子采用瓦形磁钢，进行特殊的磁路设计，可获得梯形波的气隙磁场，电子换相电路同时能按照位置传感器的信号进行正确换向和控制，能够实现电机的正反转，并且能满足不同环境条件和长期运行的要求。

以两相导通星形三相六状态为例，分析BLDC的数学模型及电磁转矩等特性。为了便于分析，假定电机定子三相完全对称，空间上互差120°；三相绕组电阻、电感参数完全相同；转子永磁体产生的气隙磁场为方波，三相绕组反电动势为梯形波；忽略定子绕组电枢反应的影响；电机气隙磁导均匀，磁路不饱和，不计涡流损耗；电枢绕组间互感忽略。可得到无刷直流电机的数学模型如式(1)所示[7]。

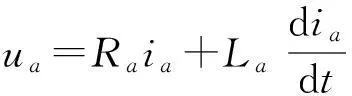
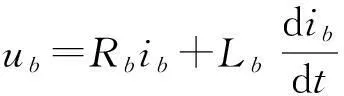
(1)

式中，ua,ub,uc,un—三相端电压和中点电压(V);ea,eb,ec—三相电子反电动势(V)；ia,ib,ic—三相电子相电流(A)；La,Lb,Lc—三相电子自感(H)；Ra,Rb,Rc—三相电子绕组的相电阻(Ω)。

由电机的结构决定，在360°电角度内，转子的磁阻不随转子位置的变化而变化，并假定三相绕组对称，则有La,Lb,Lc相等，Ra,Rb,Rc相等。

由于三相对称的电机中，ia+ib+ic=0，以及Mib+Mic=-Mia,un=0，则式(1)可改写为状态方程

(2)

式中，P—微分算子。

在电机运行过程中，电磁转矩的表达式为

Te=(eaia+ebib+ecic)/ω

(3)

式中，ω—转子角速度(rad/s)。

电机的机械运动方程为

(4)

式中，f—阻尼系数( N·m·s/rad)；J—电机转动惯量(k g·m2)；TL—负载转矩( N·m)。

反电动势系数ke由以下公式计算

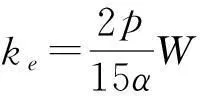
(5)

式中，W—电枢绕组每相串联的匝数；φ—每极磁通(Wb)。

电机运行过程中瞬态功耗的公式为

(6)

式中，Ω—电机角速度；P—功耗。

2RBF神经网络控制算法

2.1　常规PID控制算法

PID控制器是由三种运算集合而成，它包括比例调节(P)、积分调节(I)、微分(D)调节。系统误差经过三种运算调节后，将得到的计算结果作为控制量，反馈回系统形成闭环控制。其形式见式(7)。

(7)

式中，e(t)—采样输出与基准信号相减后的偏差信号；kp、ki、kd—比例系数、积分系数和微分系数。运算得到的u(t)作为系统输入，反馈回系统中。

同样，在数字控制系统中，使用比较普遍的也是PID控制规律。在传统的PID控制中，存在比例、积分、微分这三种控制作用。比例控制的优点是:误差一旦产生，控制器立即就有控制作用，使被控制量朝着误差减小的方向变化，其控制作用的强弱取决于比例系数kp。比例控制的缺点是对于系统阶跃响应值为一有限值的被控对象存在静差。加大其值可以减小静差，但kp过大时，会破坏系统的动态性能，甚至使闭环系统不稳定。

积分控制的优点是：它能对误差进行记忆并积分，有利于消除静差。积分控制的缺点在于积分作用具有滞后特性。如果积分控制作用太强就会使系统的动态性能变差，甚至使系统变得不稳定。

微分控制的优点是：它能对误差进行微分，敏感于误差的变化趋势，增大微分控制可以加快系统响应，使超调量减小，增加系统稳定性。它的缺点是对于干扰同样敏感，使系统抑制干扰能力降低。

2.2　RBF神经网络模型

RBF神经网络模型由鲍威尔于1985年提出，它是神经网络中最典型的模型。具有结构简单、全局最优、训练速度快等优点，很适合解决分类问题。与多层网络结构类似，它是由三层网络结构组成的前向神经网络模型，如图1所示。它包括输入层，隐含层和输出层。输入层用来将输入变量xn传输到隐含层。隐含层调整神经元的变换函数一径向基函数R的参数，对输入做出响应，输入层与隐含层之间权值为1。而输出层通过对响应进行加权whn来得到相应的输出。其中，径向基函数是非负的非线性函数并且关于中心点对称。

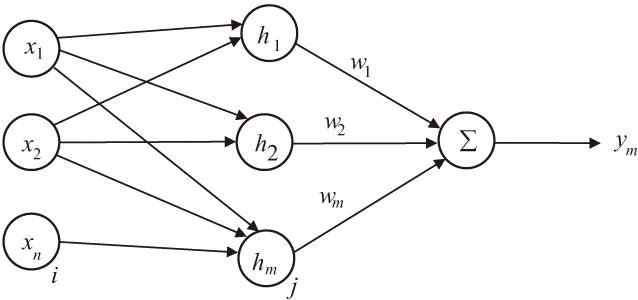
图1　RBF神经网络结构

RBF网络分两部分：第一部分是输入层与隐层的连接，对输入向量进行一次变换，将n维空间的输入数据变换到m维空间内，即实现X→hj的非线性映射，其表达式为

hj=fj(x1,x2,…,xn)

(8)

式中，j=1，2，…，m,f(x)—RBF神经网络的径向基函数。

第二部分是隐层与输出层的连接，对隐层神经元的输出线性加权求和得到网络输出，即实现hj→ym的线性映射，其表达式为

(9)

式中，ωj—中间层神经元和输出层神经元的权值；hj—径向基函数。

2.3　RBF神经网络控制算法

RBF神经网络中的径向基函数有几种常用的函数形式[6]，选取高斯函数为RBF神经网络的径向基函数，其表达式为

(10)

式中，Cj—第j个RBF节点的中心向量；bj—第j节点RBF幅宽参数，且大于零。

当RBF神经网络的结构确定以后，网络中需要学习调整的参数包括隐层神经元中心、基宽参数和隐层至输出层的连接权值。

设k时刻对象的实际输出为yk，RBF神经网络的输出为ym,k，则取网络的性能指标函数为

(11)

根据梯度下降法，输出权、中心节点及节点宽度参数的迭代算法为

ωj=ωj,k-1+η(y0,k-ym,k)hj+

α(ωi,k-1-ωi,k-2)

(12)

(13)

bj,k=bj,k-1+Δbj+α(bj,k-1-bj,k-2)

(14)

(15)

cji,k=cjk,k-1+Δcji,k+α(cji,k-1-cji,k-2)

(16)

式中，η—学习速率；α—动量因子。

通过RBF神经网络辨识，可以得到对象输出对输入的敏感度为

(17)

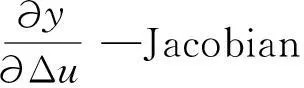
采用增量式PID控制器，误差为

ek=ydk-yk

(18)

PID三相输入为

(19)

控制算法为

Δuk=kpek-ek-1+kiek+kdek-2ek-1+ek-2

(20)

3仿真

通过以上分析，在Matlab7.0中编写仿真程序，考虑到模型的复杂性，直接建立Simulink模型不易，将S函数与Simulink框图相结合，建立仿真模型，同时单神经元控制与传统PID算法进行对比，用以验证单神经元控制的鲁棒性[8]。

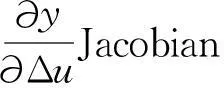
图2　Jacobian信息变化

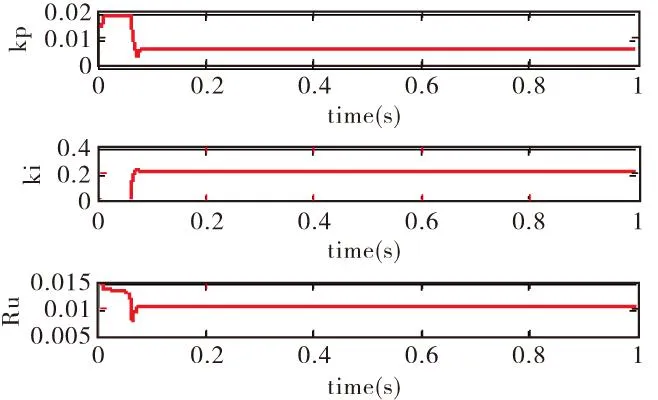
图3　PID参数变化

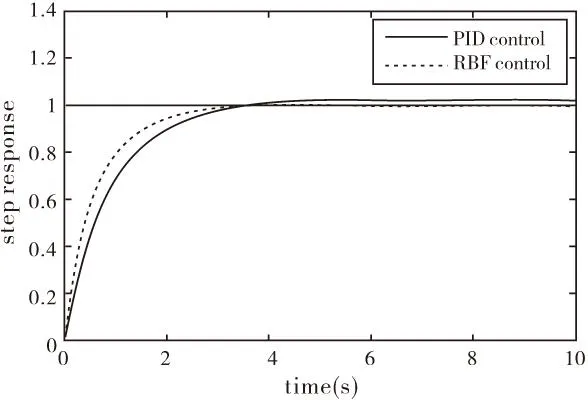
图4　两种控制模式下的阶跃响应

由图2、图3、图4可以看出，引入RBF神经网络控制系统的Jacobian信息以及PID参数都进行动态调整，RBF网络控制与传统PID控制相比在系统的快速性及准确性上都得到了提高。

4结语

本文针对无刷直流电机控制模式进行了研究。结合无刷直流电机的特性，建立了系统的数学模型，采用了RBF神经网络控制器，确定了RBF神经网络的控制模式及控制算法。采用Matlab/Simulink进行仿真。结果表明，与传统的PID控制相比，基于RBF网络控制的无刷直流电机系统有更优越的动态性能和稳态性能，系统具有较好的鲁棒性。

参考文献

[1]何玉彬，李新忠.神经网络控制技术及其应用[M].北京:科学出版社，2000.

[2]杨旭华.神经网络及其在控制中的应用研究.浙江大学博士学位论文，[D].2004:2-3.

[3]Naira Hovakimyan, Flavio Nardi, Anthony Calise and Nakwan Kim. Adaptive Output Feedback Control of Uncertain Nonlinear Systems Using Single-Hidden-Layer Neural Networks. Neural Networks, 2002, 13(6):1420-1431.

[4]庞明,史仪凯,杨宁.RBF网络在横向磁场永磁电机调速系统中的应用[J].计算机测量与控制,2012,20(8):2236-2239.

[5]胡云宝,王加祥,曹闹昌.基于RBF神经网络无刷直流电机调速系统[J].微电机,2013,46(1):63-66.

[6]甘敏，彭辉.不同基函数对RBF-ARX模型的影响[J].中南大学学报(自然科学版)，2010，41(6)：2230-2235.

[7]纪志成,沈艳霞,姜建国.基于Matlab无刷直流电机系统仿真建模的新方法[J].系统仿真学报,2003,15(12):1745-1749.

[8]刘金琨.先进PID控制Matlab仿真[M].北京:电子工业出版社,2011.

Application Research of RBF Network to Control System

of Brushless DC Motor

LiShuzhouandDengXiaolong

(1.Department of Automotive Engineering, Hunan Electrical College of Technology, Xiangtan 411000, China；2.China Electric Appliance Science Research Institute, Guangzhou 510300, China)

AbstractThis paper researches control problem of brushless motor. For difficult parameter tuning, large overshoot, long regulation time and poor anti-interference ability of brushless DC motor with conventional PID control system, a mathematical model of brushless DC motor is established, overall design method of RBF neural network control is presented, and RBF network controller based on conventional PID controller is established. The simulative comparison between conventional PID control and RBF network control is carried out by Matlab software, the results show that RBF network controller can dynamically adjust parameters of controller and effectively improve system performance and control effect. The system has strong robustness to parameter perturbation.

Key wordsBrushless DC motor；RBF neural network；Matlab；PID controller

收稿日期：2015-07-28

作者简介：李书舟男1979年生；硕士研究生，现从事自动控制方面的研究工作.

基金项目：2012年湖南省教育厅高等学校科学研究项目(12c1005)

中图分类号：TM301.2;TM33

文献标识码：A

文章编号：1008-7281(2015)06-0010-004

DOI:10.3969/J.ISSN.1008-7281.2015.06.04