基于开放线圈系统金属探测仪传感器的特性分析

王茹茹,　宋开宏,　明　军,　潘煜天,　吴振飞

(安徽大学 电子信息工程学院,安徽 合肥　230601)



基于开放线圈系统金属探测仪传感器的特性分析

王茹茹,宋开宏,明军,潘煜天,吴振飞

(安徽大学 电子信息工程学院,安徽 合肥230601)

摘要:针对金属探测仪传感器设计时缺少理论分析的现状,文章基于开放式矩形平衡线圈模型,推导了金属杂质通过平衡线圈时产生的附加感应电动势,并进行仿真,得到了金属探测仪传感器平衡线圈的最佳尺寸比例以及金属杂质通过平衡线圈的最佳空间探测位置。通过实验验证了该计算方法的正确性,为进一步提高金属探测仪的检测灵敏度和稳定性提供了理论依据。

关键词:金属探测仪;传感器;矩形平衡线圈;感应电动势;空间位置

金属探测装置在日常生活和工业生产中有着广泛的应用,因此研究金属探测技术有着重要意义。金属探测的方法主要有基于单线圈的频率检测法、阻抗检测法和基于平衡线圈的差分电压检测法[1]。其中,平衡线圈技术在国外许多高精度金属探测仪产品中已经得到应用[2]。平衡线圈模型具有2种结构,即开放式和闭合式[3]。开放式线圈结构具有抗干扰能力强、灵敏度高等优点,因此得到了广泛的应用。目前,金属探测仪传感器制作主要依靠经验,对线圈尺寸比例以及金属最佳探测位置缺少严格的理论分析[4]。

本文基于金属探测仪传感器的矩形平衡线圈物理模型,根据电磁感应原理[5]、涡流效应以及平衡线圈的差动接收理论[6]进行理论分析,得出探测金属信号与线圈尺寸以及位置相关的解析表达式,并对此进行仿真分析,确定探测金属的最佳位置,为选择传感器线圈尺寸比例以及金属最佳探测位置提供理论依据。

1物理模型

金属探测仪传感器的物理模型如图1所示,发射线圈1与接收线圈2、线圈3上下平行排列,发射线圈尺寸为2x0×2y0,接收线圈尺寸2a1×(b1-b0),发射线圈位于xoy平面,接收线圈与发射线圈之间的距离为z0,W为金属异物,金属看成圆薄片,半径为r0。发射线圈中通有角频率为ω的交变电流i1=I1msinωt。2个接收线圈采用平衡差动的连接方式送入差分放大电路,当没有金属时,由于对称性,发射线圈的磁场使2个接收线圈中产生的感应电动势大小相同,方向相反,从而使得2个线圈中的感应电动势相互抵消,接收线圈的磁场处于平衡态。

图1　传感器的物理模型

当有金属目标进入磁场范围,由于电磁感应会在金属内部产生感应电动势,金属中会产生涡流,涡流将会激发磁场,其与发射线圈产生的磁场相互叠加,增强或者减弱原来的激励磁场。由于金属目标离2个接收线圈的位置不同,2个接收线圈接收到的信号也不同,差分电路会输出一个反映金属大小和属性的电平信号。当金属目标的位置、大小、电导率以及磁导率不同时,2个接收线圈接收到的信号的幅度和相位也不同,通过对获得电平信号的幅度和相位信息来探测和区分金属异物。

2理论分析

根据毕奥-萨伐尔定律[7]可以推导出发射线圈1在空间任一点产生的磁感应强度B1的z轴分量B1z,即为四条边的叠加:

(1)

其中，B1zm为磁感应强度B1的z轴分量B1z的幅值[8]；B11z、B12z、B13z、B14z分别为发射线圈的4条边产生的磁感应强度的z轴分量,其值如下:

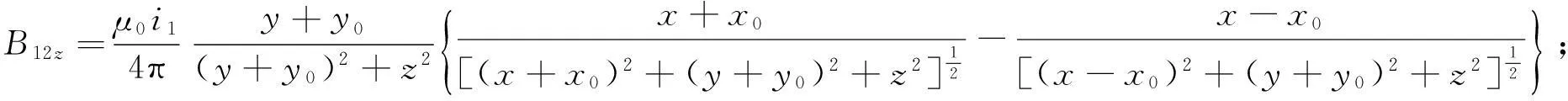
由法拉第电磁感应定律可知发射线圈1的磁场[9]对接收线圈2产生的感应电动势e12为:

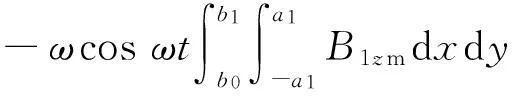
(2)

其中，S2、Φ12分别为接收线圈2的面积和其磁通量。

由于对称性,同理可推导出发射线圈1的磁场使接收线圈3产生的感应电动势e13:

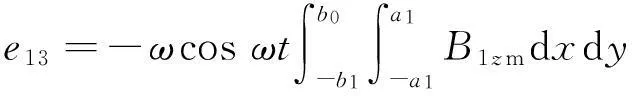
(3)

由Mathematics 4.0验证可知:

(4)

这说明在没有金属异物的情况下,接收线圈2、3的感应电动势大小相等,方向相反,差分输出为0。

设金属异物为半径为r0的圆薄片,μr、ρ、h分别为金属异物的相对磁导率、电阻率和趋肤深度，其轴线与z轴平行,将金属片上的磁场看成是相等的,可计算出发射线圈1在金属片上产生的涡流[10]iw为:

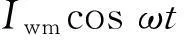
(5)

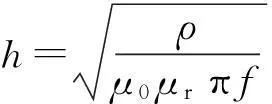
由(1)式可推导出通有电流i2的接收线圈2在空间任一点产生的磁感应强度B2的z轴分量B2z以及接收线圈3在空间任一点产生的磁感应强度B3的z轴分量B3z。

(6)

同理,接收线圈3与金属片之间的互感M3W为:

(7)

通有电流iw的线圈W在接收线圈2和3中产生的附加感生电势eW2和eW3分别为:

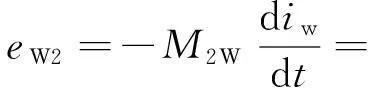
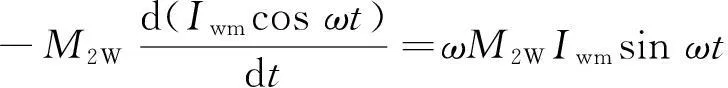
(8)

(9)

接收线圈1、线圈2上产生的差分感应电动势之差为:

(10)

当有金属通过时,e的幅值随金属的位置不同而变化,据此可以检测出是否有金属通过。

3仿真结果

线圈尺寸为:y0=10 cm,x0=40 cm,z0=40 cm,b0=0 cm,b1=10 cm,a1=40 cm,r0=0.3 cm,f=8.0×104Hz,金属目标为铜且沿着y轴方向水平通过。

3.1　感应电动势随水平位置的变化

取z=39 cm、x分别为0、30、40 cm时,在y方向上接收线圈2、线圈3的差分感应电动势随着金属的移动的变化如图2所示。

由图2可知:

(1) 在y方向上接收线圈的差分感应电动势在靠近接收线圈外边界时幅值较小,在接近线圈内边界时幅值较大。

(2) 在x位置上,金属沿着线圈中心即x为0 cm时感应电动势的幅值最大,灵敏度较高,越靠近边缘灵敏度越小。

图2　差分感应电动势随y位置的变化

3.2　感应电动势随垂直位置的变化

当金属处于不同垂直位置时,电动势随着y的变化也会产生很大变化,如图3所示。

由图3可以看出:随着z的增加差分感应电动势的最大值的绝对值eM多次出现极值,任一个确定的z值对应存在一个最大的绝对值eM。eM先减小后增大,z趋于z0=40 cm或0时,eM的值都比较大,z等于20 cm时,值最小。因此,金属在靠近接收线圈的位置或者发射线圈时探测灵敏度较高,在中间灵敏度最小。

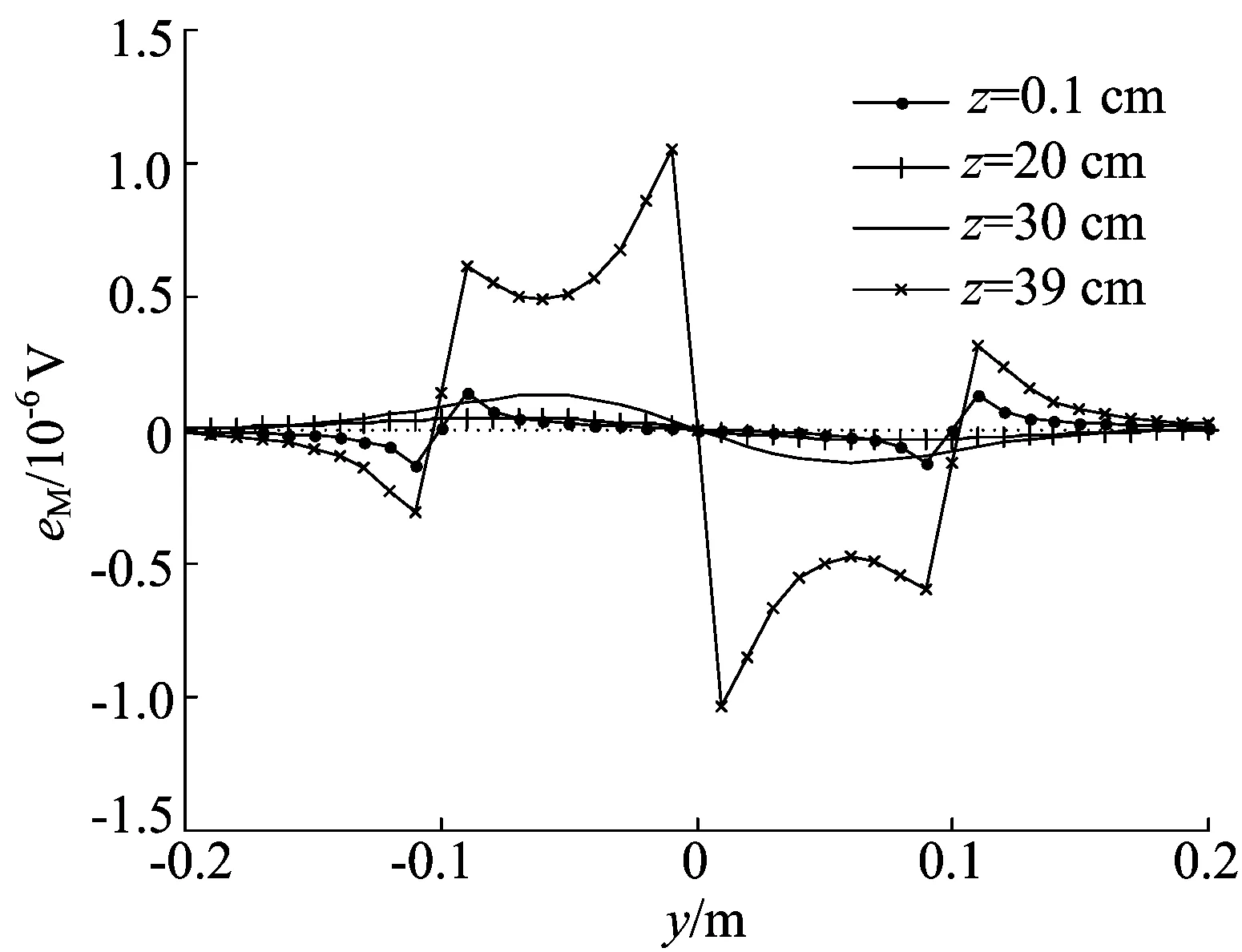
图3　金属的垂直位置对感应电动势的影响

3.3　线圈尺寸比例对探测结果的影响

将矩形线圈的长边分别是短边的1倍、2倍、3倍、4倍作为具体模型,将线圈等效为2条无限长的直导线的情况下作为理想模型,分析z等于1 cm时具体模型和理想模型中发射线圈在空间产生的磁场的变化情况,如图4所示。

由图4可以看出:当矩形线圈的长边是短边的4倍时,可以将线圈等效为2条无限长的直导线,此时将传感器模型等效为理想模型。因此当矩形线圈的长边是短边的4倍以上时,传感器的探测精度比较高,同时为了有较小尺寸,所以矩形线圈的长边为短边的4倍。

图4　4种线圈尺寸比例的不同结果

4实验验证

为了验证理论分析的正确性,选取金属异物的半径为6 mm的不锈钢螺母和半径为5 mm的铜螺母,测量不同金属在传感器的不同位置上电动势幅值的变化,结果如图5所示。

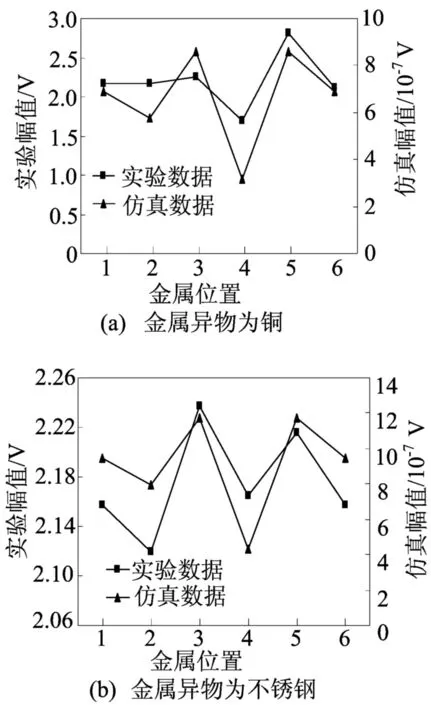
图5　仿真结果与实验结果对比

因为实验数据是通过放大电路测量出来的，致使其与仿真数据相差若干数量级。由图5可知金属异物感应电动势的幅值随位置交替变化,而且铜的幅值大于不锈钢。实验结果与仿真结果的变化趋势基本一致,从而验证了模型和算法的正确性。

5结束语

本文基于开放式矩形平衡线圈检测模型对金属探测仪的探测性能进行了分析,推导出了感应电动势的解析表达式,讨论了金属探测位置以及线圈尺寸比例对结果的不同影响,得到了最佳金属探测位置和线圈尺寸比例,最后通过实验验证了理论分析的正确性,从而为合理选择线圈尺寸比例和金属最佳探测位置提供了理论依据,为进一步提高金属探测仪的检测灵敏度和稳定性奠定了基础。

[参考文献]

[1]王庆林.基于平衡线圈技术的金属探测器设计[D].济南:山东大学,2010.

[2]Yamazaki S,Nakane H,Member S,et al.Basic Analysis of a Metal Detector[J].IEEE Trans Instrum Meas,2002,51(4):810-814.

[3]Butlek T.Metal detection testing provides protection for consumers and machinery.Sens Rev,1991.

[4]于晓洋.电涡流式金属异物检测系统的研究[J]. 仪器仪表学报,1995,16(1):95-98.

[5]黄勇.金属探测器的研究与设计[D]. 广州:华南理工大学,2010.

[6]苏庆丰,李智,牛军浩.金属探测器的平衡式线圈最佳空间位置研究[J].国外电子测量技术,2010,29(3):20-22.

[7]冯慈璋.电磁场[M].北京:人民教育出版社,1979:123-157，293.

[8]邝向军.矩形载流线圈的空间磁场计算[J].四川理工学院学报:自然科学版,2006,19(1):17-20.

[9]黎泽伦,孟杰,黄友均,等.多注行波管PPM聚焦系统横向磁场研究[J].合肥工业大学学报:自然科学版,2014,37(1):73-77.

[10]强锡富.传感器[M]. 北京:机械工业出版社,1989:91-99.

(责任编辑何晓雄)

宋开宏(1969-),男,安徽芜湖人,安徽大学副教授,硕士生导师.

Characteristic analysis of metal detector sensor based on open coil system

WANG Ru-ru,SONG Kai-hong,MING Jun,PAN Yu-tian,WU Zhen-fei

(School of Electronics and Information Engineering, Anhui University, Hefei 230601, China)

Abstract:Based on the open rectangular balanced coil model to deal with the lack of theory analysis for the design of metal detector sensor, the additional induced electromotive force when metal impurities go through the balanced coil is inferred. The best size ratio of the sensor coil and the best spatial detection position when metallic materials go through the balanced coil are obtained by the simulation analysis. The correctness of the proposed method is confirmed by experiments, thus providing a theoretical basis for improving the detection precision and stability of metal detector.

Key words:metal detector; sensor; rectangular balanced coil; induced electromotive force; spatial location

中图分类号:TM154.1

文献标识码：A

文章编号：1003-5060(2015)03-0354-04

doi:10.3969/j.issn.1003-5060.2015.03.014

作者简介：王茹茹(1987-),女,安徽淮南人,安徽大学硕士生；

基金项目：安徽大学研究生学术创新研究资助项目(10117700501)；安徽大学科研训练计划资助项目(kyxl2013031)

收稿日期：2014-01-07；修回日期：2014-03-26