一种下肢康复机器人机构及匀速训练方法的研究

伍保华,　王　勇

(合肥工业大学 机械与汽车工程学院, 安徽 合肥　230009)



一种下肢康复机器人机构及匀速训练方法的研究

伍保华,王勇

(合肥工业大学 机械与汽车工程学院, 安徽 合肥230009)

摘要:针对下肢具有功能障碍的偏瘫或残疾患者,文章研制了基于五杆并联机构的新型坐式下肢康复机器人，建立了患者下肢与康复训练机构的人-机参数化模型,并利用闭环矢量法对模型进行运动学正、逆分析,推导出其运动学方程。根据运动学分析并利用Matlab进行编程,分段拟合得到匀速训练下曲柄角速度与时间的函数,并在Pro/E软件中进行验证,仿真数据表明该函数和运动学分析结果是正确的。

关键词:康复机器人;五杆机构;运动学分析;匀速训练;Matlab软件;仿真分析

0引言

在我国,每年因意外事故、疾病和机体老化等因素造成肢体功能障碍或残疾的患者日益增多,可见在中国发展康复事业的重要性和紧迫性[1]。临床实践证明,对患者的偏瘫肢体进行科学康复训练,可以补偿和恢复肢体失去的功能,改善患者的生活自理能力,提高其生活质量[2]。在国外,许多科研工作者和医疗机构都开展了康复机器人的相关研究,并取得了一些有价值的研究成果[3-4]。在国内,对康复机器人的研究也取得一定的成果[5-6]。为克服目前康复机器训练机器人的不足[7]和适应患者的不同身高、同一患者在不同的康复时期的训练需求,设计了一款轨迹可变、幅度可调的坐式下肢康复机器人。患者在康复过程中,匀速训练[8]能避免因腿部速度波动较大造成的肌肉二次损伤。因此,研究康复机器人实现患者下肢匀速摆动训练的方法具有重大意义。

1坐式下肢康复机器人

坐式下肢康复机器人的简图如图1所示,康复机器人主要设计原理是采用能够精确地实现给定的任意复杂轨迹2DOF平面五杆机构[9]作为下肢训练机构，从而满足患者训练要求。

图1　坐式下肢康复机器人简图

在座椅的两侧对称布置了左右下肢训练装置,曲柄通过调节装置可以实现长度变化,辅助杆与机架水平夹角可以通过动力机构来调节其大小。根据患者的实际需求将曲柄调整到合适长度、辅助杆调整到合适位置时,五杆机构转换为四杆机构,进行康复训练。康复机器人还设定了主动模式和被动模式,被动模式是指曲柄以角速度w转动,带动患者下肢做康复训练。主动模式是指大腿作为动力源,带动训练机构,通过调整训练机构中的阻力装置,来达到训练康复目的。主动和被动模式的设定以及机构的可调节性,满足了患者的个性化康复训练需求。

在实现患者下肢匀速摆动方法研究中,首先应根据患者实际情况,得出患者下肢关节活动度与时间函数,然后进行运动学逆分析,通过Matlab编程得出曲柄角速度与时间的运动学方程,再进行运动学正分析,通过Pro/E软件仿真验证运动方程的正确性,因此,建立机构的运动学方程十分必要。

2运动学正分析

在训练过程中,患者的下肢通过一个固定装置使得其小腿及踝关节固连,保证了左右下肢在一个平面内运动。人体下肢结构可以用平面二杆机构模拟,使康复机器人训练机构与患者下肢一起构成了平面七杆机构，因此,可以采用闭环矢量法进行运动学分析。机构模型如图2所示,以过髋关节的铅垂线建立Y轴,以过辅助杆与机架的转动副中心的水平线建立X轴,建立坐标系XOY,已知参数为l0、l1、l2、l3、l4、l5、l6、l7、l8、l9,辅助杆4与机架水平方向的夹角β决定C点的运动轨迹位置和幅度,在每个工作位置,β是固定不变的,其有效调整范围为-90°～10°。运动学正分析就是已知原动件转角θ1变化规律,求解C点位置、速度及θ7、θ8,即膝关节转角和髋关节转角运动规律。

图2　机构模型

2.1　位移正分析

在闭环OFEDHG中有:

(1)

即

(2)

其中,θ0、θ4为常量,θ3=0°,利用欧拉公式eiθ=cosθ+isinθ将(2)式展开,取实部整理可得:

l5cosθ5=l0cosθ0+l1cosθ1+

l5sinθ5=l0sinθ0+l1sinθ1+

(3)

令a=l0cosθ0,b=l0sinθ0,c=l4cosθ4,d=l4cosθ4,消去θ5,整理得:

Acosθ2+Bsinθ2+C=0

(4)

其中，

A=2al2-2cl2-2l2l3+2l1l2cosθ1;

B=2bl2-2dl2+2l1l2sinθ1；

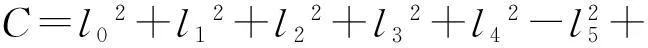
(2bl1-2dl1)sinθ1+(2al1-2cl1-

2l1l3)cosθ1+2cl3-2bd-2al3-2ac。

解得:

将θ2代入(3)式可解出θ5。

在闭环OFECBA中有:

(5)

即

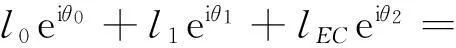
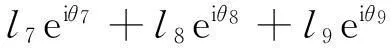
(6)

其中，θ0为常量；θ2已经求出；θ9=90°。

令m=lECcosθ2,n=lECsinθ2，利用欧拉公式将(6)式展开,取实部整理可得方程组：

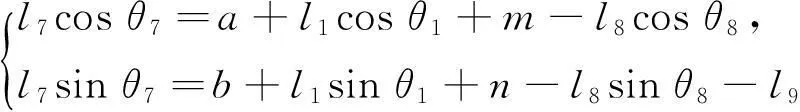
(7)

整理得:

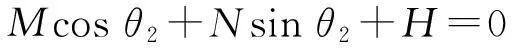
(8)

其中，

M=-2al8-2l8m-2l1l8cosθ1；

N=-2nl8-2l8b-2l1l8sinθ1；

(2l1m+2al1)cosθ1+(2bl1+2nl1-

2l1l9)sinθ1+2am-2bn-2bl9-2nl9。

解得:

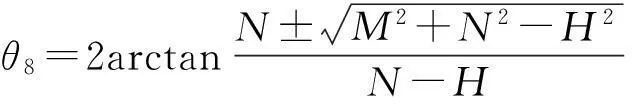
(9)

将θ8代入(7)式,可解得:

θ7=arcsin[(b+l1sinθ1+n-

(10)

根据以上位移正分析得髋关节转角φ1、膝关节转角φ2、C点位置(xC、yC),结合图2可得:

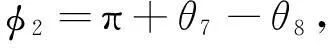
xC=a+m+l1cosθ1，

yC=b-n+l1sinθ1

(11)

2.2　速度正分析

将(2)式两边同时对时间t求导可得:

l1iw1eiθ1+l2iw2eiθ2=l5iw5eiθ5

(12)

(12)式利用欧拉公式展开取实部得:

(13)

将(13)式代入(12)式可解w5。将(6)式两边同时对时间t求导可得:

l1iw1eiθ1+lECiw2eiθ2=l8iw8eiθ8+l7iw7eiθ7

(14)

(14)式利用欧拉公式展开取实部得:

(15)

同理可解出w8为：

(16)

根据以上速度正分析可得出:

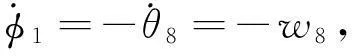
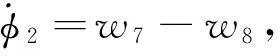
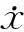
(17)

3运动学逆分析

3.1　位移逆分析

由(7)式可得：

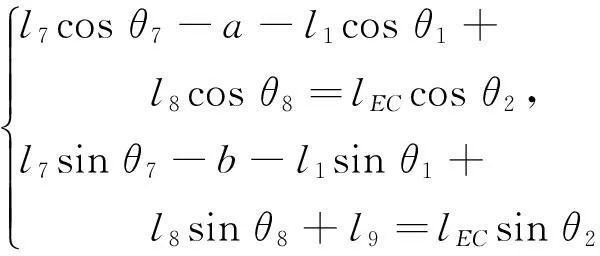
(18)

整理得:

Kcosθ1+Jsinθ1+G=0

(19)

可解出曲柄角度为:

(20)

其中,

K=2al1-2l1l7cosθ7-2l1l8cosθ8;

J=2bl1-2l1l7sinθ7-2l1l8sinθ8-2l1l9;

G=l02+l12+l72+l92-lEC2-2bl9-

(2bl7+2l7l9)sinθ7+(2l8l9-2bl8)sinθ8-

2al7cosθ7-2al8cosθ8+2l7l8cos(θ7-θ8)。

将(20)式代入(18)式即可求解出θ2。

3.2　速度逆分析

由(14)式两边同时乘以e-iθ2,利用欧拉公式展开取实部得:

(21)

将(21)式代入(13)式可解w2。

由于坐式下肢康复机器人左右两套对称训练机构关于人体的矢状面[10]对称,因此,只要对右下肢人-机训练机构分析,通过几何关系和位置关系换算可以得出左下肢人-机训练机构参数。

4仿真分析

图2中A、B、C分别表示髋关节、膝关节、踝关节中心点；E、F、G、H、D分别为训练机构回转副的中心点,图示相关角度定义逆时针为正。以身高l=1 700 mm患者为例,取l0=0.159l,l1=0.056l,l2=0.182l,l3=0.111l,l4=0.085l,l5=0.206l,l6=0.147l,l7=0.250l,l8=0.282l,l9=0.183l,采用Pro/E仿真软件建立患者下肢-训练机构参数化模型进行仿真分析。

4.1　建立大腿等速摆动下曲柄角速度运动方程

由试验可得,坐姿状态下正常人体关节活动度在矢状面范围大致为:大腿与椅面夹角摆幅为-10°～70°,即髋关节活动度；大腿与小腿夹角活动幅度为20°～180°,即膝关节活动度。在实际康复训练中,偏瘫患者下肢会出现肌肉痉挛现象,下肢的变化角度如果超过了患者的承受能力或者下肢的变化角度速度过大突变,会导致患者的肢体产生二次损伤,所以患者下肢的变化夹角一定要比正常人小。

考虑患者在康复过程中各关节的舒适性以及训练机构的连续性,患者下肢在训练过程中,可取φ1为0°～60°,φ2为30°～170°。经试验发现,大腿患者大腿与椅面的夹角大约在3.2 s来回匀速摆动1次,训练效果较佳。为减少大腿一个周期内摆动换向时的过大冲击,进行分段处理，当t为0～1.6 s时,实现大腿从椅面摆动到最高点；当t为1.6～3.2 s时,实现腿部从最高点摆动到椅面。2个过程的大腿都是先匀加速再等速,最后匀减速到0,摆动情况相同,可将φ1与t的关系写成如下函数:

时间t为1.6～3.2 s时,运动过程与之相同。对φ2的处理与φ1相同,将φ1、φ2函数关系与相关实验参数代入(11)式,并利用运动学逆分析方程(16)式、(20)式在Matlab中进行编程并进行绘图,可以得出匀速摆动训练下,曲柄角速度运动规律与时间的关系,并用10次多项式进行拟合,得到t为0~1.6 s时曲柄转动1周角速度方程w1如下：

w1=36 215.135 5t10-279 552.535 4t9+

923 265.29t8-1 705 970.786 3t7+

1 937 162.637 7t6-1 399 780.087 3t5+

646 026.217 7t4-186 733.596 8t3+

32 156.050 5t2-2 831.054 2t-

2.500 8，0≤t≤1.6。

当t为0~1.6 s时,曲柄角速度运动规律与时间的关系及其拟合曲线如图3a所示。对曲线进行积分,可以得出时间在t为0~1.6 s时,曲柄转过的角度θ1为0°～-121.5°。

同理可以得出t为1.6～3.2 s时,曲柄角速度方程如下：

w1=25 624.266 3t10-622 876.821 1t9+

6 781 266.129 8t8-43 539 004.971 5t7+

182 549 184.627 4t6-522 221 467.509 4t5+

1 032 209 266.166 3t4-1 391 873 892.834 4t3+

1 225 341 418.585 3t2-635 931 768.894 1t+

147 741 932.049 1，1.6

t为1.6~3.2 s时曲柄角速度运动规律与时间的关系及其拟合曲线如图3b所示。

图3　原动件运动规律曲线

对曲线进行积分,可以得出时间t在1.6~3.2 s内,曲柄转过的角度θ1为-121.5°～-360°。

4.2　仿真验证

在仿真过程中,设定曲柄以3.2 s为1个转动周期,此时患者下肢实现来回摆动1次。分别让曲柄在等角速度转动下和输入本文建立的曲柄角速度w1方程2种情况下进行仿真,分别得出患者下肢髋关节转角位置、角速度与时间的关系,如图4所示。

从图4a可以看出,曲柄以等角速度转动1周时,大腿来回摆动的2个过程用时不同,运动状态不同,而曲柄以w1运转1周,大腿来回摆动用时相同,运动过程也相同,这使得患者下肢在1个周期内受力更均匀,有利于提高康复训练效果。

图4　曲柄在不同角速度下髋关节转角位置和角速度

5结束语

本文建立了坐式下肢康复机器人的人-机系统正、逆运动学方程,根据运动学分析并通过Matlab进行编程,分段拟合得到了使患者下肢匀速训练曲柄角速度与时间的函数w1,利用Pro/E仿真验证了曲柄在w1转动下,患者下肢能实现匀速训练，并为坐式下肢康复机器人的机构控制提供一种方法。

[参考文献]

[1]Jeffrey A W,Sivakumar B,Thomas S.Bobotic gait trainer reliability and stroker patient case study[C]//10th International Conference on Rehabilitation Robotics,2007:554-561.

[2]吕广明,孙立宁,彭龙刚.康复机器人技术发展现状及关键技术分析[J].哈尔滨工业大学学报,2004,36(9):1224-1227.

[3]Senanayake C.Emerging robotics devices for therapeutic rehabilitation of the lower extremity[C]//IEEE International Conference on Advanced Intelligent Mechatronics,2009:1142-1147.

[4]Simon A M,Gillespie R B,Ferris D P.Symmetry-based resistance as a novel means of lower limb rehabilitation [J].Journal of Biomechanics,2007,40(6):1286-1292.

[5]张立勋.卧式下肢康复机器人运动学分析及仿真[J].系统仿真学报,2010,22(8):2001-2005.

[6]朱建瓴,刘成良.人体下肢康复机构设计及运动学仿真[J]. 计算机仿真,2007,24(3):145-148.

[7]王勇,张英,刘正士,等.下肢康复机器人的设计与仿真分析[J].华中科技大学学报:自然科学版,2011, 39(Z2):252-254.

[8]吴毅,杨晓冰,李云霞,等.等速肌力训练促进膝关节术后肌力恢复的研究[J].中国康复医学杂志,1994,9(5):193-197.

[9]于红英,唐德威.平面二自由度全铰链五杆机构轨迹机构综合方法的研究[J].机械科学与技术,2006,25(7):852-855.

[10]朱序璋.人机工程学[M].西安: 西安电子科技大学出版社,1999:13-20.

(责任编辑闫杏丽)

王勇(1969-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师.

Study of uniform training methods and mechanism for a lower limb rehabilitation robot

WU Bao-hua,WANG Yong

(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:A new model for sitting lower limbs rehabilitation robot was developed based on the new five-bar parallel mechanism, aiming at hemiplegia or disabled patients with lower extremity dysfunction. The man-machine parametric model was established in patients with lower limb and rehabilitation training institutions. The direct and inverse kinematics of the model was analyzed using the closed-loop vector method and the kinematics equation was deduced. Through the kinematics analysis and the programming using Matlab software, a function of the crank angular velocity and time was obtained by segmented fitting, and it was verified by Pro/E software. The simulation result indicates that the function and kinematics analysis are correct.

Key words:rehabilitation robot; five-bar mechanism; kinematics analysis; uniform training; Matlab software; simulation analysis

中图分类号:TP242

文献标识码：A

文章编号：1003-5060(2015)03-0295-05

doi:10.3969/j.issn.1003-5060.2015.03.002

作者简介：伍保华(1989-),男,湖南衡阳人,合肥工业大学硕士生；

基金项目：科技部创新基金资助项目(11C26213402042)

收稿日期：2014-03-14；修回日期：2014-04-11