两轮智能车跟踪控制系统的研究

陈　梅,　陈艳燕

(合肥工业大学 电气与自动化工程学院,安徽 合肥　230009)



两轮智能车跟踪控制系统的研究

陈梅,陈艳燕

(合肥工业大学 电气与自动化工程学院,安徽 合肥230009)

摘要:自平衡式两轮机器人是多变量、强耦合对象,文章针对斜坡上的两轮智能车的目标跟踪问题,设计了基于T-S模糊控制器的跟踪控制系统,该系统包括底层平衡控制器、底层转弯控制器和全局运动控制器。底层的平衡控制应用T-S模糊控制器,并利用LQR线性控制器来简化控制器的参数设计。底层转弯控制器采用PI算法,在此基础上运用李雅普诺夫函数方法,进行了全局运动控制器的设计,得出了具有全局渐近稳定的控制律。最后通过仿真验证了该方法的正确性和可行性。

关键词:机器人;模糊控制;两轮智能车;目标跟踪

0引言

近年来,随着移动机器人的研究不断深入，其应用领域更加广泛,所面临的环境和任务也越来越复杂,两轮智能车越来越受关注。对于两轮智能车目标跟踪问题,其跟踪控制系统是至关重要的一环。就单个小车而言,小车的跟踪控制可分为全局运动控制和底层运动控制2部分。全局运动控制包括轨迹规划与生成2部分,决定了小车该如何运动,包括平动和转动。底层运动控制的根本任务是实现小车接收到的期望速度,这最终是通过调整电机转矩以调节轮子转速实现的。

对于运动控制问题,大多文献中采用的稳定算法都是李雅普诺夫理论、反馈线性化等[1],然而由于采用的是线性化后的模型,忽略了许多不确定参数,而且模型与实际中非线性系统也存在差异,应用于真实系统时需要增添鲁棒性的控制。文献[2]采用全状态反馈线性控制器,但线性控制器的鲁棒性具有局限性。

本文采用T-S模糊控制器来设计底层运动控制器,相对于经典PID控制系统具有较强鲁棒性,对于控制器的参数利用LQR线性控制器来简化设计,相对于其他智能控制器具有参数调整简单方便的特点。另外在底层运动控制器基础上,采用控制Lyapunov函数方法进行了全局运动控制器的设计,由于是在非线性模型基础上设计的,因而减小了与真实系统的差异性,能有效地实现两轮智能车的目标跟踪控制,保证了系统运动的稳定性。

考虑到现实情况中地面总有凹凸不平,因而小车在斜坡上的模型更为合适,为了进一步设计非线性控制器,需要对小车在斜坡上的情况进行建模。建立了非线性模型之后,应用模糊逻辑控制方法设计底层运动控制器,并通过LQR控制器来简化模糊控制器的参数设计。另外,为了进一步设计全局运动控制器,需要先设计转弯控制器,本文采用PI控制器来设计转弯控制器,运用李雅普诺夫函数方法设计控制算法,全局运动控制器最终完成了两轮智能车的目标跟踪控制,最后用仿真和实验加以验证。

1两轮智能车的建模

1.1　动力学模型的建立

两轮智能车在角度为φ的斜坡上的模型如图1所示,其中,θp为车体与竖直方向y轴的夹角;R车为车轮的半径;D为两车轮间距;L为车体(不包括车轮)质心到z轴的距离;δ为车体绕y轴旋转角度;M为车体质量(包括车箱、摆杆);m、JR分别为左右车轮质量和转动惯量;Jpθ为车体绕通过质心且平行于z轴的轴的转动惯量;Jpδ为车体绕y轴的转动惯量。

图1　系统模型

采用拉格朗日方程建立系统数学模型,首先分析系统的约束类型和主动力性质,判定是否符合拉格朗日方程的条件;其次判定系统的自由度,选取适当的广义坐标;最后写出系统的动能T、势能和拉格朗日函数L,并得出系统的数学模型[3-4]。

选左轮转角θ1、右轮转角θ2和智能车体质心在x-y平面内的转角θp为运动状态变量,此时系统具有完整约束,因此,选用θ1、θ2、θp作为系统的3个广义坐标,在此坐标系下广义力分别为电机对左轮转矩C1、电机对右轮转矩C2和车体与电机对车体作用的转矩MgLsinθp-C1-C2。

系统动能包括:

其中,T1为左右车轮的平动动能与车轮绕y轴转动动能;T2为左右车轮绕转z轴的转动动能T;T3为车体质心的沿斜坡动能;T4为车体绕通过质心且平行于z轴的轴的转动动能;T5为车体绕垂直方向轴的转动动能;T6为左右轮和车体的势能。

根据拉格朗日函数以及系统的8个约束条件,整理得出:

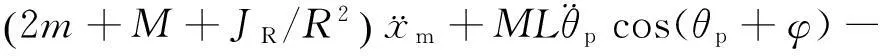
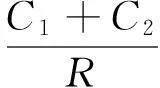
(1)

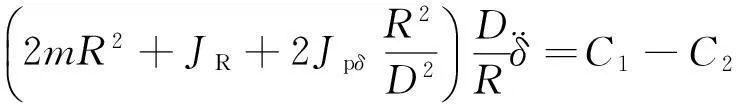
(2)

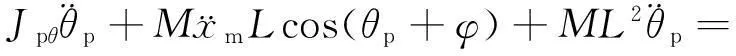
MgLsinθp-(C1+C2)

(3)

通过以上公式,完成了两轮智能车在斜坡上的建模,由此可以进一步进行控制器的设计,这也是设计控制系统的理论基础。

1.2　目标跟踪模型的建立

设小车初始状态(x,y,δ)为(0,0,0),目标初始状态也为(0,0,0)。小车与运动目标点关系图如图2所示。

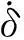
(4)

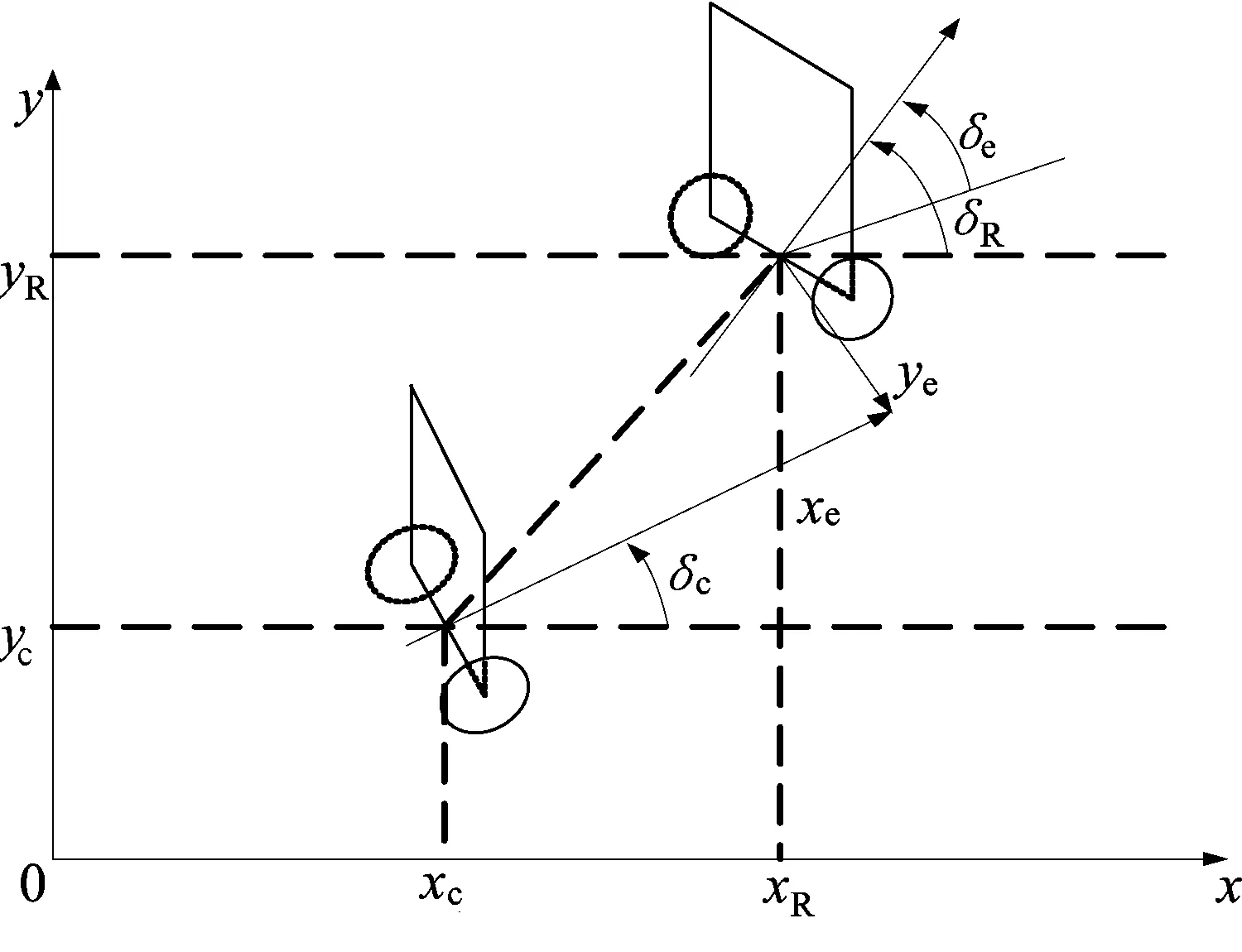
图2　小车与运动目标点关系图

由图2所示的几何关系,位姿误差矢量Pe可描述为:

(5)

对(5)式求导可得到目标跟踪误差微分方程:

(6)

2底层平衡控制器的设计

小车的平衡控制器部分采用T-S型模糊逻辑控制器,4个输入,对每个输入用{负,正}2个语言变量来表示,为了书写方便还可以表示为{N,P}。取模糊集的隶属度函数为“S形”和“Z形”隶属度函数,对于控制器的输出采用固定值,由此一共有24=16条模糊规则[5-6]。

2.1　模糊控制规则的建立

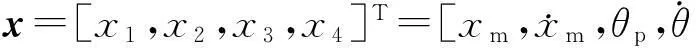
由于“Z形”和“S形”很适合于表达负(N)与正(P)语言变量,其表达式都为二阶多项式,便于运算,且其增益的变化适用于小车的控制,因而采用其作为控制器4个输入的隶属度函数,如图3所示,图3中mi(i=1,2,3,4)的选取与实际中各个状态量有关。

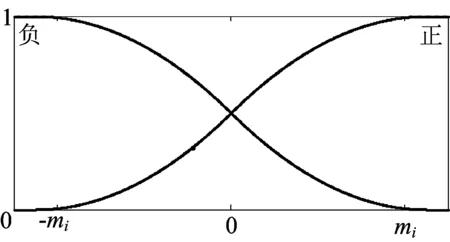
图3　隶属度函数曲线图

选取16种最特殊的情形,输出为特定转矩τ1～τ16,即当各输入量为m1、m2、m3、m4时,输出量为τ1;各输入量为m1、-m2、m3、m4时,输出量为τ2,以此类推。当2条规则的输入互补时,输出控制量大小一样,而方向相反,即τ1=-τ16,τ2=-τ15,…，由此需根据8种最特殊的情形确定n1～n8,从而确定完整的规则表，见表1所列。

表1　模糊控制规则表

2.2　输出参数的确定

模糊推理系统的编辑包括输入输出隶属度函数的编辑、模糊规则的编辑、模糊推理过程合成隶属度方法的选取以及去模糊化方法的选择等。本文的模糊推理规则采用积运算合成条件隶属度,去模糊化采用离散重心法。

由此可得出模糊控制器的输出为16条规则的加权平均结果,第1条规则的权系数为:

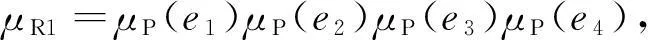
则模糊控制器的输出为:

(7)

输出参数的调整对于控制器的控制效果具有直接的效果,在16条规则中,当输入对称地相反时,输出控制量大小一样,而方向相反,如τ1与τ16,τ2与τ15,…，因而一共需确定8个参数,即n1～n8。对于此8个参数的确定,可以采用LQR控制器来简化。因为模糊控制器的效果,其实是相当于比例系数变化的LQR控制器,即对于(7)式,可表示为:

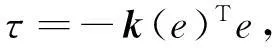
则可设计LQR控制器为:

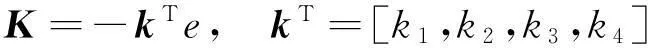
(8)

可看出当4个输入都为正限值时,控制器输出为:

τ1=n1=-k1m1-k2m2-k3m3-k4m4。

当4个输入为m1、-m2、m3、m4时,控制器输出为:

τ2=n2=-k1m1+k2m2-k3m3-k4m4。

由此可看出,只需要确定了LQR控制器的4个参数,就可以确定模糊控制器的输出参数。

3全局运动控制器的设计

要实现小车的跟踪控制,首先要进行小车实时位置计算[7]。设小车的初始位置及角度为(δ0,x0,y0)。经过一个步长Δt,小车的位置及角度为(δΔt,xΔt,yΔt)，计算公式如下：

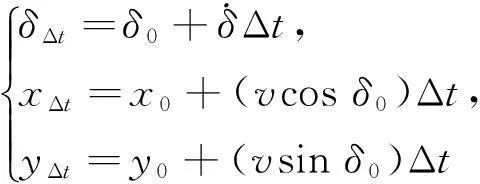
(9)

再将δΔt、xΔt、yΔt分别赋给δ0、x0、y0,由此计算小车位置,根据目标位置,得到小车与目标位置的距离以及与目标位置的方向偏差。

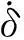
图4　小车总控制框图

图4中,解耦模块将小车的平衡与转弯总转矩分解到左右两轮,即左右轮各自的目标转矩可由(10)式得到:

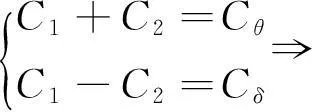
(10)

其控制流程步骤如下:

(1) 根据位移和旋转角度可以算出小车在参考系下的坐标(xc,yc)和前进方向δc。

(2) 根据小车位置和目标位置,计算目标相对于小车的距离ρ,以及目标对于小车的位置角度δR。

(3) 根据δR和δc计算小车行驶方向需要修正的角度δe。

(4) 根据设计的跟踪控制器,由δe和ρ计算小车速度控制量和旋转角速度控制量。

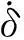
采用李雅普诺夫第二法,由于直角坐标系下运动模型有3个状态[xe,ye,δe]T,其中δe∈[0, 2π),因而选定正定的标量函数:

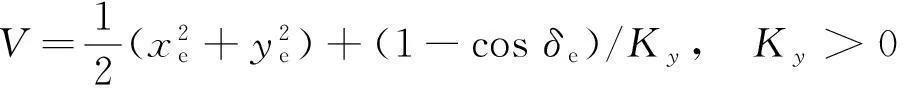
(11)

如果Pe=0,V=0;如果Pe≠0,V>0。

作为Lyapunov函数,在任意初始状态下,V对时间导数为:

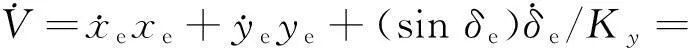
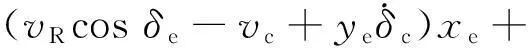
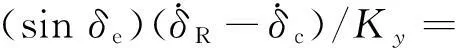
xe(vRcosδe-vc)+

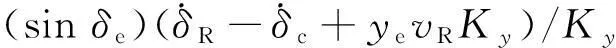
(12)

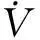
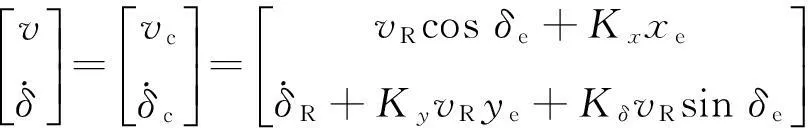
(13)

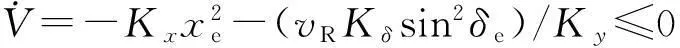
另外,对于全局运动控制器的速度输出进行限幅在0.6 m/s之内,以保证底层平衡控制器的各状态量在误差范围之内[9-10]。

4仿真与结果分析

小车模型参数见表2所列。

表2　系统模型参数

根据表2模型参数及T-S模糊控制器中各输入量取值,假设平衡子系统初始状态为[000.030]。当取Q=[0.1000;0000;0010;0000],R=0.1时,可得:

k=[-10.638,-5.258 67,-70.676 4,-3.450 4]T。

经调整可得表1所需确定的参数如下:

n1=27.00,n2=23.44,n3=13.00,n4=13.44,

n5=23.19,n6=22.2,n7=13.5,n8=12.8。

后方小车在追踪目标时,作如下情况仿真。

(1) 当目标运动轨迹为y=3x,Pw=-100,Iw=-5,Kx=-1,Ky=7.7,Kδ=6时,动点跟踪仿真1如图5所示。动点跟踪1目标角度、实际角度如图6所示。

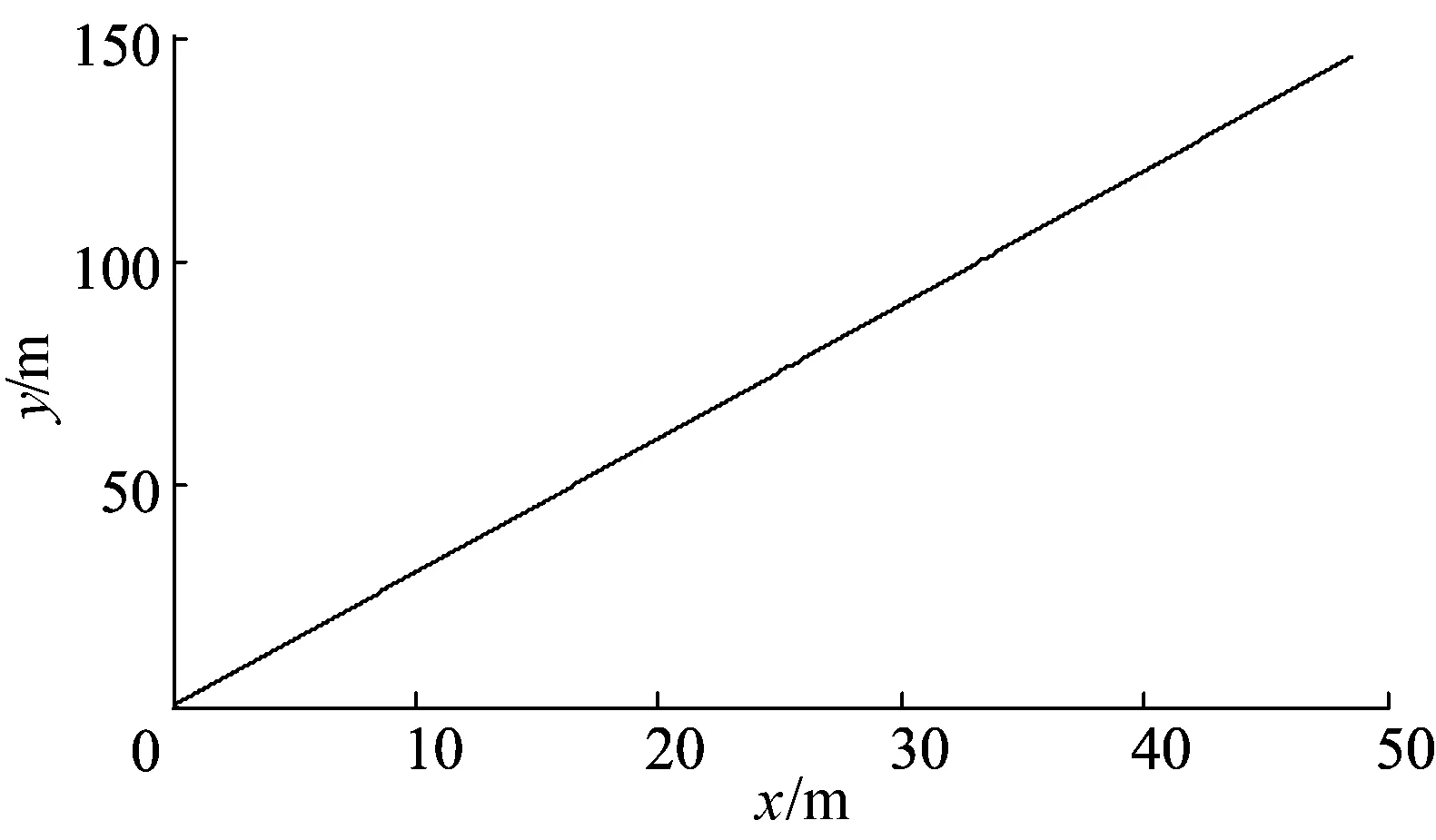
图5　动点跟踪仿真1

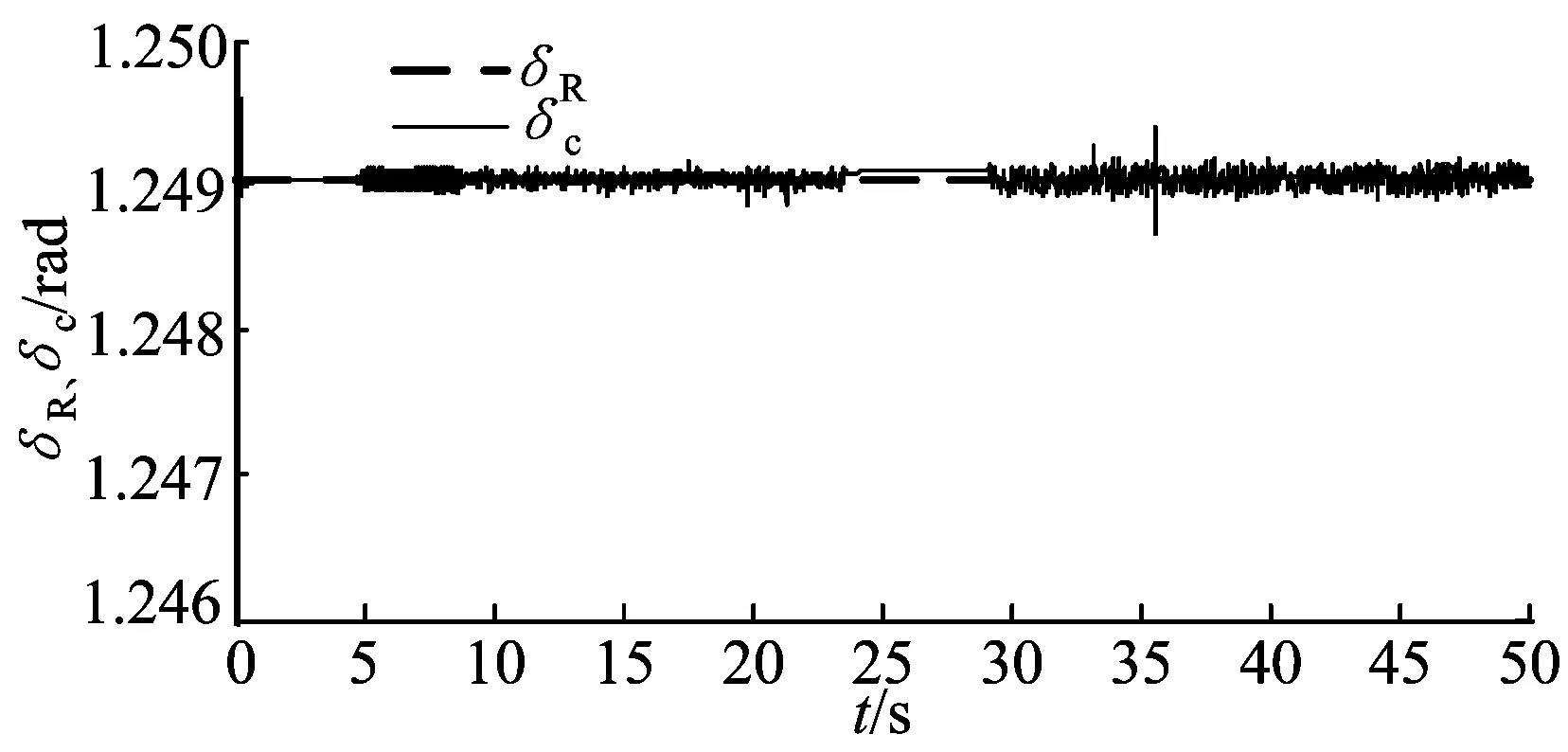
图6　动点跟踪1目标角度、实际角度

(2) 当目标运动轨迹为x2+y2=4,Pw=-100,Iw=-5,Kx=-1,Ky=10,Kδ=7时,动点跟踪仿真2如图7所示，动点跟踪2底层平衡控制器波形如图8所示，动点跟踪2底层转弯控制器波形如图9所示。

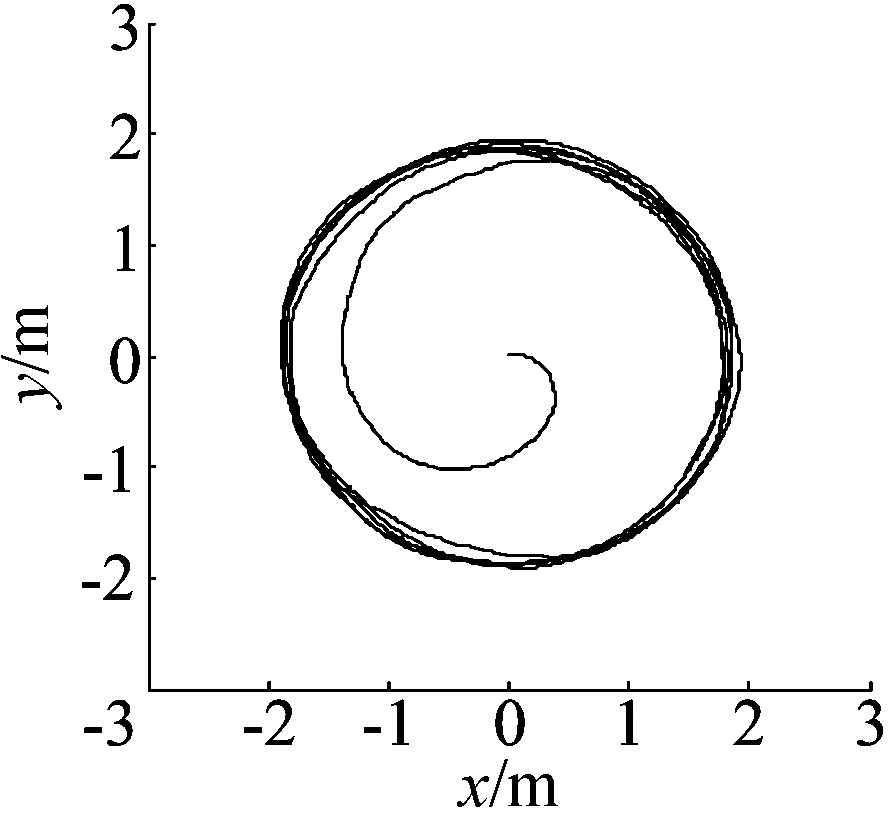
图7　动点跟踪仿真2

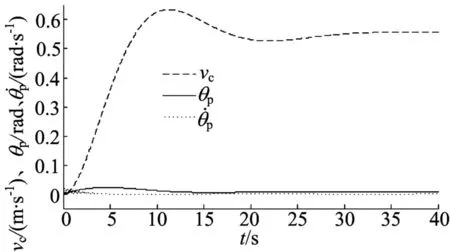
图8　动点跟踪2底层平衡控制器波形

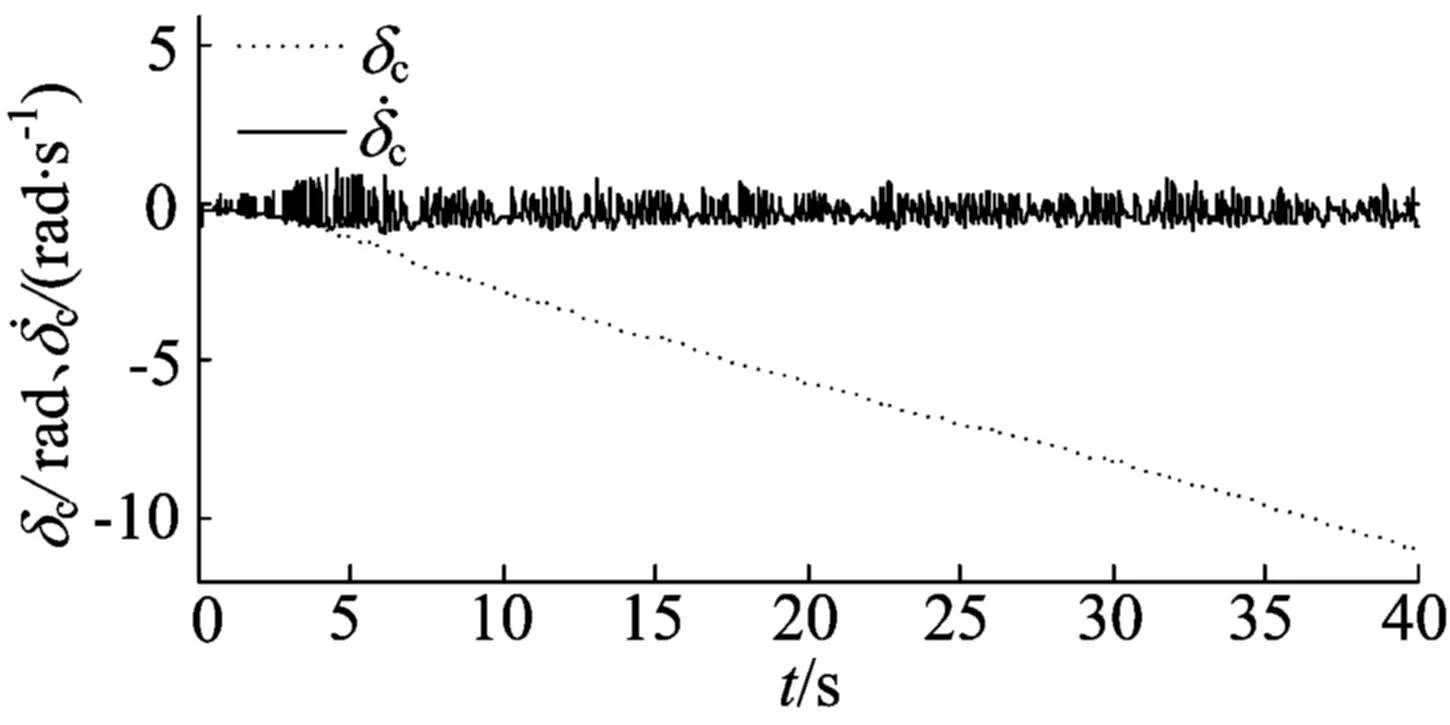
(a)　小车转弯角度、转弯角速度波形

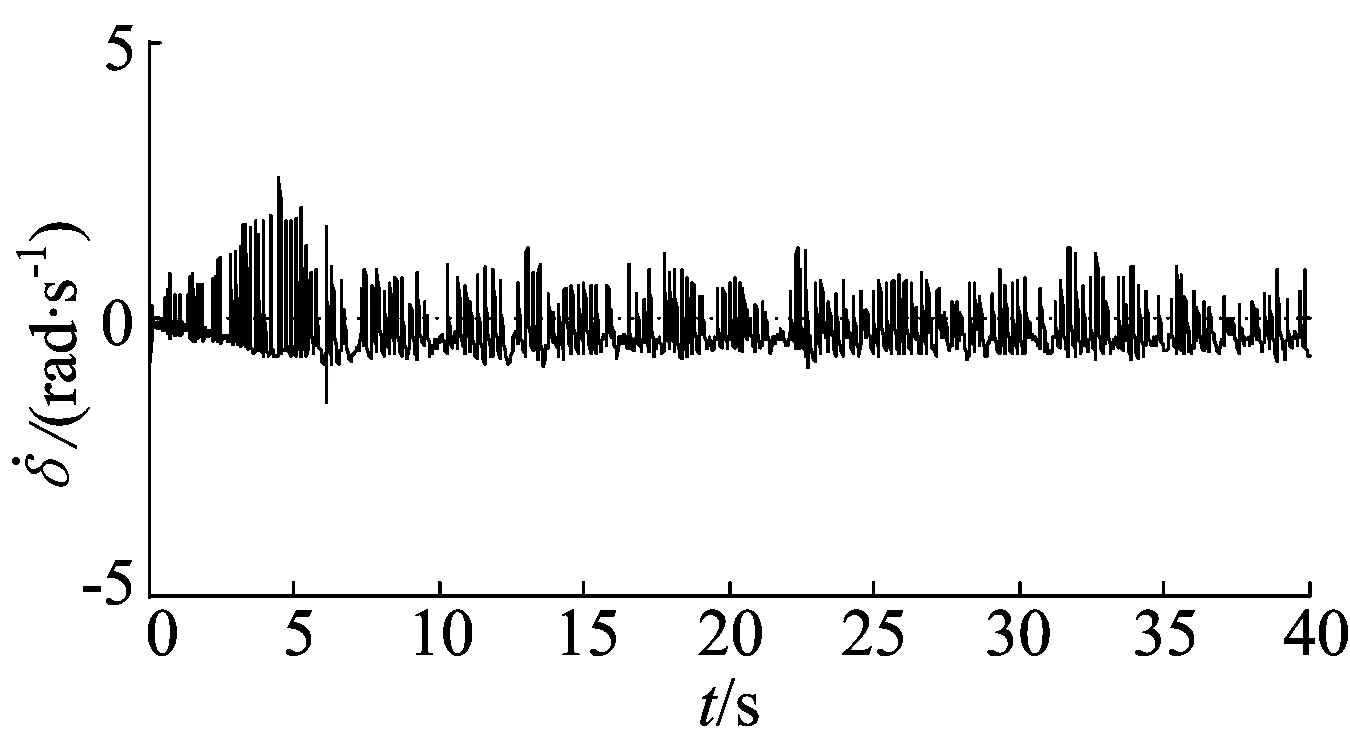
(b)　小车转弯角速度给定波形

(3) 将动点跟踪仿真2作为例子,在跟踪时刻4 s处,给小车车身加个5°左右的倾角扰动,进行抗扰动仿真,结果如图10～图12所示。

图10　干扰信号

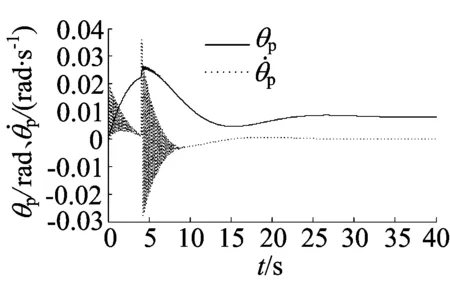
图11　干扰下底层平衡控制器波形

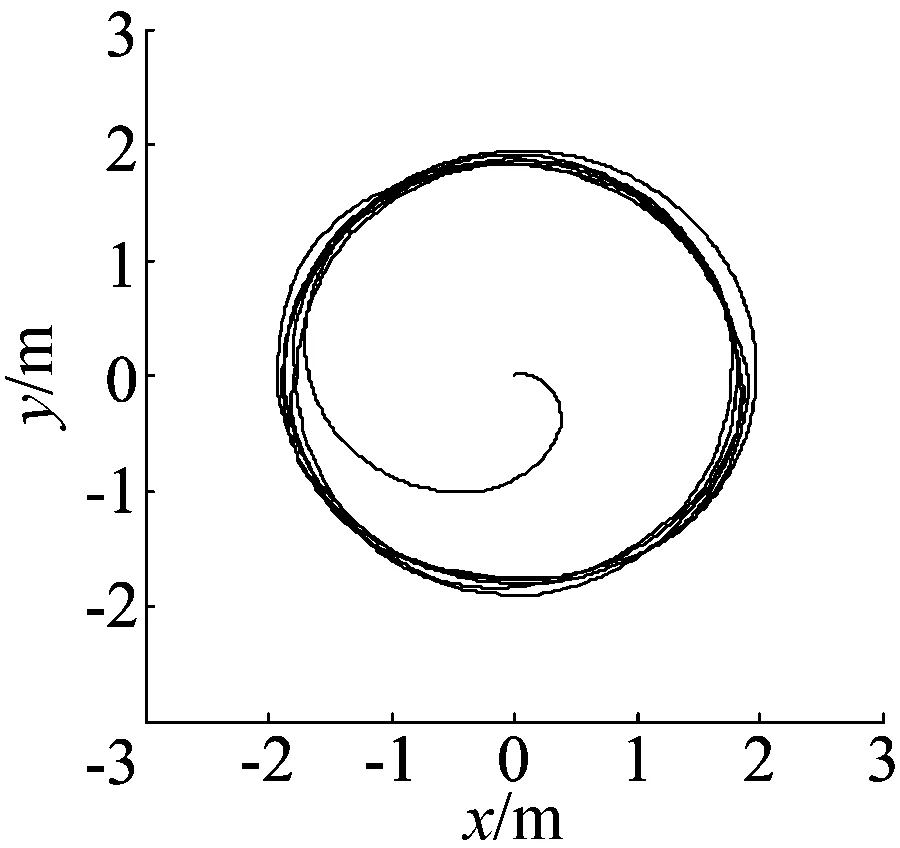
图12　干扰下动点跟踪仿真

小车成功跟踪运动目标运行期望轨迹。动点跟踪仿真1中小车起始角度为0°，朝向x轴,动点起始角度为71.56°,小车迅速调整角度,并根据全局运动控制器的计算跟踪动点,实际角度有微小的波动。

动点跟踪仿真2中小车起始点在原点,动点从(0,2)点开始顺时针以-1 rad/s角速度运动,小车跟踪时轨迹在小范围误差之内;根据全局运动控制器的计算,速度给定稳定在限幅值0.6 m/s,速度、倾角与倾角速度变化平稳，快速趋向稳定,且都在误差范围内;根据全局运动控制器的计算,转弯角速度给定在0.3 rad/s附近不断变化,而小车实际转弯角度与转弯角速度的波形响应快速,保证了小车追踪目标的准确度。

干扰仿真中,给小车车身一个力,使车身往倾斜方向再倾斜5°左右的量,这个力大致维持0.2 s左右,从图11中可以看出,由于底层模糊控制器的作用,车身快速从干扰状态恢复到稳态,小车的跟踪由于加了扰动,跟踪的半径在短时间之内增大,从图12的开始段可以看出,第1圈稍微有些偏离,但很快调整过来,使跟踪误差保持在较小范围之内,达到稳态,证明了底层平衡控制器的鲁棒性和有效性。

5结束语

本文针对小车的目标跟踪问题,设计了基于T-S模糊控制器的运动控制系统。该系统中采用T-S模糊控制器作为底层平衡控制器,利用LQR线性控制器辅助设计参数,具有鲁棒性强、参数易确定等优点;底层转弯控制器采用PI算法,结构简单;全局运动控制器运用李雅普诺夫函数方法,保证了运动系统的全局渐近稳定性和可靠性。仿真结果也充分验证了该控制器的有效性和正确性,对两轮智能车运动控制系统的研究具有一定的参考意义。

[参考文献]

[1]Spong M W. Partial feedback linearization of underactuated mechanical systems[C]//Intelligent Robots and Systems' 94.'Advanced Robotic Systems and the Real World', IROS'94. Proceedings of the IEEE/RSJ/GI International Conference on， IEEE, 1994, 1: 314-321.

[2]阮晓钢,任红格.两轮自平衡机器人动力学建模及其平衡控制[J]. 计算机应用研究, 2009, 26(1): 99-101.

[3]潘连顺,葛汝明.拉格朗日方程与电路系统[J].德州师专学报,1994,4(10):22-25.

[4]尚年.经典力学[M].上海:复旦大学出版社,1990:98-150.

[5]增圻,效祥.智能控制理论与技术[M]. 北京:清华大学出版社, 1997：50-150.

[6]Xu J X, Guo Z Q, Lee T H. Design and implementation of a Takagi-Sugeno-type fuzzy logic controller on a two-wheeled mobile robot[J]. Industrial Electronics, IEEE Transactions on, 2013, 60(12): 5717-5728.

[7]杨兴明,丁学明,张培仁,等.两轮移动式倒立摆的运动控制[J]. 合肥工业大学学报: 自然科学版, 2005, 28(11):1485-1488.

[8]黄永志, 陈卫东. 两轮移动机器人运动控制系统的设计与实现 [J]. 机器人, 2004, 26(1)：40-44.

[9]王孝武.现代控制理论基础[M].北京:机械工业出版社,2006:81-170.

[10]袁泽睿. 两轮自平衡机器人控制算法的研究 [D]. 哈尔滨: 哈尔滨工业大学, 2006.

(责任编辑张镅)

Study of tracking control system of two-wheeled intelligent vehicle

CHEN Mei,CHEN Yan-yan

(School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China)

Abstract:Self-balancing two-wheeled robot is a multivariable and strong coupling plant. In this paper, a tracking control system based on T-S fuzzy controller is designed to solve the target tracking problem of the plant on the slopes, including the local balance controller, turning controller, and global motion controller. T-S fuzzy controller is utilized to implement the bottom balance control with the help of linear LQR controller to simplify the design of parameters. Bottom turning controller is designed on the basis of PI algorithm. The global motion controller design employs Lyapunov function method based on bottom turning controller to come to a globally asymptotically stable control law. The simulation result verifies the correctness and feasibility of the method.

Key words:robot; fuzzy control; two-wheeled intelligent vehicle; target tracking

中图分类号:TP273

文献标识码：A

文章编号：1003-5060(2015)03-0319-07

doi:10.3969/j.issn.1003-5060.2015.03.007

作者简介：陈梅(1963-),女,安徽合肥人,合肥工业大学副教授,硕士生导师.

收稿日期：2014-04-09；修回日期：2014-07-11