基于波粒去噪的图像清晰化方法

赵明敏，　田　丽，　杜道昶，　包　伟，　陈　勇

(安徽工程大学 电气工程学院， 安徽 芜湖 241000)



基于波粒去噪的图像清晰化方法

赵明敏，田丽，杜道昶，包伟，陈勇

(安徽工程大学 电气工程学院， 安徽 芜湖 241000)

[摘要]为了应对雾天图像对比度低、能见度低的缺点，提出一种基于波粒重构的雾天图像清晰化方法。采用波粒重构对均衡化后雾天图像进行处理，选取合适的阈值对图像的细节系数增强，经直方图匹配修正得到增强后的雾天图像。实验结果表明：该方法对雾气图片处理后，图像的细节和层次感得到了提高，视觉效果明显改善，是一种有效的雾天图像清晰化方法。

[关键词]波粒重构；均衡化；阈值

近年来，天气的反常变化越来越多，有些地方一年有一大半时间被雾笼罩。而在雾天获取图像，会受雾气的干扰，获得的照片比较模糊。所以，需要分析如何减弱噪声的影响，在雾天中获取到更加清晰的图像，具有重要的实际意义。

本文根据雾天中图像对比度不高的特点，采用了波粒分析的图像去噪[1]方法，先对相机获取的图像二值均衡化处理，然后对图像采用波粒变换，选取适当阈值，且对阈值作系数处理，再对修改后阈值波粒重构，得到重构后的图像再进行直方图匹配修正，最终获得雾天清晰化图像。

本文的图像去噪系统框图如图1所示。

图1　图像去噪系统框图

1直方图均衡化

对于普通获取的图像，设s和r分别表示变换后图像和被增强图像的灰度。先假定所有像素的灰度已归一化。即当r=s=0时，表示黑色；当r=s=1时，表示白色；变换函数T(r)与原图像概率密度函数p(r)之间的关系为

(1)

式中r为积分变量。

要让这种灰度变换有实际意义，则规定T必须满足如下条件：在0≤r≤1区间内，T(r)为单调增加。用p(r)表示原图像概率函数。在已知p(r)和变换函数s=T(r)时，反变换函数r=T-1(s)也是单调增加，则

(2)

将(1)式代入(2)式，则

(3)

由以上公式可见，概率密度在变量s的定义域内是均匀分布的。可以得到图像局部灰度动态显著增强，所以也提高了图像的对比度。离散化后的变换函数为

(4)

图2为原始图像，利用(4)式可以把灰度级为rk的像素映射成相应的灰度级为sk的像素，从而实现均衡化，结果如图3所示。

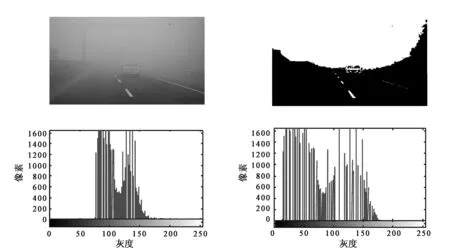
图2　原始图像　　　　　　　　　　　图3　均衡化后直方图

由于直方图均衡化后的图像的动态范围扩大，扩大的本质是量化层间隔扩大，而并非数目扩大。因此造成图像灰度级的减少，同时图像细节的灰度分布频数往往较少，如图3所示。所以直接处理均衡化后图像可能造成某些细节的丢失，甚至出现异常现象，使处理后的图像视觉效果无法达到要求。

2波粒理论

自然图像的结构相对比较复杂，含有丰富的噪声信息，所以有必要对噪声信息进行研究。波粒理论是阿贝尔等提出的一种基于多维度分析方法[3]。与普通小波相比，波粒提供稀疏的表示方法来表示噪声图像，可以抓捕到图像的噪声信息和奇异特征[4]。

定义波粒子函数φu(x)，下标u=(j,m,n)=(j,m1,n1,m2,n2)，j,m1,n1,m2,n2∈Z,相对空间的某一点(xu,wu)满足关系式：

(5)

其中C1,C2>0是常数。xu,wu分别是波粒子φu(x)在空域和频域的核心，粒子在相空间点(xu,wu)处需满足下面的不等式方程：

(6)

(7)

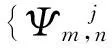
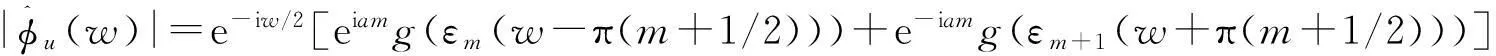
(8)

(9)

在任意u(x)∈L2(R)，2-j尺度上的空间频域波粒系数为

(10)

根据Plan关系，可得出中频域的波粒系数：

(11)

3波粒去噪

假定用f=u+η表示含有污染的图像,其中u为纯净图像,去噪原理是从f中还原出目标图像u,波粒去噪是为了滤除干扰视觉信息，从而得到目标信息。图像纹理和边沿是图像的重要组成部分，在对图像处理时不能不顾图像的边沿而使得图像变得模糊。由于硬阈值断续性和周期影响，波粒去噪时也在图像的断续点邻域产生伪Gibbs震荡[6]，出现了其它方向性集体失真。这种失真可以看成整体震荡，但是正则化可以抑制整体震荡。引入正则化抵消失真，故提出波粒系数去噪改进算法。

从图像的角度，去噪明显是一个局部不定性的逆向问题，故引入约束条件得到稳定解，约束条件可以通过正则化方程描述。若函数u(x)∈L1(Ω)，u(x)∈L1(Ω)，则u(x)的全差定义为

(12)

其离散近似表示为

(13)

其中ai,j=ui+1,j-ui,j,bi,j=ui,j+1-ui,j,ci,j=ui,j-ui+1,j,di,j=ui,j-ui,j+1。当噪声方差σ一定时，图像去噪的模型表示为

(14)

引入拉格朗日乘子λ，模型(14)可变为无约束条件的变分模型：

(15)

建立去噪后恢复模型：

(16)

公式中BV为有界函数，若令V={v:v∈BV(Ω),WAu(v)=0,u∈Λ}，则定义U为它的仿射空间，它的方向由V确定，模型(17)的目标函数明显是凸函数，故U空间函数也是凸的，使用梯度投影[7]迭代求解：

(17)

其中τk>0是迭代步长，pv表示在V空间正交投影，g(TV(uk))则表示是次梯度，即

(18)

(19)

图4　波粒重构后图像

综上所述，波粒子去噪算法首先对含有噪声图像f作波粒子变换WAu(f)=〈f,φu〉，对变换后系数求解非线性阈值，最后采用波粒重构uk+1，对得到的uk开始修正，取k=1，令迭代次数为K，确定步长估计值τk，结合公式(18)和(19)，输出最终去噪后的图像uk+1，图4为波粒重构后的图像，图像对比度明显增强。

雾对图像的主要影响是在频域中表现低频信息，故对雾天中的图像使用小波分解，分解层数越多，去雾效果越好，考虑到实际编程的难度和效果，选择分解4层。在小波的4层分解时，每层的小波系数都是根据低频系数分解而成。因此选用极小极大原理对阈值进行匹配，得到最小均方误差[8]。利用这个阈值对分解出的每层高频系数用软阈值处理。对处理后的系数进行小波重构，得到新的图像。

4图像直方图匹配修正

图像采用直方图均衡进行修正，可以灵活地产生变换函数[9]，以获取到的图像直方图为基准。一般是扩展原始图像的灰度级别来实现图像对比度的增强，但是这种方法的随机性很强。图5是在MATLAB中实现直方图修正匹配。

用直方图匹配修正法处理波粒重构图像，可以看出图像的视觉效果得到明显提高，对比度均衡扩散，图像整体增强。如图5所示,处理后的直方图趋于平缓；如图6所示，说明了波粒去噪后的图像噪声减少，对比度增强，图像清晰。

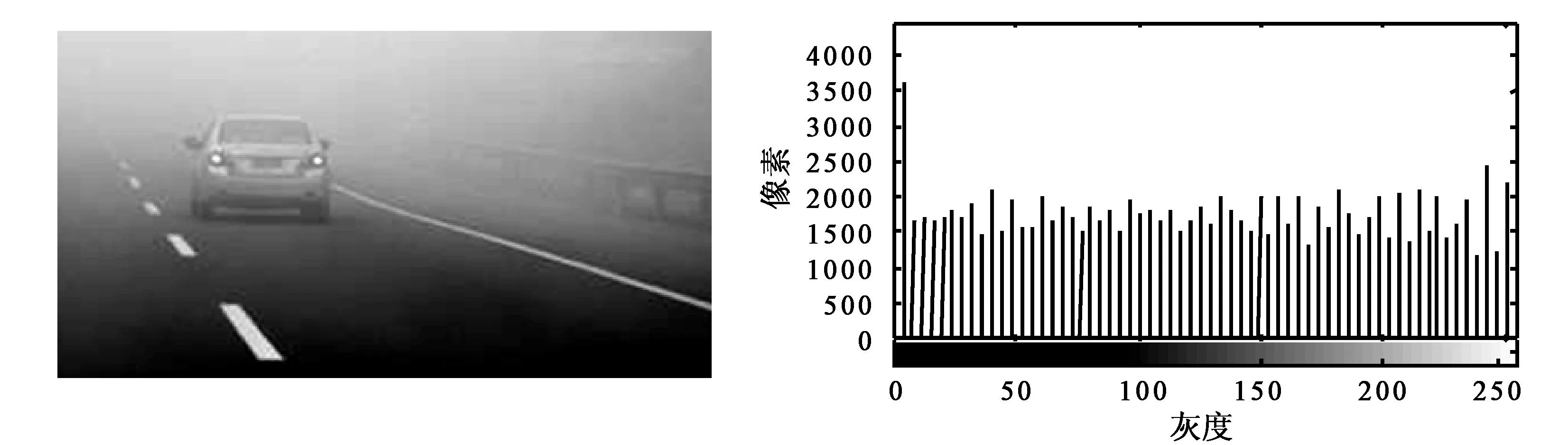
图5　直方图修正后图像　　　　　　　　　 图6　修正后直方图

对修正后的图像重构，可以得到各层低、高频系数；利用极大极小原理选取阈值，对分解出的高频系数阈值处理。使得直方图移向暗区，可以观察到图像的效果明显较好。

5实验结果及分析

为了验证算法的有效性，随机在雾天获取了1 000张图片测试,比较本文的算法与其它算法性能差别。为了对去噪方法性能进行比较，选用SRAD和PM算法与本文方法进行对比，SRAD算法步长为0.01，迭代次数大约为200。而PM算法对比度变量为30，参数是正常步长的0.3倍。而本文的波粒重构方法迭代次数仅为200。

为了更具有说服力，表1中对比了同一图像不同方法去噪的几个指标的结果：峰值信噪比PSNR, 均方差MSE，图片的质量指标Q。普通方法是将其对数变换转换为高斯噪声后进行处理，但是本文的方法是先将图像直方图二值均衡化后进行波粒重构，最后匹配修正，这样就可以直接对细节子带进行滤波，而不需要进行同态处理。

表1　不同的去噪方法实验结果对比

从实验结果可以看出本文方法的均方差MSE值大于SRAD算法，但其它两值均优于SRAD和PM[10]，本文方法起到了明显去噪效果，然而通过对比发现在均方差方面还存在不足，事实上，无论采取什么样的去噪途径对噪声的抑制改善，它们不太可能去除图像中的全部噪声。所以在不断改善去噪技术的同时应结合其它去噪方法的优点，在实际应用中将它们结合到一起。

6结论

通过仿真对比分析，本文建立的波粒重构模型经过直方图匹配修正，对雾天获取的含有噪声的图像有明显清晰化效果，与常规方法相比，不仅大大提高图片的信噪比，而且也提高了质量指标Q。在未来的交通、国防等领域具有一定的实用价值。

[参考文献]

[1]李彦,汪胜前,邓承志.多尺度几何分析的图像去噪方法综述[J].计算机工程与应用,2011(34):168-171.

[2]陈小晴.基于偏微分方程的图像去噪方法研究[D].南京：南京信息工程大学,2013.

[3]吕铁英，彭嘉雄.一种基于数学形态学的多尺度分析方法研究[J].数据采集与信号处理,1998,13(2):180-185.

[4]张宗常.特征交换框架下奇异特征的处理[J].计算机工程报,2011(1):81-86.

[5]郭彤颖,吴成东,曲道奎.小波变换理论应用进展[J].信息与控制学报,2004，33(1):67-69.

[6]JANMEY P A. Polymerization of fibrin: analysis of light-scattering data and relation to a peptide release[J].Biopolymers,1983,22(9):221-225.

[7]毕亚倩.求解界约束优化的一种新非单调谱投影梯度法[J].计算机数学,2013(4):205-207.

[8]张丹丹,张禾,刘慧芳.最小均方误差均衡器的Matlab仿真设计[J].现代电子技术,2010(19):54-56.

[9]胡春平,黄金锋,冯佰威.基于变换函数的船体曲面参数化修改技术研究[J].武汉理工大学学报：交通科学与工程版，2013，37(2):377-380.

[10]杨先凤,彭博.SRAD-高斯金字塔模型研究[J].计算机工程,2012(4):38-45.

[责任编辑：李 莉]

An image sharpening method based on wave-particle denoising

ZHAO Ming-min，TIAN Li，DU Dao-chang，BAO Wei，CHEN Yong

(School of Electric Engineering， Anhui Polytechnic University， Wuhu 241000， China)

Abstract:In order to cope with the disadvantage of lower image contrast and the poor visibility in foggy weather, this paper presents a method based on wave-particle reconstruction. After processing the foggy image in equalization method, we use the wave-particle reconstruction to process the graph, and then select the appropriate threshold for detail coefficient image enhancementand histogram matching amendment greatly enhanced the fog image. The results show that after processing the foggy image in this way, image detail and depth has been improved and visual effect improved significantly. The method proves to be effective in coping with the foggy image.

Key words:wave-particle reconstruction;equalization;threshold

作者简介：赵明敏(1988—)，男，江苏省盐城市人，安徽工程大学硕士研究生，主要研究方向为数字图像处理、模式识别；[通信作者]田丽(1962—)，女，安徽省芜湖市人，安徽工程大学教授，硕士生导师，主要研究方向为复杂系统建模与仿真。

基金项目：国家中小企业创新基金资助项目(11C26213402044)

收稿日期：2015-04-24

[中图分类号]TP391.41

[文献标识码]A

[文章编号]1673-2944(2015)06-0023-05