混凝土早龄期力学性能的影响因素

周勇，高杰，屈文俊

(同济大学 建筑工程系，上海 200092)



混凝土早龄期力学性能的影响因素

周勇，高杰，屈文俊

(同济大学 建筑工程系，上海 200092)

摘要:混凝土在龄期12 h~2 d表现出明显的塑性，为了避免受力后引起较大的侧向位移，采用一种无损检测方法——冲击共振法，可以快速准确地测出混凝土早龄期动态弹性模量，并通过它与静力受压弹性模量的线性关系推算出静力受压弹性模量。试验研究骨料体积含量、粗骨料级配、粗骨料种类、水灰比和养护温度对混凝土轴心抗压强度和弹性模量的影响，进一步分析在相同龄期时，哪些因素是重要因素。研究得出水灰比是轴心抗压强度的重要影响因素，骨料体积含量是弹性模量的重要影响因素。同时，采用多元回归分析建立上述影响因素与强度和弹性模量相关关系的数学表达式。

关键词：早龄期；冲击共振法；影响因素；重要性分析；多元回归分析

混凝土早龄期力学性能随龄期快速变化，对混凝土结构施工有着重要的影响，尤其是混凝土早龄期强度和弹性模量对施工过程起控制作用。对于高层结构，混凝土早龄期强度与弹性模量是控制拆模时间的重要指标。在强度和弹性模量不满足要求的情况下，过早拆模，结构难以承受自重或变形过大而出现裂缝甚至倒塌，将造成重大的质量事故。对于后张拉预应力结构，混凝土早龄期强度和弹性模量决定张拉时间。混凝土在龄期12 h~2 d内，水泥石强度较低，表现出明显的塑性。此时，采用传统静力加载方式测量混凝土的弹性模量极易引起较大的侧向位移从而影响测量精度。为了避免试验误差，采用一种无损检测方法——冲击共振法，测量混凝土早龄期动态弹性模量。通过建立动态弹性模量与静力受压弹性模量的关系，用容易精准测量的动态弹性模量推算出静力受压弹性模量。这种方法不仅大量节省了试验时间，方便快捷，准确有效，而且不损坏试件，有效利用试件。Stock等[1]研究得出轴心抗压强度在骨料含量0-0.4范围内，随着骨料体积含量的增加而减小，骨料含量大于0.4时，随着骨料体积含量的增加而增大；静力受压弹性模量随着骨料体积含量的增加而增大。Johnson等[2]研究得出混凝土抗压强度与动态弹性模量都随着骨料体积含量的增加而增大，随着水灰比的增大而减小，骨料体积含量和水灰比对抗压强度的影响大于对动态弹性模量的影响。黄政宇[3]指出混凝土抗压强度受水泥强度、水灰比、骨料表面状况、骨料最大粒径及养护温度的影响；静力受压弹性模量与骨料和水泥石的弹性模量及骨料的体积含量有关。周士琼[4]指出混凝土的强度主要决定于水泥石的强度和水泥石与骨料之间的黏结强度；混凝土的静力受压弹性模量通常随着抗压强度的增高而增大，影响弹性模量的因素基本上与影响混凝土强度的因素相同。静力受压弹性模量还与骨料和水泥的相对含量以及水泥石与骨料的弹性模量有关。Yldrm等[5]研究得出水灰比、最大骨料粒径和骨料种类对混凝土弹性模量有影响。Ranchero[6]指出混凝土强度的影响因素基本上与弹性模量的影响因素相同，主要受水灰比、粗骨料种类和骨料体积含量的影响。Kim等[7]研究得出静力受压弹性模量与动态弹性模量的关系不受养护温度的影响。上述文献主要研究了龄期28 d以及更长龄期，影响因素对混凝土轴心抗压强度和弹性模量的影响。缺少对早龄期轴心抗压强度和弹性模量的研究。本文不仅研究了龄期12 h~28 d，骨料体积含量、粗骨料级配、粗骨料种类、水灰比和养护温度对混凝土轴心抗压强度和弹性模量的影响，而且研究了在相同龄期时，哪些因素是重要因素，哪些是次要因素。同时，建立了影响因素与轴心抗压强度和弹性模量相关关系的数学表达式。

1试验设计

1.1　材料特性

试验的主要材料：P.O 42.5海螺牌水泥，卵石(最大粒径20 mm)，碎石(最大粒径16，20和31.5 mm)，中砂(河砂)。

对试验材料进行了材料特性试验，其中包括：粗骨料的筛分曲线、饱和面干密度、吸水率，细骨料的筛分曲线、饱和面干密度、吸水率。其中碎石5~31.5 mm的筛分曲线在孔径9.5 mm的累计筛余量为93%超出 《建设用卵石、碎石》[8](GB/T 14685—2011)规定的90%，其余骨料的筛分曲线都符合规范要求。

1.2　试验配合比设计

试验主要研究骨料体积含量、粗骨料级配、粗骨料种类、水灰比和养护温度对混凝土轴心抗压强度和弹性模量的影响，分别对这5种影响因素进行配合比设计。设计时水泥的密度取3 150 kg/m3，每m3混凝土含孔隙体积为0.01 m3，砂率均为33%，采用绝对体积法进行配合比设计，见表1。SJ1~SJ4研究骨料体积含量的影响，采用骨料体积0，0.4，0.65，0.75和相同的水灰比(0.5);粗骨料(碎石最大粒径16 mm)；SJ5~SJ7研究粗骨料级配的影响，分别采用碎石最大粒径16 mm，碎石最大粒径20 mm，碎石最大粒径31.5 mm和相同的水灰比(0.5)；骨料基体含量(0.65)；SJ8~SJ9研究粗骨料的影响，分别采用碎石最大粒径20 mm，卵石最大粒径20 mm和相同的水灰比(0.5)；骨料基体含量(0.65)；SJ10~SJ12研究水灰比的影响，分别采用水灰比0.35，0.5，0.6和相同的骨料体积含量(0.65)，碎石最大粒径16 mm；SJ13~SJ14研究养护温度的影响，分别在21±0.5℃和33.5±1℃养护，采用相同的配合比。

表1　混凝土配合比

1.3　试件制作和准备

试件选用边长为100 mm×100 mm×300 mm的棱柱体试件，每种配合比浇筑50个试件。浇筑时充分振捣，浇筑完成后用塑料薄膜包裹试件，防止水分蒸发。龄期12 h后拆模，将试件放到饱和Ca(OH)2溶液中恒温养护，以防止水泥水化产物Ca(OH)2的析出。养护温度为21±0.5 ℃和33.5±1 ℃。

2试验过程

2.1　轴心抗压强度和静力受压弹性模量

参照《普通混凝土力学性能试验方法标准》[9](GB/T 50081—2002)，每种配合比分别在龄期12 h,1,2,3,7,14和28 d进行试验，每次试验6个试件，3个测轴心抗压强度，3个测静力受压弹性模量，试件变形采用引伸计(标距长度100 mm，量程±6 mm)测量，按照规范要求对试验数据取值。

2.2　动态弹性模量

参照《Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens》[10](ASTM C 215-08)，选用纵向共振频率测量试件的动态弹性模量，在测量静力受压弹性模量试验前，测量试件的动态弹性模量，如图1。

混凝土动态弹性模量按下式计算：

图1　仪器安装位置Fig.1 Locations of impact and accelerometer

Ed=DMn2

(1)

D=4(L/bt)

(2)

式中：Ed为动态弹性模量；L为试件长度，m；b和t为试件截面尺寸，m；M为试件质量，kg；n为共振频率的平均值，Hz。

3试验结果分析

3.1　静力受压弹性模量与动态弹性模量的关系

Ranchero[6]研究得出对于相同配合比的混凝土，动态弹性模量与静力受压弹性模量成线性关系；动态弹性模量试验时，混凝土的应变较小，因此动态弹性模量大于静力受压弹性模量。Neville[11]研究得出在动态弹性模量试验中，试件是不受力的，没有蠕变的影响。因此动态弹性模量基本上与初始切线模量相同，比静力受压弹性模量大。根据英国规范CP110：1972，静力受压弹性模量与动态弹性模量的线性关系为

Ec=1.25Ed-19

(3)

式中：Ec代表静力受压弹性模量;Ed代表动态弹性模量，GPa。

Han等[12]研究得出静力受压弹性模量与动态弹性模量的关系为：

Ec=Ed(1-ae-bEd)

(4)

采用线性拟合与拟合公式(4)对SJ3的试验数据进行拟合，得到的结果见图2。

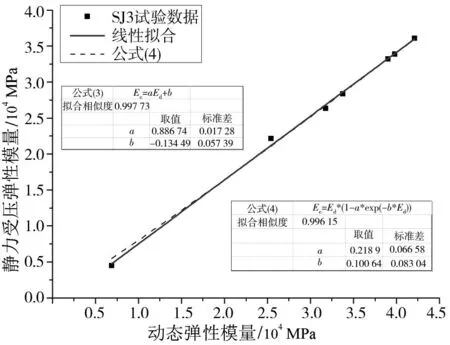
图2　SJ3静力受压弹性模量与动态弹性模量的关系Fig.2 Relationship between Ec and Ed of SJ3

通过对拟合图形的分析，可以得出线性拟合与Han研究得出的拟合公式(4)均与试验数据拟合较好，但线性关系简单，便于计算，而且拟合相似度更接近1。SJ1~SJ14试件均有相同的特征，因此建议采用线性关系表征混凝土静力受压弹性模量与动态弹性模量的关系。

3.2　骨料体积含量的影响

试验结果表明随着骨料体积含量的增加，混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量都增大，如图3所示。未出现Stock等[1]研究得到在骨料体积含量0~0.4范围内，混凝土轴心抗压随着骨料体积含量的增加而减小的现象。骨料体积含量对弹性模量的影响大于对轴心抗压强度的影响，这与Johnson等[2]研究的结果不同。

骨料体积占混凝土体积的0.7左右，骨料强度大于水泥石强度，骨料的弹性模量高于水泥石的弹性模量，因此骨料体积含量是影响混凝土轴心抗压强度和弹性模量的重要因素，特别对弹性模量影响显著。

3.3　粗骨料级配的影响

对试验数据分析，粗骨料级配对混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量影响较小，试验值相差不大，规律性不强，如图4所示。原因可能是各粗骨料的累计筛余和级配曲线相差不大，对混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量影响较小。此现象与Yldrm等[5]研究得出在相同的水灰比和骨料体积含量条件下，最大粒径为32，16和8 mm对混凝土弹性模量的影响相差较小的现象相同。但最大粒径为4 mm对混凝土弹性模量影响较大。因为最大粒径减小，骨料的表面积增加，界面区增多，导致混凝土弹性模量减小。

3.4　粗骨料种类的影响

在相同水灰比和骨料体积含量条件下，试验研究了最大粒径20 mm的碎石和最大粒径20 mm的卵石对混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量的影响，如图5所示。由于碎石表面粗糙，与水泥石的黏结力大，卵石表面光滑，黏结力较小，因此碎石混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量都大于卵石的。

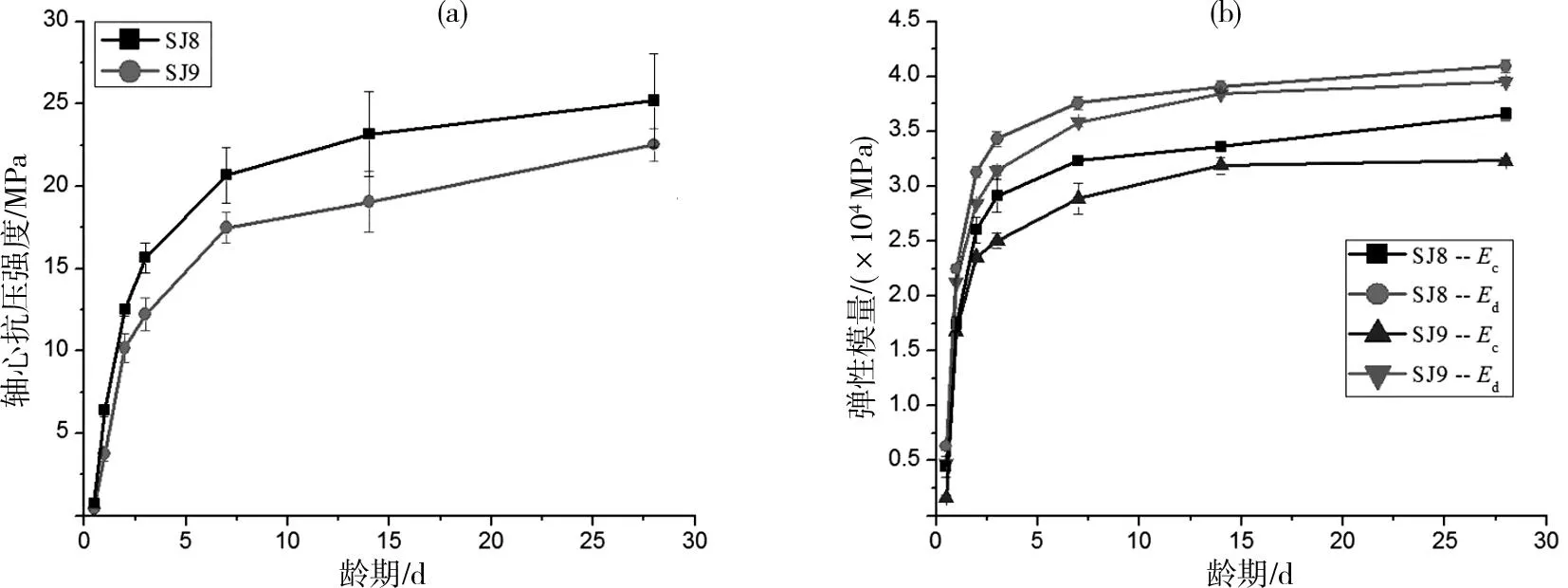
(a)轴心抗压强度；(b)弹性模量图5　粗骨料种类的影响Fig.5 Influence of type of coarse aggregate

(a)轴心抗压强度；(b)弹性模量图4　粗骨料级配的影响Fig.4 Influence of grade of aggregate

3.5　水灰比的影响

在相同骨料体积含量条件下，试验研究了水灰比为0.35，0.5和0.6对混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量的影响，如图6所示。

水灰比影响水泥石的强度，对混凝土强度和弹性模量有重要的影响。水灰比越小，水泥石的强度越大，水泥石与骨料的黏结力越大，因此混凝土的轴心抗压强度、静力受压弹性模量和动弹性模量也越大。通过对试验数据分析，可以得出随着水灰比的减小，混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量都增大。但是轴心抗压强度的增大幅度大于静力受压弹性模量和动态弹性模量的增大幅度，这与Johnson等[2]研究的结果相同。

(a)轴心抗压强度；(b)弹性模量图6　水灰比的影响Fig.6 Influence of water to cement ratio

3.6　养护温度的影响

在相同配合比条件下，试验研究了养护温度21±0.5 ℃、33.5±1 ℃对混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量的影响，见图7。随着养护温度的升高，混凝土轴心抗压强度、静力受压弹性模量和动态弹性模量都增大，但是轴心抗压强度的增大幅度大于静力受压弹性模量和动态弹性模量的增大幅度。因为混凝土弹性模量在龄期3d内迅速增长，养护3 d的弹性模量大约是养护28 d的80%，养护温度对弹性模量影响不明显。

(a)轴心抗压强度；(b)弹性模量图7　养护温度的影响Fig.7 Influence of curing temperature

3.7　影响因素重要性分析

采用多元回归分析研究同一龄期各因素对强度和弹性模量的影响，并且分析得出哪些因素是重要因素，哪些是次要因素。在多元回归分析时，粗骨料类型为虚拟数据而且粗骨料是卵石的试件远少于碎石的试件，为了分析的准确性，不考虑粗骨料类型的影响。

用EViews软件[13]进行多元回归分析，使用对数方程的回归效果优于线性方程，骨料体积含量存在取0值的情况，回归前加一个较小的数来提高精度，因此回归方程为：

log(fc/Ec/Ed)=a1log(x1+0.1)+a2log(x2)+

a3log(x3)+a4log(x4)+C

(5)

其中，fc，Ec和Ed分别代表混凝土轴心抗压强度，静力受压弹性模量，动态弹性模量；x1,x2,x3和x4分别代表骨料体积含量，粗骨料级配，水灰比和养护温度；a1,a2,a3和a4代表影响因素的系数；C为常数项。

多元回归分析结果见表2，当影响因素系数的概率大于0.1时，说明该影响因素对结果影响不显著。因此分析得出：对轴心抗压强度，在龄期12 h时，各因素的影响次序为养护温度>水灰比，骨料体积含量和粗骨料级配影响不显著；在龄期1~7 d时，影响次序变为水灰比>养护温度>骨料体积含量，粗骨料级配影响不显著；在龄期14~28 d时，影响次序为水灰比>养护温度>骨料体积含量>粗骨料体积含量。对于静力受压弹性模量和动态弹性模量，在龄期12 h时，各因素的影响次序为养护温度>骨料体积含量，粗骨料级配和水灰比影响不显著；在龄期1 d时，影响次序变为水灰比>骨料体积含量，粗骨料级配和养护温度影响不显著，在龄期2~28 d时，骨料体积含量影响显著，粗骨料级配、水灰比和养护温度影响不显著。

总结上述分析，轴心抗压强度在龄期12 h时受养护温度影响显著，龄期1~28 d受水灰比影响显著，其次是养护温度，骨料体积含量和粗骨料级配影响较小；弹性模量在12 h时，受养护温度影响显著，在龄期1 d时，受水灰比影响显著，在龄期2~28 d时，受骨料体积含量影响显著，粗骨料级配、水灰比和养护温度影响不显著。水灰比是轴心抗压强度的重要影响因素，骨料体积含量是弹性模量的重要影响因素。

3.8　相关关系的数学表达式

将骨料体积含量、粗骨料级配、水灰比、养护温度和龄期T作为强度和弹性模量的影响因素，应用多元回归分析确定这些因素与强度和弹性模量相关关系的数学表达式。在龄期12 h~2 d时，强度和弹性模量快速增长，弹性模量增长速率快于强度的增长速率，在龄期2 d后，增长速率减慢，所以表达式采用分段函数，分别对强度和弹性模量建立它们与影响因素的数学表达式，结果如下：

(6)

(7)

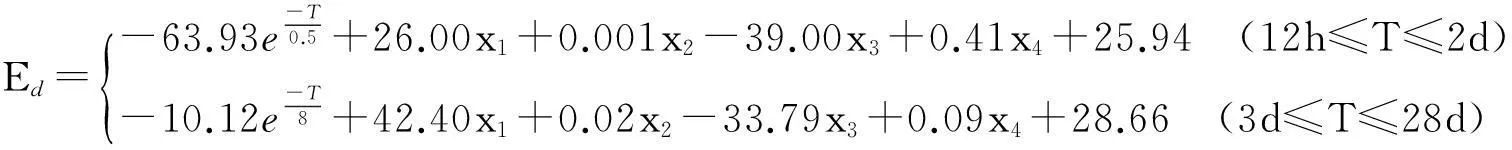
(8)

表2　各影响因素的回归系数

回归值与试验值的对比见图8，在龄期12 h~2 d时，多数回归值与试验值相差较少，只有少数回归值与试验值相差较大，回归的可决系数R2均高于0.911；在龄期3~28 d时，所有回归值与试验值相差极小，回归的可决系数R2均高于0.949，甚至高达0.987。因此说明多元回归分析有效。此外，通过对各影响因素系数的分析，可以得出水灰比对轴心抗压强度影响显著，骨料体积含量对弹性模量影响显著，粗骨料级配对强度和弹性模量影响不显著。

(a)龄期12 h~2 d，轴心抗压强度；(b)龄期3~28 d，轴心抗压强度；(c)龄期12 h~2 d，静态弹性模量；(d)龄期3~28 d，静态弹性模量；(e)龄期12 h~2 d，动态弹性模量；(f)龄期3~28 d，动态弹性模量；图8　回归值与试验值的对比Fig.8 Comparison the results of regression and the experimental data

4结论

1)混凝土静力受压弹性模量与动态弹性模量成线性关系。

2) 轴心抗压强度在龄期12 h时受养护温度影响显著，龄期1~28 d受水灰比影响显著，其次是养护温度，受骨料体积含量和粗骨料级配影响较小；弹性模量在12 h时，受养护温度影响显著，在龄期1 d时，受水灰比影响显著，在龄期2~28 d时，受骨料体积含量影响显著，粗骨料级配、水灰比和养护温度影响不显著。水灰比是轴心抗压强度的重要影响因素，骨料体积含量是弹性模量的重要影响因素。

3)采用多元回归分析，研究得出了影响因素与强度和弹性模量相关关系的数学表达式。回归的可决系数R2均高于0.911，多元回归分析准确有效。

参考文献：

[1] Stock A F, Hannantt D J, Williams R I T.The effect of aggregate concentration upon the strength and modulus of elasticity of concrete[J].Magazine of Concrete Research,1979,31(109): 225-234.

[2] Graft-Johnson J W S, Bawa N S.Effect of mix proportion, water-cement ratio, age and curing conditions on the dynamic modulus of elasticity of concrete[J].Building Science,1969,3(3): 171-177.

[3] 黄政宇.土木工程材料[M].北京：高等教育出版社, 2002.

HUANG Zhengyu.Civil engineering materials[M].Beijing: Higher Education Press,2002.

[4] 周士琼.土木工程材料[M].北京：中国铁道出版社, 2004.

ZHOU Shiqiong.Civil engineering materials[M].Beijing: China Railway Publishing House, 2004.

[6] Ranchero J L.Analyzing and determing relationships in elastic properties of concrete using wave propagation and vibration and uniaxial compression[D].Iuinois: University of Illinois at Urbana-Champaign, 2005.

[7] Kim J K, Han S H, Song Y C.Effect of temperature and aging on the mechanical properties of concrete: Part I.Experimental results[J].Cement and Concrete research, 2002, 32(7): 1087-1094.

[8] GB/T 14685—2011,建设用卵石,碎石[S].

GB/T 14685—2011,Pebble and crushed stone for construction[S].

[9] GB/T 50081—2002,普通混凝土力学性能试验方法标准 [S].

GB/T 50081—2002,Standard for test method of mechanical properties on ordinary concrete[S].

[10] ASTM C215-2008,Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens [S].

[11] Neville A M.Properties of concrete [M].4nd edition.Essex: Pitman Books Limited, 2011.

[12] Han S H, Kim J K.Effect of temperature and age on the relationship between dynamic and static elastic modulus of concrete[J].Cement and Concrete Research, 2004, 34(7): 1219-1227.

[13] 张晓峒.EViews使用指南与案例[M].北京：机械工业出版社, 2007.

ZHANG Xiaotong.A guide to using EViews[M].Beijing: China Machine Press,2007.

(编辑蒋学东)

Influential factors on mechanical property of concrete at early-age

ZHOU Yong , GAO Jie, QU Wenjun

(Department of Structural Engineering, Tongji University, Shanghai 200092, China)

Abstract:The concrete at the age of 12 h~2 d presents obvious plasticity.In order to avoid large lateral deformation, a nondestructive method—impact resonance method was applied, which can give the dynamic modulus of concrete at early age directly.The relationship between the modulus of elasticity of concrete and the dynamic modulus of concrete is linear.Therefore the modulus of elasticity of concrete can be calculated from the dynamic modulus of concrete.Meanwhile, the influences of the volume contents of aggregate, the grade and type of coarse aggregate, the water-cement ratio and the curing temperature on the prismatic compressive strength and the modulus of elasticity of concrete at early age were investigated.Furthermore, the importance of each influential factors were researched at the same age.It is proved that the water-cement ratio is the most important on the prismatic compressive strength and the volume content of aggregate is the most important on modulus of elasticity of concrete.The relationship between the influential factors and the prismatic compressive strength or modulus of elasticity of concrete is established by multivariate regression analysis.

Key words：early age; impact resonance method; influential factors; importance analysis; multivariate regression analysis

通讯作者：屈文俊(1958-)，男，河南辉县人，教授，博士，从事钢筋混凝土结构设计和耐久性的教学与研究；E-mail: quwenjun.tj@tongji.edu.cn

基金项目：国家自然科学基金青年科学基金资助项目(51208373)；上海市自然科学基金资助项目(14ZR1443300)

收稿日期：2015-03-25

中图分类号：TU502.6

文献标志码：A

文章编号：1672-7029(2015)06-1323-08