系杆拱桥拱肋内混凝土非对称浇筑量化影响分析
2016-01-25杜迎东王起才张戎令杨阳
杜迎东,王起才,张戎令,杨阳
(兰州交通大学 土木工程学院, 甘肃 兰州 730070)
系杆拱桥拱肋内混凝土非对称浇筑量化影响分析
杜迎东,王起才,张戎令,杨阳
(兰州交通大学 土木工程学院, 甘肃 兰州 730070)
摘要:为找到拱肋内混凝土非对称浇筑施工与对称浇筑施工的量化差异,使用三维有限元分析软件MIDAS/civil模拟拱肋对称浇筑和非对称浇筑2种情形,分别分析2种情形中拱肋和系梁在单侧浇筑一半(单侧筑半)、单侧浇筑完毕(单侧筑毕)、徐变3种工况下相同位置处的位移、弯矩变化规律,量化指出非对称浇筑的弊端。结果表明:非对称浇筑时拱肋的位移最大比对称浇筑的大26.1%,弯矩最大比对称浇筑的大164.3%;非对称浇筑时系梁的位移最大比对称浇筑的大24.3%,弯矩最大比对称浇筑的大13.4%,不宜非对称浇筑拱肋内混凝土。
关键词:系杆拱桥;非对称浇筑;量化影响

因结构自身具有经济美观、施工简便等优点,近年来,钢管混凝土拱桥在国内的修建方兴未艾。它以钢管混凝土特有的力学性能和技术优势,展示出强劲的生命力,在短时间内得到迅猛发展[1-3]。特别是在城区和城郊跨越公路、河流时其既可一跨跨越,又可起到景观的作用[4]。但是在实际工程中,由于施工场地、施工组织不合理等原因,非对称浇筑钢管内混凝土的现象时有发生,竣工后的桥梁既不能发挥其特有的力学性能又严重威胁施工安全。已竣工的一些大跨度拱桥,施工中不乏惊险情况和潜在危险,这其中就包含非对称施工造成的某些部位位移、内力偏大、失稳等情况。在施工过程对结构的应力、线形进行有效地监测和控制,以确保施工过程中每个构件的应力和变形均在允许的误差范围内[5-6]。许多学者对为了找到非对称浇筑对施工影响规律,进行了大量的研究。陈宝春[7]系统地阐释了钢管混凝土基本计算理论;郑建荣等[8]探讨了非对称浇筑施工对钢管混凝土拱肋稳定性的影响。基于有限元分析软件模拟不同施工工序,将非对称施工与对称施工结果对比,重点分析拱肋和系梁位移和内力变化规律,量化指出非对称施工的不合理性及不宜操作性,为后续同类型桥梁的建造提供参考,为继续优化施工组织、保证建造安全提供保证。
1研究背景
某系杆拱桥形式为钢管混凝土系杆拱,拱轴线为二次抛物线,矢跨比f/L=1/5,矢高26.5m,理论计算跨径128m,结构设计为刚性系梁刚性拱。系梁全长131m,采用满堂支架法施工,分5段浇筑,系梁采用全预应力混凝土单箱三室箱梁,梁高3.0m,梁顶宽14.7m,底宽12.04m。横桥向设置2道拱肋,拱肋中心间距11.4m,拱肋采用外径φ=130cm,壁厚δ=26mm的钢管混凝土哑铃形截面,拱肋内浇筑C55微膨胀混凝土,上下弦管中心距2.2m,拱肋截面高3.5m。全桥拱17组吊杆,每组吊杆分为左、右拱肋各1对,每对分为a和b2根吊杆,共68根吊杆。

2拱桥空间结构的有限元法
2.1 模拟方法
利用MIDAS/civil有限元分析软件以纵桥向为x轴,横桥向为y轴,竖向为z轴建立全桥三维有限元模型[9-10]。模型共495个节点,分为447个单元,系梁、拱肋、横撑均采用梁单元模拟,共379个梁单元,吊杆采用只受拉桁架单元模拟,共68个桁架单元。对称浇筑模型有9个施工阶段联合截面,非对称浇筑模型拱肋有18个施工阶段联合截面。建模时将钢材截面用等效的混凝土截面代替。系梁设置2个临时支座和4个永久支座。2个临时支座从系梁浇筑阶段一直持续到张拉完最后一根吊杆,4个永久支座在系梁支架拆除时全部激活。
吊杆采用体外力的方式张拉。主拱肋钢骨架重量按均匀分配的原则作用于相应结点上,横向联系与主拱圈刚性连接,吊杆和拱肋与主梁的连接根据吊杆锚固设计图先建立实际锚固点,然后与相应的拱肋和系梁梁节点间用刚性连接添加刚臂的方法模拟。混凝土弹性模量取为35.5 GPa,泊松比0.2,容重25 kN/m3,拱肋钢材弹性模量取为206 GPa,泊松比0.3,容重76.98 kN/m3,吊杆弹性模量取为205 GPa,泊松比0.3,容重78.5 kN/m3。
2.2 浇筑施工的有限元模拟
模型分别包含自重、预应力荷载、吊杆索力、二期荷载4种静力荷载工况,对称浇筑模型包括29个施工阶段。非对称浇筑模型先模拟浇筑负y轴侧,包括38个施工阶段。非对称浇筑时后浇筑的钢管与先浇筑的钢管考虑2d龄期差,对称浇筑与非对称浇筑正y轴侧混凝土龄期相同。分别对比对称浇筑和非对称浇筑下右拱肋在单侧筑半、单侧筑毕、徐变3种荷载工况下;系梁在单侧筑毕、徐变2种荷载工况下的位移和内力值,找出非对称浇筑与对称浇筑的量化差异。系杆拱桥全桥整体模型如图1所示。

图1 系杆拱桥全桥整体模型Fig.1 Whole model of the tied arch bridge
3有限元模型计算结果分析
由于左、右拱肋完全对称,这里仅以右拱肋为例进行分析。
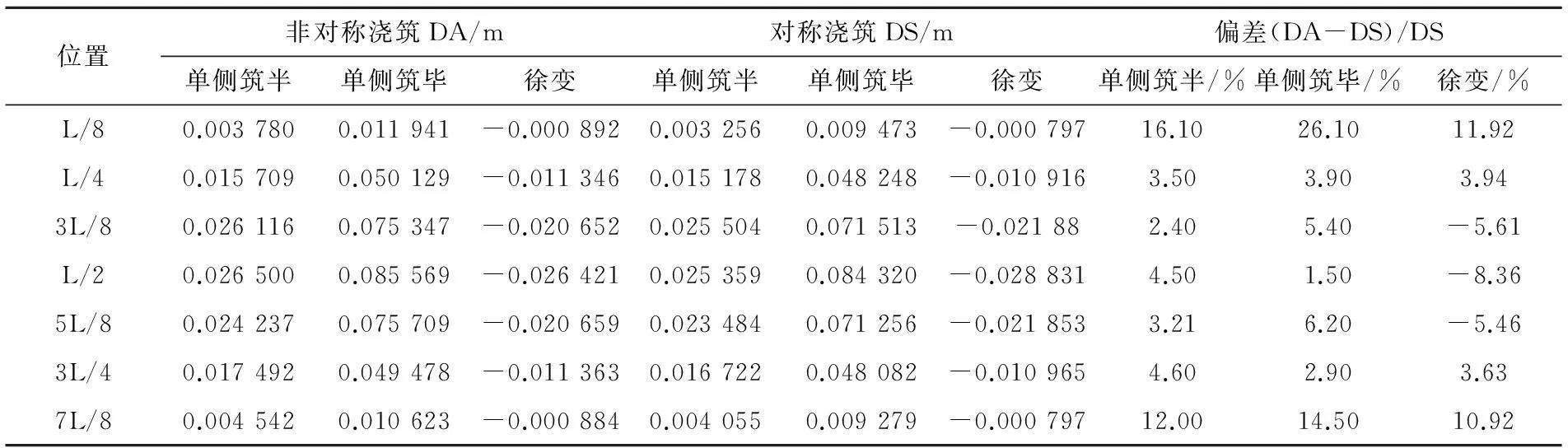
表1 2种浇筑方式右拱肋位移大小对比

表2 2种浇筑方式右拱肋弯矩大小对比

图2 2种浇筑方式右拱肋单侧筑毕下的位移对比Fig.2 Displacement comparison of the right side arch rib of two pouring ways in the condition of unilateral pouring over

图3 2种浇筑方式右拱肋徐变下的位移对比Fig.3 Displacement comparison of the right side arch rib of two pouring ways in the condition of creep

图4 2种浇筑方式右拱肋单侧筑毕下的相同截面弯矩对比

图5 2种浇筑方式右拱肋徐变下的相同截面弯矩对比Fig.5 Comparison of bending value on the same section of the right side arch rib of two pouring ways in the condition of creep
表1和表2中的单侧筑半工况与单侧筑毕工况2种浇筑方式的偏差变化规律大致相同,说明在混凝土浇筑施工中大量偏载作用下,拱肋位移、内力相比对称浇筑不利。从表1和图2、图3可以看出,单侧筑毕工况下,非对称浇筑时右拱肋各个位置的位移值相比对称浇筑时大。右拱肋在单侧筑毕工况下:L/4,3L/8,L/2,5L/8和3L/4位置处非对称浇筑与对称浇筑竖向位移相差不大,L/8和7L/8位置处2种浇筑方式竖向位移偏差较大,超过了工程上要求的5%左右的偏差限值,分别为26.2%和14.5%;在徐变工况下非对称浇筑主要影响距离拱肋和系梁连接处较近的L/8和7L/8等位置,这主要是由于该处截面、材料突变,钢拱圈内力要逐渐传给拱脚结点的混凝土,钢拱肋与拱脚结点相交处出现了应力集中现象,影响了距其较近的右拱肋L/8和7L/8等位置。图1和图2可以看出:单侧筑半、单侧筑毕工况下位移值均为正值,徐变工况位移值均为负值,说明徐变对竖直向下的挠度产生抵消效应。
从表2和图4、图5可以看出,单侧筑毕工况下,非对称浇筑时比对称浇筑时相同截面弯矩值要大。右拱肋在单侧筑毕工况下:3L/8,L/2和5L/8位置处非对称浇筑与对称浇筑弯矩值偏差不大,L/8,L/4,3L/4和7L/8位置处2种浇筑方式弯矩值的偏差较大,分别为163.3%,70.5%,64.3%和164.3%;在徐变工况下2种浇筑方式右拱肋除3L/8,L/2,5L/8和3L/4位置弯矩偏差稍大外,其他部分偏差均在5%左右,在可接受范围内。L/8,L/4,3L/4和7L/8处弯矩值为负,说明拱腹受压,拱背受拉。在3L/8,L/2和5L/8位置处,非对称浇筑在徐变工况下的弯矩值小于对称浇筑的弯矩值,这是由于这3个位置处所安装的吊杆属于长吊杆,其索力采用考虑转动惯量和剪切变形耦合的铰接吊杆索力实用计算公式[10]可以计算得较为精确,较精确的吊杆索力可以对非对称浇筑产生有利影响。
从表3和图6、图7可以看出,单侧筑毕工况下,非对称浇筑时系梁各个位置的位移相比对称浇筑时大。系梁在单侧筑毕工况下:L/8和7L/8位置处非对称浇筑与对称浇筑竖向位移值偏差不大,L/4,3L/8,L/2,5L/8和3L/4位置处2种浇筑方式的竖向位移值偏差较大,分别为21.40%,13.70%,20.70%,24.30%和21.80%;在徐变工况下仍是系梁L/8和7L/8位置处与对称浇筑位移值偏差较大,在徐变工况下的位移值均为负值。

表3 2种浇筑方式系梁位移大小对比

表4 2种浇筑方式系梁弯矩大小对比

图6 2种浇筑方式系梁单侧筑毕下的位移对比

图7 2种浇筑方式系梁徐变下的位移对比

图8 2种浇筑方式系梁单侧筑毕下的相同截面弯矩对比

图9 2种浇筑方式系梁徐变下的相同截面弯矩对比
从表4和图8、图9可以看出,单侧筑毕工况下,非对称浇筑时系梁大部分位置的弯矩值比对称浇筑时大。系梁在单侧筑毕工况下:L/8和7L/8位置处非对称浇筑与对称浇筑弯矩值偏差不大,其他位置如L/4,3L/8,L/2,5L/8和3L/4处与对称浇筑浇筑方式弯矩值的偏差较大,分别为39.88%,18.67%,31.03%,13.44%和38.29%;在徐变工况下2种方式系梁整体偏差稍不大,都在5%左右。
为了找到2种浇筑方式吊杆张拉后的差异变化,提取了68根吊杆全部张拉结束后2种浇筑方式右拱肋和系梁相同位置处位移和弯矩计算结果,如表5和表6所示。
从表5和表6可以看出,在吊杆张拉结束后,2种浇筑方式靠近两侧拱脚处的位移和弯矩值偏差较大。这主要是由徐变作用引起,虽然2种浇筑方式只考虑龄期相差2 d,起初徐变作用差异不大,但在混凝土达到等强度后,即进行吊杆张拉,结构内部转化为高次超静定结构,由于非对称浇筑的钢管核心混凝土龄期不同步,会出现次内力分布不同步,因而在位移和内力分布方面造成较大差异。此外,吊杆张拉结束后2种浇筑方式的偏差相比张拉之前的偏差整体偏小,这说明张拉吊杆对非对称浇筑的弊端可以产生抵消效应。

表5 全部吊杆张拉结束时两种浇筑方式右拱肋位移和弯矩对比

表6 全部吊杆张拉结束时两种浇筑方式系梁位移和弯矩对比
为了验证有限元模型的正确性,测试了实桥全部吊杆张拉结束后系梁各主要位置的位移、应力值并与模拟值进行比较,考虑到系梁单箱三室截面I=51.494 6 m4,由此换算出系梁各位置处截面上缘应力如表7所示。

表7 全部吊杆张拉结束后系梁有限元模拟与实测值比较
从表7可以看出,非对称浇筑有限元模拟的各个位置处截面上缘应力值与现场实测值基本吻合,偏差均在±5%以内,说明了有限元模型的正确性。
4结论
1)非对称浇筑拱肋的位移与对称浇筑的位移相比,最大偏差为26.1%,弯矩与对称浇筑相比,最大偏差为164.3%;非对称浇筑系梁的位移与对称浇筑位移相比,最大偏差为24.3%,弯矩与对称浇筑相比,最大偏差为13.4%。
2)在全部吊杆张拉结束后,2种浇筑方式位移和弯矩值受徐变作用影响,偏差稍大,但比单侧筑半、单侧筑毕工况时小。而张拉吊杆可对非对称浇筑的不利影响产生抵消效应。
3)非对称浇筑主要影响结构物建造过程中的位移和内力安全,为了保证结构建造过程中和运营过程中的线形要求及内力安全,系梁浇筑结束架设钢管后浇筑混凝土时不应进行非对称施工。
参考文献:
[1] 李乔,田学民,张清华.铁路大跨度提篮式系杆拱桥全桥模型试验[J].中国铁道科学,2003,24(1):88-93.
LI Qiao, TIAN Xuemin, ZHANG Qinghua.A model test on long-span X-style tied arch bridge on railway[J].China Railway Science, 2003,24(1):88-93.
[2] 陈强,向华伟,彭学理,等.大跨度钢桁拱桥架设过程控制技术[J].公路交通科技,2014,31(5):78-85.
CHEN Qiang, XIANG Huawei, PENG Xueli, et al.Erection progress control technique of long-span steel truss arch bridge[J].Journal of High and Transportation Research and Development,2014,31(5):78-85.
[3] 张起森,李雪莲,查旭东.黄河二桥系杆拱桥桥面铺装结构力学性能研究[J].土木工程学报,2006,39(7):88-93.
ZHANG Qisen, LI Xuelian, ZHA Xudong.Research on structure mechanics performance of the second yellow river bridge arc bridge deck pavement[J].China Civil Engineering Journal, 2006,39(7):88-93.
[4] 张戎令,王起才,马丽娜,等.考虑转动惯量和剪切变形耦合的铰接吊杆索力实用计算公式[J].中国铁道科学,2014,35(5):30-37.
ZHANG Rongling, WANG Qicai, MA Lina, et al.Practical figure for cable force of hinged suspender considering the coupling effect of moment of inertia and shear deformation[J].China Railway Science, 2014,35(5):30-37.
[5] 尚晋.中承式系杆拱桥施工控制研究[D].大连:大连理工大学,2013:1-84.
SHANG Jin.Study on construction control of half-through tied arch bridge[D].Dalian: Dalian University of Technology,2013:1-84.
[6] 刘军.系杆拱桥力学特性与稳定性分析[D].大连:大连理工大学,2009:1-62.
LIU Jun.Mechanical properties and stability analysis of tied arch bridge[D].Dalian: Dalian University of Technology,2009:1-62.
[7] 陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,1999.
CHEN Baochun.Design and construction of CFST arch bridge[M].Beijing:China Communication Press, 1999.
[8] 郑建荣,黄圣瑞,王淑妹,等.钢管混凝土拱桥拱肋混凝土灌注施工稳定研究[J].昆明理工大学学报(理工版),2009,34(6):62-65.
ZHENG Jianrong, HUANG Shengrui, WANG Shumei, et al.Stability research of concrete-filled-steel tube arch[J].Journal of Kunming University of Science and Technology(Science and Technology),2009,34(6):62-65.
[9] 王福春,梁力,李艳凤.下承式系杆拱桥拱脚局部应力有限元分析[J].沈阳建筑大学学报(自然科学版),2011,27(2):281-285.
WANG Fuchun, LIANG Li, LI Yanfeng.Finite element analysis of local stress at arch spring of through-type tied arch bridge[J].Journal of Shenyang Jianzhu University (Natural Science),2011,27(2):281-285.
[10] 北京迈达斯技术有限公司.MIDAS用户技术手册[M].北京:北京迈达斯技术有限公司,2004.
MIDAS IT(Beijing) Corporation.MIDAS/CW analysis for civil structures[M].Beijing:MIDAS IT(Beijing) Corporation,2004.
(编辑阳丽霞)
Quantitative analysis on asymmetrical pouring ofconcrete in the arch rib of tied arch bridge
DU Yingdong,WANG Qicai,ZHANG Rongling,YANG Yang
(School of Civil Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
Abstract:In order to explore the difference between asymmetrical and symmetrical construction,the large 3D finite element analysis software MIDAS/civil has been used to simulate two circumstances of arch rib symmetrical and asymmetrical pouring, The displacement and bending value variation law of the arch rib and tie beam of two circumstances respectively in the three conditions:unilateral pouring half,unilateral pouring over and creep are also analysed, Thus the disachvantages of asymmetrical pouring is pointed out.Results show that displacement of archlib and bending in asymmetrical pouring are 26.1% and 164.3% bigge than that in symmetrical pouring.Beside, tie beam displacement and bending in asymmetrical pouring are 24.3% and 13.4% bigger than that in symmetrical pouring.Thus asymmetric pouring concrete in arch rib is unreasonable.
Key words:tied arch bridge; asymmetric pouring; quantitative influence
通讯作者:王起才(1962-),男,河北晋州人,教授,博士,从事工程新材料预应力混凝土技术建筑及桥梁新结构的研究和开发;E-mail:13909486262@139.com
基金项目:长江学者和创新团队发展计划项目(IRT1139); 铁道部科技研究开发计划项目(2012G011-A)
收稿日期:2015-04-13
中图分类号:U448.22
文献标志码:A
文章编号:1672-7029(2015)06-1394-07
