严格α-预不变凸函数的若干性质

王海英，符祖峰

(安顺学院数理学院,贵州 安顺 561000)



严格α-预不变凸函数的若干性质

王海英，符祖峰

(安顺学院数理学院,贵州 安顺 561000)

摘要：首先，在中间严格α-预不变凸函数条件下，利用α-预不变凸性、半严格α-预不变凸性、上半连续性和下半连续性，得到了严格α-预不变凸函数的一些特征性质。其次，通过弱化γ∈(0,1)的一致性条件，在相对更弱的条件下，也获得了同样的结论。

关键词：严格α-预不变凸函数；α-预不变凸函数；半严格α-预不变凸函数；半连续函数

0引言

凸性及广义凸性是数学规划研究领域中的一项重要的研究内容，在最优化理论的研究中起到了重要作用。作为对凸函数的推广，人们先后提出了一些广义凸函数，例如预不变凸函数[1]、严格预不变凸函数[2]、半严格预不变凸函数[3]、α-预不变凸函数[4]、严格α-预不变凸函数[5]、半严格α-预不变凸函数[6]等，并且研究了这些广义凸函数的一些性质及在优化问题中的一些应用[7-11]。

本文注意到，在一定条件下，凸性可以通过中间点的凸性得到，预不变凸性也可以通过中间点的预不变凸性得到，而预不变凸函数是α-预不变凸函数的一种特殊情形。所以，本文在α-预不变凸、半严格α-预不变凸、上半连续和下半连续条件下，分别建立了严格α-预不变凸函数的一些类似结论。并且，在通过弱化γ∈(0,1)的一致性条件下，利用弱中间严格α-预不变凸性，也获得了同样的结论。

1预备知识

假设H是实Hilbert空间，K⊂H且K≠φ。α:K×K→R是实值函数，η:K×K→H是向量值函数。

定义1[4]如果对于∀x,y∈K，∀λ∈[0,1]，有y+λα(x,y)η(x,y)∈K，则称K是关于η和α的α-不变凸集。

定义2[4]设K是α-不变凸集，f是定义在K上的函数，如果对于∀x,y∈K，∀λ∈[0,1]，有f(y+λα(x,y)η(x,y))≤(1-λ)f(y)+λf(x)，则称f是K上的α-预不变凸函数。

定义3[5]设K是α-不变凸集，f是定义在K上的函数，如果对于∀x,y∈K，x≠y，∀λ∈(0,1)，有f(y+λα(x,y)η(x,y))<(1-λ)f(y)+λf(x)，则称f是K上的严格α-预不变凸函数。

定义4[6]设K是α-不变凸集，f是定义在K上的函数，如果对于∀x,y∈K，f(x)≠f(y)，∀λ∈(0,1)，有f(y+λα(x,y)η(x,y))<(1-λ)f(y)+λf(x)，则称f是K上的半严格α-预不变凸函数。

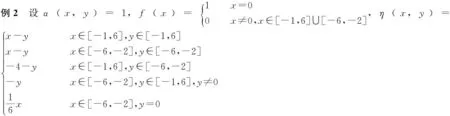
下面的条件和引理将在讨论严格α-预不变凸函数的一些性质时用到。

条件A[4]f(y+α(x,y)η(x,y))≤f(x)，∀x,y∈K；

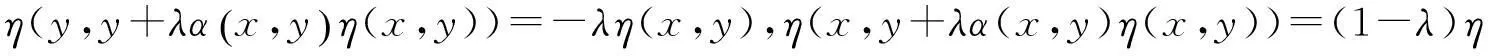
引理[7]∀x,y∈K，∀λ∈[0,1]，如果η和α满足关系式η(y,y+λα(x,y)η(x,y))=-λη(x,y)，α(x,y)=α(y,y+λα(x,y)η(x,y))，则∀γ1,γ2∈[0,1]，有α(y+γ1α(x,y)η(x,y),y+γ2α(x,y)η(x,y))=α(x,y)；η(y+γ1α(x,y)η(x,y),y+γ2α(x,y)η(x,y))=(γ1-γ2)η(x,y)。

2主要结果

本节假设：

1)K是关于η:K×K→H和α:K×K→R的α-不变凸集；

2)η满足条件C，α满足条件α(x,y)=α(y,y+λα(x,y)η(x,y))，f是K上的实值函数。

下面通过构建适当条件，在中间点的严格α-预不变凸性下，建立严格α-预不变凸函数的几个等价条件。

定理1f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f是K上的α-预不变凸函数；

2)条件Ⅱ：如果∃γ∈(0,1)，使得对∀x,y∈K，x≠y，均有f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)。

证明由严格α-预不变凸函数的定义可以直接得到必要性，只需证明充分性。

假设f不是K上的严格α-预不变凸函数，则至少存在两个点x,y∈K，x≠y，及某个λ∈(0,1)，有：

f(y+λα(x,y)η(x,y))≥λf(x)+(1-λ)f(y)

(1)

选取β1,β2且0<β1<β2<1，λ=γβ1+(1-γ)β2。令x*=y+β1α(x,y)η(x,y)，y*=y+β2α(x,y)η(x,y)，由题设条件Ⅰ，有：

f(x*)≤β1f(x)+(1-β1)f(y)，f(y*)≤β2f(x)+(1-β2)f(y)

(2)

同时由引理1可得y*+γα(x*,y*)η(x*,y*)=y+λα(x,y)η(x,y)，从而由题设条件Ⅱ，有：

f(y+λα(x,y)η(x,y))=f(y*+γα(x*,y*)η(x*,y*))<(1-γ)f(y*)+γf(x*)

(3)

根据式(2)、式(3)可得f(y+λα(x,y)η(x,y))<(1-γ)f(y*)+γf(x*)≤γ[β1f(x)+(1-β1)f(y)]+(1-γ)[β2f(x)+(1-β2)f(y)]=λf(x)+(1-λ)f(y)，这与式(1)矛盾，即证得f是在K上的严格α-预不变凸函数。

定理2f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f是K上的半严格α-预不变凸函数；

2)条件Ⅱ：如果∃γ∈(0,1)，使得对∀x,y∈K，x≠y均有f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)。

证明直接由严格α-预不变凸函数的定义可以得到必要性，只需要证明充分性。

设∀x,y∈K，x≠y，λ∈(0,1)，如果f(x)≠f(y)，由题设条件Ⅰ，有f(y+λα(x,y)η(x,y))<(1-λ)f(y)+λf(x)。如果f(x)=f(y)，由题设条件Ⅱ有f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)=f(x)=f(y)。记x*=y+γα(x,y)η(x,y)，下面分两种情况讨论：

x*+uα(y,x*)η(y,x*)=y+λα(x,y)η(x,y)

(4)

于是由题设条件Ⅰ和式(4)，可得f(x*+μα(y,x*)η(y,x*))<(1-λ)f(y)+λf(x)=f(x)。

综上，证得f是K上的严格α-预不变凸函数。

事实上，定理1的条件可以削弱，得到如下的结论。

定理3f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f是K上的α-预不变凸函数；

2)条件Ⅱ：如果对∀x,y∈K，x≠y，都∃γ∈(0,1)使得f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)。

证明由严格α-预不变凸函数的定义可以直接得到定理的必要性，只需证明定理的充分性。

对于∀x,y∈K，x≠y，∀λ∈[0,1],由题设条件Ⅱ，∃γ∈(0,1)，使得：

f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)

(5)

记x*=y+γα(x,y)η(x,y)，下面分两种情况考虑：

f(y+λα(x,y)η(x,y))<λf(x)+(1-λ)f(y)

(6)

2)当γ<λ<1时，同理可证得式(6)成立。

综上，证得f是K上的严格α-预不变凸函数。

同理，定理2的条件也可以削弱，得到如下的结论。

定理4f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f是K上的半严格α-预不变凸函数；

2)条件Ⅱ：如果对∀x,y∈K，f(x)≠f(y)，都∃γ∈(0,1)使得f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)。

下面，给出严格α-预不变凸函数与上半连续函数、下半连续函数之间的重要关系。

定理5f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f上半连续且满足条件A；

2)条件Ⅱ：如果∃γ∈(0,1)，使得对∀x,y∈K，x≠y均有f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)。

证明由严格α-预不变凸函数的定义可以直接得到定理的必要性，只需证明充分性。

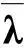
f(y+λ1α(x,y)η(x,y))-λ1f(x)-(1-λ1)f(y)=0

(7)

f(y+λ2α(x,y)η(x,y))-λ2f(x)-(1-λ2)f(y)=0

(8)

令x*=y+λ1α(x,y)η(x,y)，y*=y+λ2α(x,y)η(x,y)，则对∀β∈(0,1)，由于λ1<βλ1+(1-β)λ2<λ2，注意到λ1,λ2的取法,及引理1、(7)、(8)知，f(y*+βα(x*,y*)η(x*,y*))=f[y+λ2α(x,y)η(x,y)+βα(y+λ1α(x,y)η(x,y),y+λ2α(x,y)η(x,y))η(y+λ1α(x,y)η(x,y),y+λ2α(x,y)η(x,y))]=f[y+λ2α(x,y)η(x,y)+β(λ1-λ2)α(x,y)η(x,y)]=f[y+(βλ1+(1-β)λ2)α(x,y)η(x,y)]≥(βλ1+(1-β)λ2)f(x)+[1-(βλ1+(1-β)λ2)]f(y)=β[λ1f(x)+(1-λ1)f(y)]+(1-β)[λ2f(x)+(1-λ2)f(y)]=βf(y+λ1α(x,y)η(x,y))+(1-β)f(y+λ2α(x,y)η(x,y))=βf(x*)+(1-β)f(y*)，这与题设条件Ⅱ相矛盾，即f是K上的严格α-预不变凸函数。

定理6f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f下半连续且满足条件A；

2)条件Ⅱ：如果∃λ∈(0,1)，使得对∀x,y∈K，x≠y均有f(y+λα(x,y)η(x,y))<(1-λ)f(y)+λf(x)。

证明必要性可直接由严格α-预不变凸函数的定义得到，只需证明充分性。令A={λ∈[0,1]:f(y+λα(x,y)η(x,y))<λf(x)+(1-λ)f(y),∀x,y∈K,x≠y}。则由题设条件知，f在A上有定义。

因为f下半连续，所以f(y+λα(x,y)η(x,y))≤λf(x)+(1-λ)f(y)，即f是K上的α-预不变凸函数。根据定理1，f是K上的严格α-预不变凸函数。

同理，定理5和定理6的条件也可以削弱，得到如下的结论。

定理7f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f上半连续且满足条件A；

2)条件Ⅱ：如果对∀x,y∈K，f(x)≠f(y)，都∃γ∈(0,1)使得f(y+γα(x,y)η(x,y))<(1-γ)f(y)+γf(x)。

定理8f是K上的严格α-预不变凸函数当且仅当下面的条件成立：

1)条件Ⅰ：f下半连续且满足条件A；

2)条件Ⅱ：如果对∀x,y∈K，f(x)≠f(y)，都∃λ∈(0,1)使得f(y+λα(x,y)η(x,y))<(1-λ)f(y)+λf(x)。

3结束语

严格预不变凸函数是严格α-预不变凸函数的一种特殊的情形。本文将严格预不变凸函数的一些结果[2,8]推广到严格α-预不变凸函数，只考虑在中间点的严格α-预不变凸和一定条件下，简化了一些证明过程，在一定程度上弱化了一些条件，从而为检验一个函数是不是严格α-预不变凸函数提供了一些方便方法。

参考文献

[1]Yang X M,Li D.On Properties of Preinvex Punctions[J].Journal of Mathematical Analysis and Applications，2001，256(1):229-241.

[2]Peng J W,Yang X M.Two Properties of Strictly Preinvex Functions[J].Operations Research Transactions，2005，9(1):37-42.

[3]Yang X M,Li D.Semistrictly Preinvex Functions[J].Journal of Mathematical Analysis and Applications，2001,258:287-308.

[4]Noor M A,Noor K I.Some characterizations of strongly preinvex functions[J].Journal of Mathematical Analysis and Applications,2006,316:697-706.

[5]王美霞.α-预不变凸函数[D].天津:河北工业大学,2007:7-11.

[6]王海英,符祖峰.半严格α-预不变凸函数的一些性质[J].安顺学院学报，2012,14(3):130-132.

[7]Liu C P.Some Characterizations and Applications on Stronglyα-Preinvex and Stronglyα-Invex Functions[J].Journal of Industrial and Management Optimization,2008,4(4):727-738.

[8]庞君乾,吴惠仙.严格预不变凸函数判别准则的注记[J].杭州电子科技大学学报,2007,27(2):96-98.

[9]Yang J,Yang X M.Two New Characterizations of Preinvex Functions[J].Dynamics of Continuous，Discrete and Impulsive Systems Series B：Applications & Algorithms,2012,19(3):405-410.

[10]Oveisiha M,Zafarani J.Vector optimization problem and generalized convexity[J].Journal of Global Optimization,2012,52(1):29-43.

[11]Tang W M.On Strictly and Semistrictly Quasiα-Preinvex Functions[J].Journal of Computational Analysis and Applications,2013,15(8):1391-1402.

Some Properties of Strictlyα-Preinvex Functions

Wang Haiying，Fu Zufeng

(DepartmentofMathematicsandPhysics，AnshunUniversity，AnshunGuizhou561000，China)

Abstract：In this paper，we firstly give some characterizations of strictly α-preinvex functions under intermediate-point strictly α-preinvex for α-preinvex functions，semistrictly α-preinvex functions，upper semicontinuous functions and lower semicontinuous functions.Secondly，through the weakened consistency condition ofγ∈(0,1)，in the relatively weaker conditions，we also obtain the same conclusion.

Key words：strictly α-preinvex function;α-preinvex function；semistrictly α-preinvex function；semicontinuous function

中图分类号：O224

文献标识码：A

文章编号：1001-9146(2015)06-0080-05

作者简介：王海英(1982-)，女，河南南阳人，副教授，非线性泛函分析和最优化理论.

基金项目：国家自然科学基金资助项目(61304146)；贵州省高校优秀科技创新人才支持计划资助项目(黔教合KY字[2012]101号)；贵州省科技厅、安顺市政府、安顺学院三方联合基金资助项目(黔科合J字LKA[2013]19号)

收稿日期：2015-03-16

DOI：10.13954/j.cnki.hdu.2015.06.017