一类张量特征值互补问题的分式规划等价形式

熊高峰，凌　晨

(杭州电子科技大学理学院，浙江 杭州 310018)



一类张量特征值互补问题的分式规划等价形式

熊高峰，凌晨

(杭州电子科技大学理学院，浙江 杭州 310018)

摘要：提出了一类与非线性微分包含问题密切相关的张量高次特征值互补问题。研究了此类张量高次特征值互补问题与一类齐次多项式分式规划的等价关系，为进一步设计算法提供了一条有效途径。在此基础上，得到了一个关于张量高次特征值互补问题解的存在性结果。

关键词：高阶张量；高次特征值互补问题；分式规划；稳定点

0引言

矩阵特征值互补问题是一类特殊的非线性互补问题，它有广泛的应用背景[1-2]。一类重要形式是矩阵二次特征值互补问题，其特征值满足具有特殊结构的二次方程[3]。利用此特点，可构造出合适的非线性函数，并在相关矩阵满足所谓的co-regular和co-hyperbolic条件下，求解矩阵二次特征值互补问题可被转化成某一变分不等式的求解[3]。张量是矩阵的推广，一个与此相关的问题是张量高次特征值互补问题。与矩阵特征值互补问题类似，一类非线性微分包含问题可被等价转化成张量高次特征值互补问题。但由于其特征值高次形式的出现，使得张量高次特征值互补问题的求解成为一个困难问题。本文针对一类张量高次特征值互补问题，研究了相应的齐次多项式分式规划等价形式，并在此基础上得到互补问题的一个解的存在性结果，这为进一步研究相关数值算法设计，提供了一条有效途径。

1问题描述及相关预备知识

本文考虑一类张量特征值互补问题，即求λ∈R和非零向量x=(x1,…,xn)T∈Rn，使得：

(1)

式中,A,B,C∈Sm,n，向量x≥0意指其分量均非负。称满足式(1)的(λ,x)为张量m次特征值互补问题的特征对。若取m=2，则上述问题即为矩阵情形的二次特征值互补问题，其等价转化与解的存在性结果，见文献[3]。

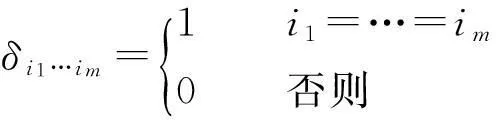
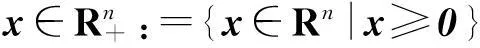
2主要结果

(2)

(3)

式(2)中，diag(y)表示以y的分量为主对角元的对角矩阵。

考虑分式规划：

(4)

(5)

将式(3)代入式(5)中第二式，得：

(6)

(7)

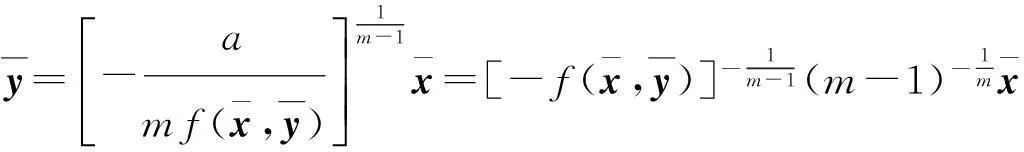
(8)

所以，有：

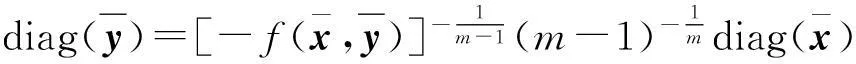
(9)

下面研究张量特征值互补问题(1)和分式规划(4)的关系。

(10)

(11)

(12)

另一方面，根据式(7)和式(10)，知：

(13)

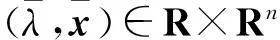
(14)

另一方面，根据式(3)和式(7)，得：

(15)

张量高次特征值互补问题解(特别是最大互补特征值λ)的计算是一个困难问题。现在，通过研究与原问题等价的齐次多项式分式规划，可为进一步设计相关(近似)算法提供一条有效途径。

众所周知，在一定条件下，矩阵情形的特征值互补问题和张量情形下的一次特征值互补问题的解均存在[1,2,7]。下面讨论张量m次特征值互补问题(1)解的存在性。

定理3设A,B,C∈Sm,n。若A为严格协正定张量，C=-I,则互补问题(1)的解必存在。

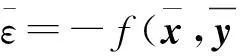
3结束语

本文研究了张量高次特征值互补问题及相应的齐次多项式分式规划等价形式。在此基础上，进一步得到了一个关于对称张量m次特征值互补问题解的存在性结果。针对对称张量的m次特征值互补问题，利用本文所得的齐次多项式分式规划等价形式，可为进一步设计相关(近似)数值算法提供一条有效途径。一般(非对称)张量的高次特征值互补问题解的存在性和算法设计将是今后研究的主要内容。

参考文献

[1]Queiroz M,Júdice J,Humes C.The symmetric eigenvalue complementarity problem[J].Mathematics and Computer Science,2003,73(248):1849-1863.

[2]Júdice J J,Sherali H D,Ribeiro I M.The eigenvalue complementarity problem[J].Computational Optimization and Applications,2007,37(2):139-156.

[3]Fernandes L M,Júdice J,Fukushima M,et al.On the symmetric quadratic eigenvalue complementarity problem[J].Optimization Methods and Software,2014,29(4):751-770.

[4]Chang K C,Pearson K,Zhang T.On eigenvalue problems of real symmetric tensors[J].Journal of Mathematical Analysis and Applications,2009,350(1):416-422.

[5]Qi L Q.Eigenvalues of a real supersymmetric tensor[J].Journal of Symbolic Computation,2005，40(6):1302-1324.

[6]Qi L Q.Symmetric nonnegative tensors and copositive tensors[J].Linear Algebra and its Applications,2013,439(1):228-238.

[7]Song Y S,Qi L Q.Eigenvalue analysis of constrained minimization problem for homogeneous polynomial[J].Journal of Global Optimization,published online on 14 August 2015,DOI 10.1007/s10898-015-0343-y.

[8]王宜举,修乃华.非线性最优化理论与方法[M].北京:科学出版社,2012:127-141.

An Equivalent Fractional Programming Form of a Class of Tensor Eigenvalue Complementarity Problems

Xiong Gaofeng，Ling Chen

(SchoolofScience，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract：This paper proposes a class of tensor higher-degree eigenvalue complementarity problems，which have closely relationship with a class of nonlinear differential inclusion problems.The equivalent connection between the considered tensor higher-degree eigenvalue complementarity problems and the corresponding homogeneous polynomial fractional programming is studied，which provides an effective method for the design of the related algorithms.Based upon this，a result on existence of solution for tensor eigenvalue complementarity problems is proved.

Key words：higher-order tensor；higher-degree eigenvalue complementarity problem；fractional program；stationary point

中图分类号：O221.2

文献标识码：A

文章编号：1001-9146(2015)06-0075-05

通信作者：

作者简介：熊高峰(1986-)，女，河南正阳人，在读研究生，非线性优化.凌晨教授，E-mail：macling@hdu.edu.cn.

基金项目：国家自然科学基金资助项目(11171083，11571087)；浙江省自然科学基金资助项目(LZ14A010003)

收稿日期：2015-03-27

DOI：10.13954/j.cnki.hdu.2015.06.016