平面多边形增减顶点时中值坐标的计算

朱方妍，张善奎，邓重阳

(杭州电子科技大学理学院,浙江 杭州 310018)

摘要：中值坐标是定义在任意平面多边形上最常用的重心坐标。揭示了增减平面多边形的顶点时，多边形所在平面内点的中值坐标的变化情况，即当多边形减少或增加一个顶点时，则除去所增减的点以及它的两个相邻点外，其余各点对应的规范化中值坐标变为原来的常数倍。

关键词：推广的重心坐标;中值坐标；平面多边形

DOI: 10.13954/j.cnki.hdu.2015.01.022

平面多边形增减顶点时中值坐标的计算

朱方妍，张善奎，邓重阳

(杭州电子科技大学理学院,浙江 杭州 310018)

摘要：中值坐标是定义在任意平面多边形上最常用的重心坐标。揭示了增减平面多边形的顶点时，多边形所在平面内点的中值坐标的变化情况，即当多边形减少或增加一个顶点时，则除去所增减的点以及它的两个相邻点外，其余各点对应的规范化中值坐标变为原来的常数倍。

关键词：推广的重心坐标;中值坐标；平面多边形

DOI:10.13954/j.cnki.hdu.2015.01.022

收稿日期：2014-06-16

基金项目：国家自然科学基金资助项目(61370166)

通信作者：

作者简介：朱方妍(1991-)，女，河南商丘人，在读研究生，计算数学.邓重阳副教授，E-mail: dcy@hdu.edu.cn.

中图分类号：O24

文献标识码：：A

文章编号：：1001-9146(2015)01-0104-03

Abstract:Mean value coordinates are the most commonly barycentric coordinates defined in arbitrary planar polygon. This paper reveals how the coordinates of the interior point in a planar polygon change as the vertexes are increased or decreased， namely， when the polygon reduces or increases a vertex， except the increased or decreased and its two adjacent points， the rest values of the normalized coordinates at the corresponding points turn into a constant multiple of the original.

0引言

定义在三角形上的重心坐标可以将三角形所在平面内的任意点唯一地表示为三角形三个顶点的线性组合，所以广泛应用于计算机图形学、几何造型、地形建模和有限元[1]等领域。近年来，涌现出很多类型的重心坐标，使之推广到任意多边形乃至多面体，如调和坐标[2]、中值坐标[3]、复数坐标[4]、矩阵坐标[5]、泊松坐标[6]以及局部坐标[7]。其中最成功的方法当属Floater提出的中值坐标[8-10]，因为其具有适用于平面任意多边形、在多边形平面内任意一点都有定义、无穷阶连续、计算稳定等优良特性。

在计算机动画设计和几何造型等领域中，为了设计出所需的形状，常常要在已有多边形的基础上增加或者减少顶点。在增减顶点后，如果所有的中值坐标全部重新计算，必然会导致很大的计算量。本文揭示了增减平面多边形的顶点时，多边形所在平面内点的中值坐标的变化情况，即当多边形减少或增加一个顶点时，则除去所增减的点以及它的两个相邻点外，其余各点对应的规范化中值坐标变为原来的常数倍。这样可以大大减少后续的计算量。

1多边形在增减顶点时中值坐标的变化

1.1　减少一个顶点

如图1所示，记多边形Ψ的顶点为v1，v2，…，vn，ri(v)为vi到v的欧几里得距离，αi(v)表示三角形[v，vi，vi+1]在顶点v处的有向角，则点v相对多边形Ψ的各个顶点的齐次中值坐标函数[9]为：

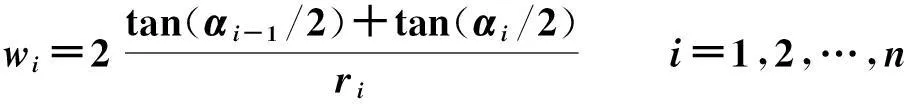
(1)

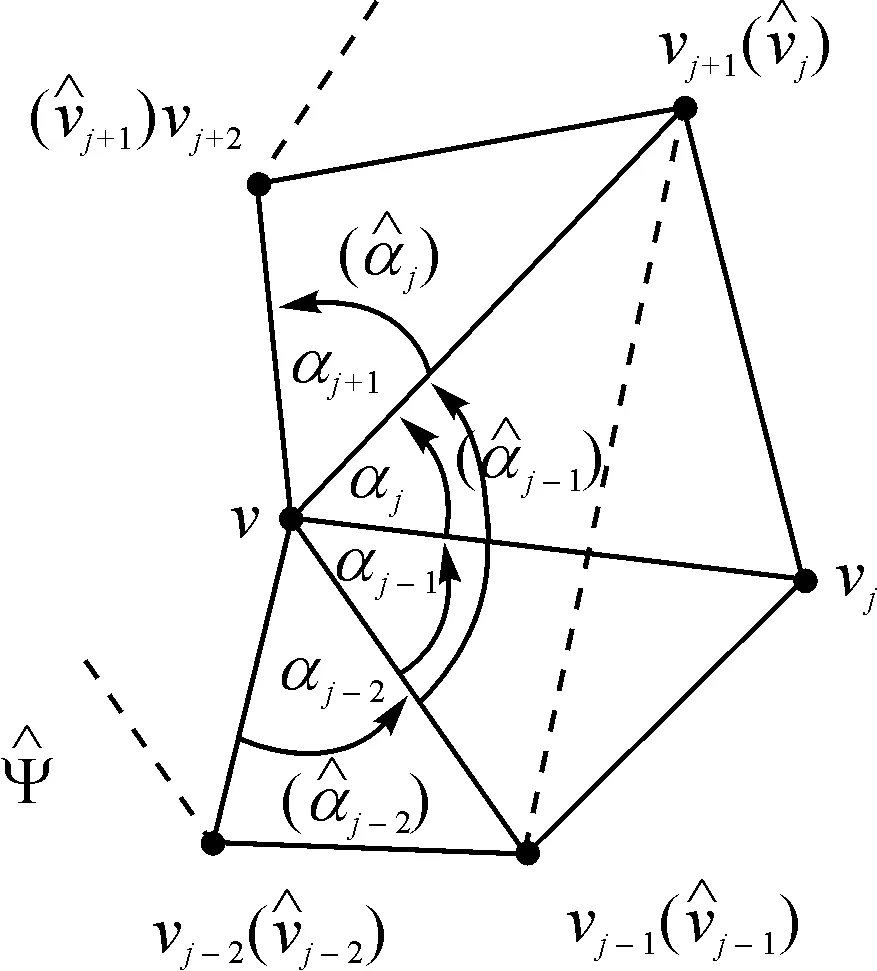
图1　减少多边形的一个顶点

(2)

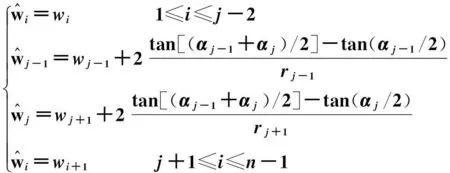
(3)

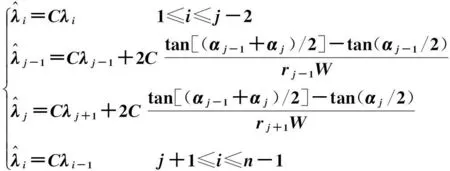
(4)

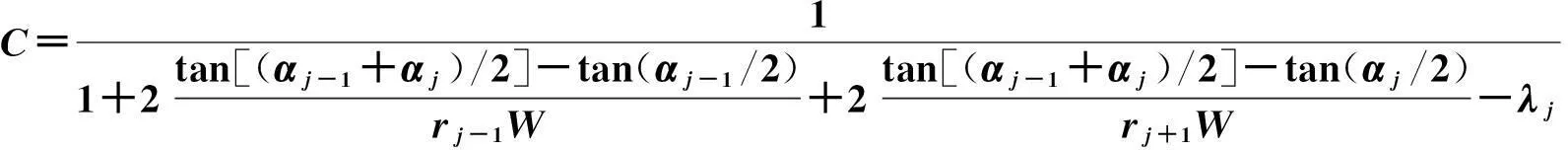
从上述关系式可以看出，多边形Ψ减少一个顶点vj之后，除了点vj的相邻点vj-1和vj+1外，其余各点对应的规范化中值坐标与原来的相比只相差一个常数倍。

1.2　增加一个顶点

增加新点可以分为新点在边上或不在边上这两种情况，前一种情况已有定论(参见文献[9])，这里只考虑第二种情况。

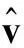
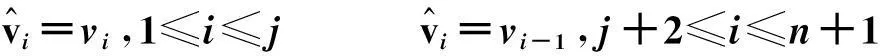
(5)

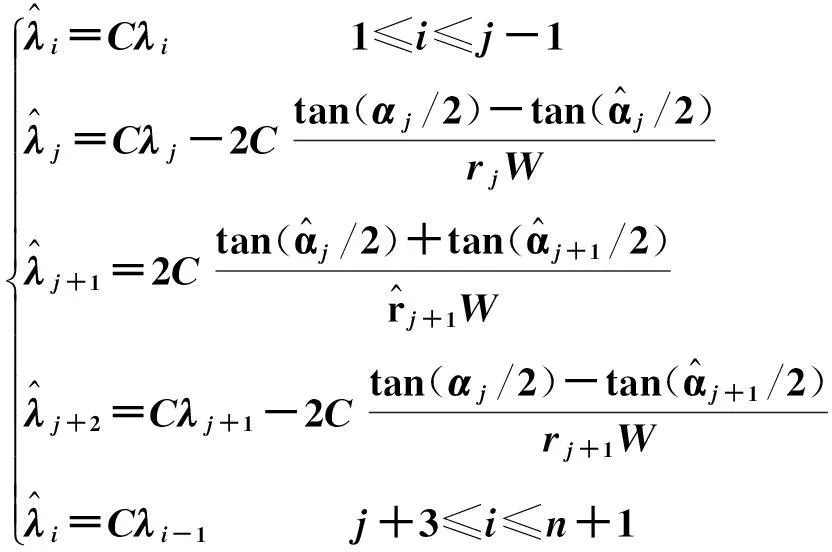
(6)

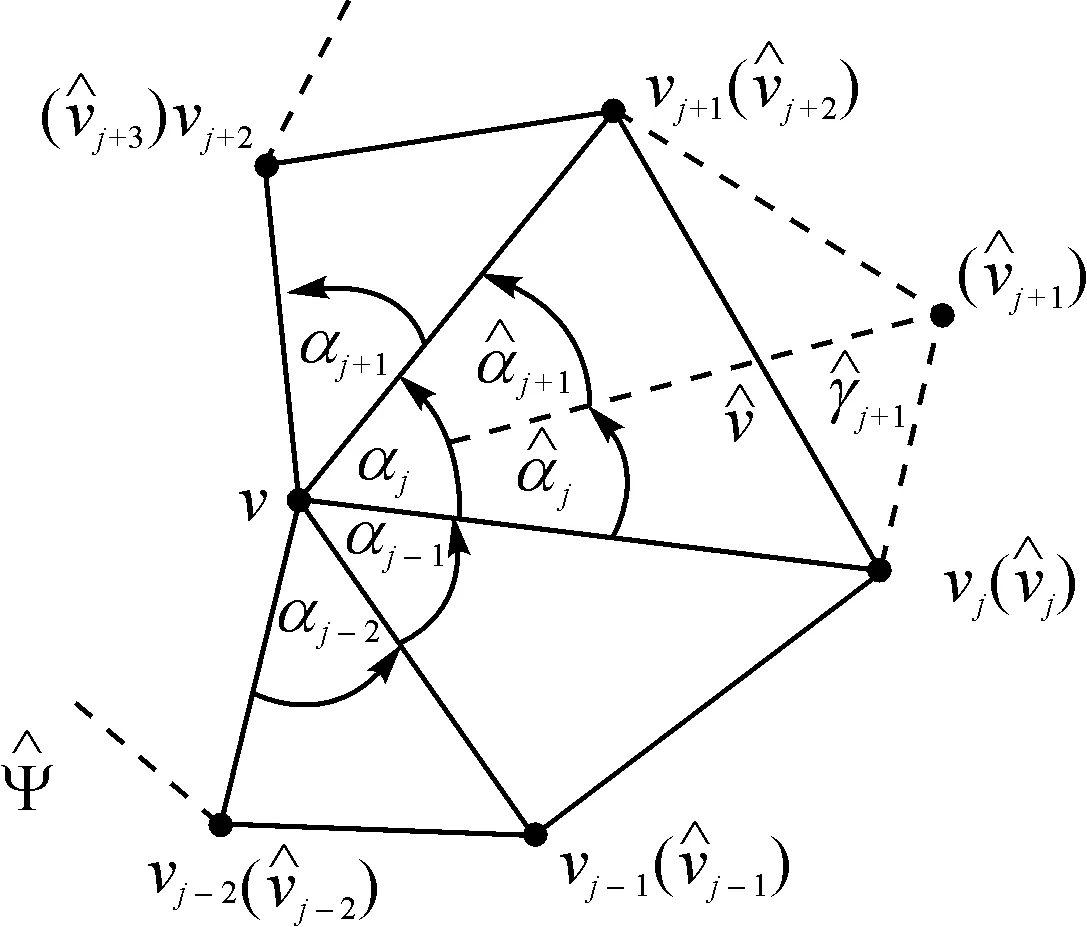
图2　增加多边形的一个顶点

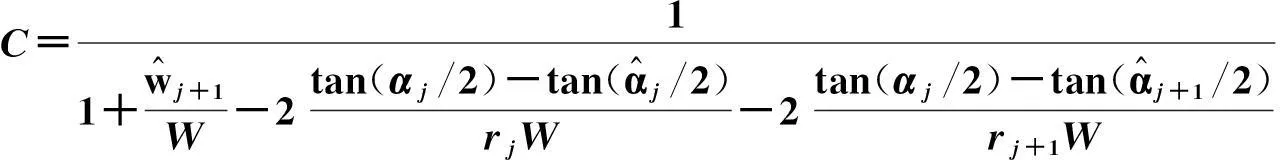
2数值例子

取多边形边数为n=10，多边形的顶点坐标x0=[0.400 4，0.607 4，0.806 6，0.896 5，0.646 5，0.419 9，0.162 1，0.322 3，0.150 4，0.193 4]，y0=[0.962 8，0.956 1，0.848 0，0.543 9，0.003 4，0.091 2，0.077 7，0.327 7，0.523 6，0.848 0]。

然后，在该多边形内任取一点(x，y)=(0.537 1，0.543 9)的关于此多边形的重心坐标λ1=[0.073 3，0.079 3，0.112 7，0.219 6，0.118 3，0.059 3，0.027 9，0.089 5，0.127 8，0.092 4]。

去掉第4个顶点后，得到九边形的重心坐标λ2=[0.063 6，0.068 8，0.304 5，0.219 0，0.051 5，0.024 2，0.077 6，0.110 8，0.080 1]。在第4和第5个顶点之间加上一个新顶点(0.959 0，0.091 2)后，得到十一边形的重心坐标λ3=[0.077 5，0.083 9，0.119 2，0.162 1，0.076 3，0.061 2，0.062 8，0.029 5，0.094 6，0.135 2，0.097 7]。

通过计算，除了减少的顶点和此顶点的两个相邻点之外，其余顶点对应的中值坐标与原来比值均为0.867 4，除了增加的顶点和此顶点的两个相邻点外，其余顶点对应的中值坐标与原来的比值为1.057 7。

以上数值模拟实验说明，理论分析与实验模拟相吻合。另外，根据多次数值模拟结果得出，对于内部点，多边形减少顶点时，它相对其余顶点的的中值坐标变为原来的m倍，其中m≤1；多边形增加顶点时，它相对其余顶点的中值坐标变为原来的n倍，其中n≥1。对于外部点，中值坐标的变化情况正好与此相反。

3结束语

在形状编辑中，平面多边形增减顶点是一个非常常见的操作。通过理论分析，本文得出多边形增减顶点时，多边形所在平面内一点的中值坐标的变化规律。本文所讨论算法可以有效地提高图形编辑中所涉及的数值计算的效率。

参考文献

[1]Wachspress E L. A Rational Finite Element Basis[M]. Burlington： Elsevier，1975：88-125.

[2]Joshi P， Meyer M， DeRose T， et al. Harmonic coordinates for character articulation[J]. ACM Transactions on Graphics(TOG)，2007，26(3):71.

[3]Floater M S. Mean value coordinates[J]. Computer Aided Geometric Design，2003，20(1):19-27.

[4]Weber O， Ben-Chen M，Gotsman C.Complex Barycentric Coordinates with Applications to Planar Shape Deformation[J]. Computer Graphics Forum，2009，28(2):587-597.

[5]黄力慰，李桂清，熊赟晖.矩阵重心坐标[J].计算机辅助设计与图形学学报，2011，23(12):1 959-1 966.

[6]Li X Y， Hu S M. Poisson coordinates[J]. IEEE Transactions on Visualization and Computer Graphics，2013，19(2):344-352.

[7]Zhang J Y， Deng B L， Liu Z S， et al. Local Barycentric Coordinates[J]. ACM Transactions on Graphics， 2014，33(EPFL-ARTICLE-201 853).

[8]Ju T， Schaefer S， Warren J. Mean value coordinates for closed triangular meshes[J]. ACM Transactions on Graphics(TOG)，2005，24(3):561-566.

[9]Hormann K， Floater M S. Mean value coordinates for arbitrary planar polygons[J]. ACM Transactions on Graphics(TOG)，2006，25(4):1 424-1 441.

[10]Bruvoll S， Floater M S. Transfinite mean value interpolation in general dimension[J]. Journal of Computational and Applied Mathematics，2010，233(7):1 631-1 639.

Calculation of Mean Value Coordinates in Process of

Planar Polygon Vertexes’ Decrease or Increase

Zhu Fangyan， Zhang Shankui， Deng Chongyang

(SchoolofScience，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Key words: general barycentric coordinates; mean value coordinates; planar polygon