一类关于二阶微分方程的追逐微分博弈问题
2016-01-22冯亚琴洪世煌李春红
冯亚琴,洪世煌,李春红
(杭州电子科技大学理学院,浙江 杭州 310018)
摘要:考虑一类用二阶微分方程描述的多人追逐一人逃逸的追逐微分博弈。在此博弈中,对参与者的控制函数强加上了积分约束,支付函数是博弈结束时追逐者和逃逸者之间距离的下确界。主要目的是建立可容许的追逐策略来保证博弈从任何给定的初始位置是追逐完备的。
关键词:追逐微分博弈;积分约束;策略;追逐完备
DOI: 10.13954/j.cnki.hdu.2015.01.021
一类关于二阶微分方程的追逐微分博弈问题
冯亚琴,洪世煌,李春红
(杭州电子科技大学理学院,浙江 杭州 310018)
摘要:考虑一类用二阶微分方程描述的多人追逐一人逃逸的追逐微分博弈。在此博弈中,对参与者的控制函数强加上了积分约束,支付函数是博弈结束时追逐者和逃逸者之间距离的下确界。主要目的是建立可容许的追逐策略来保证博弈从任何给定的初始位置是追逐完备的。
关键词:追逐微分博弈;积分约束;策略;追逐完备
DOI:10.13954/j.cnki.hdu.2015.01.021
收稿日期:2014-04-02
基金项目:国家自然科学基金资助项目(71471051);浙江省自然科学基金资助项目(LY12A01002)
通信作者:
作者简介:冯亚琴(1989-),女,陕西安康人,在读研究生,应用数学.洪世煌教授,E-mail: hongshh@hotmail.com.
中图分类号:O225
文献标识码::A
文章编号::1001-9146(2015)01-0101-03
Abstract:In this paper, we consider a pursuit differential game of many pursuers and one evader in Hilbert space, which is described by the second-order differential equations. In process of the game, control functions of the players are subjected to integral constraints, the payoff function is the greatest lower bound of distances between the pursuers and evader when the game is terminated. The main result of this paper is to constructing the admissible strategies of the pursuers to guarantee the completion of pursuit from any given initial position in the game.
0引言
追逐微分博弈问题是如何建立可容许的追逐策略引导一个或一组追逐者捕捉一个移动逃逸目标,具有广泛的应用价值,同时又是博弈理论的热点问题,国内外学者针对它已经做了大量的研究。例如,关于用一阶微分方程描述的追逃微分博弈[1-4],对局中人的控制函数都强加上了积分约束的条件,最终建立最优追逐策略或者得到追逐完备的充分条件。文献[5]考虑了多个局中人的追逃微分博弈,最终建立了局中人的最优策略。为了解决这些博弈问题,通常借助一个辅助博弈即一人追逐一人逃逸的简单运动的追逐微分博弈,而本文在文献[5]的启发下,将二阶微分方程描述的追逐微分博弈转化成等价的一阶微分方程描述的追逐微分博弈,然后直接建立可容许的追逐策略来得到追逐完备的充分条件。
1预备知识
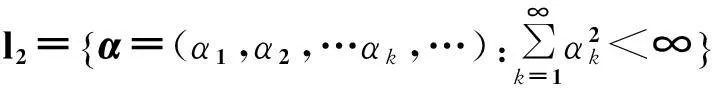
在l2空间上,考虑多个追逐者P1,P2,…,Pm和一个逃逸者E的追逐微分博弈,通过以下微分方程来描述:
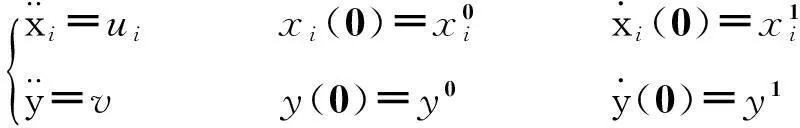
(1)
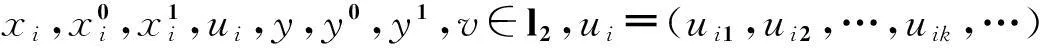
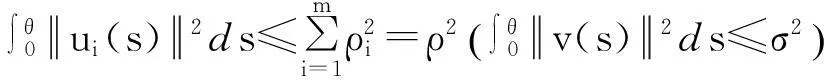
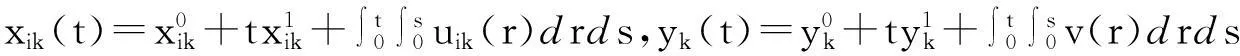
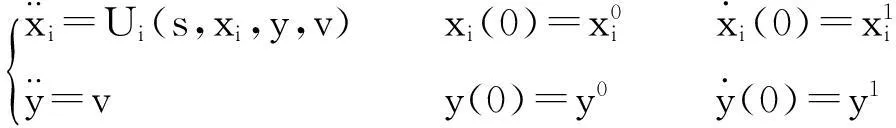
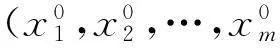
为了解决这个博弈问题,考虑一个相同支付函数的等价追逐微分博弈来替代由式(1)描述的追逐微分博弈,这个等价博弈通过下述系统方程描述:
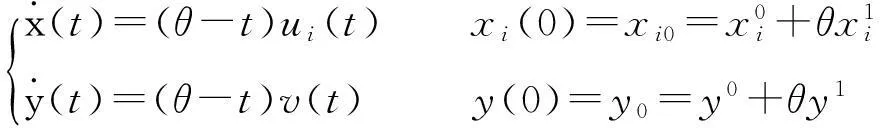
(2)
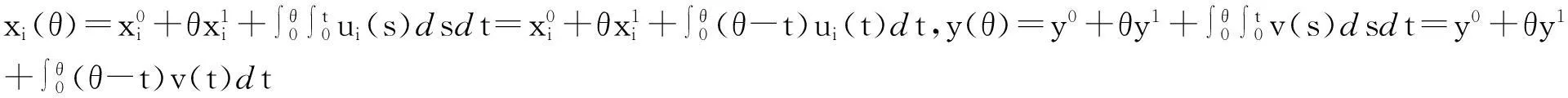
另一方面,由式(2)也可以得到上述的结果。
2主要结论
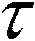
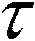
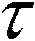
定理如果ρ2>3σ2,则博弈(2)在给定的追逐策略Ui1(t),0≤t≤θ下是追逐完备的。
证明为了证明上述定理,需讨论两种情况。
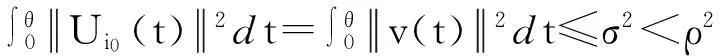
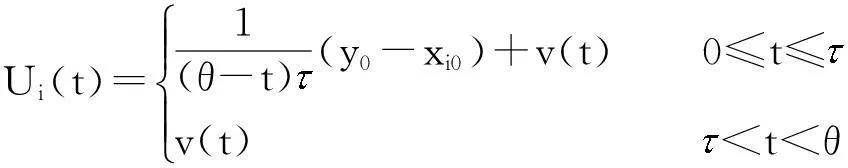

3结束语
本文在Hilbert空间上,讨论一类关于二阶微分方程的追逐微分博弈问题,通过转化的等价追逐微分博弈以及建立可容许的追逐策略得到追逐完备的充分条件。得到的结果可以看作是有限维空间中简单运动的追逐微分博弈的拓展。在此基础上,还可以进一步尝试研究由非线性微分方程描述的追逐微分博弈问题。
参考文献
[1]Ja’afaru A B, Ibragimov G I. On some pursuit and evasion differential game problems for an infinite number of first-order differential Equations[J]. Journal of Applied Mathematics,2012:1-13.
[2]Ibragimov G I. A game problem on a closed convex set[J]. Siberian Advances in Mathematics,2001,4(2):96-112.
[3]Leong W J, Ibragimov G I. A multi-person pursuit problem on a closed convex set in Hilbert space[J]. Far East Journal of Applied Mathematics,2008,33(2):205-214.
[4]Ibragimov G I, Satimov N M. A multiplayer pursuit differential game on a closed convex set with integral constraints[J]. Abstract and Applied Analysis,2012:1-12.
[5]Ibragimov G I, Salimi M. Pursuit-evasion differential game with many inertial players[J]. Mathematical Problems in Engineering,2009:1-15.
On Pursuit Differential Game Problems for
a Second-order Differential Equations
Feng Yaqin, Hong Shihuang, Li Chunhong
(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Key words: pursuit differential game; integral constraints; strategies; the completion of pursuit
