基于Keystone-FRFT的机动弱目标检测算法

郭云飞，周森山，赵尚宇

(杭州电子科技大学自动化学院，浙江 杭州 310018)

摘要：针对机动弱目标检测中出现的距离走动和多普勒频率走动问题，在分析回波信号走动的基础上，提出一种基于楔形变换和分数阶傅里叶变换的弱目标检测算法。算法使用楔形变换补偿距离走动，利用分数阶傅里叶变换补偿多普勒频率走动，在低信噪比情况下能有效地检测机动弱目标。仿真分析表明算法有效。

关键词：距离走动，多普勒频率走动，楔形变换，分数阶傅里叶变换

DOI: 10.13954/j.cnki.hdu.2015.01.020

基于Keystone-FRFT的机动弱目标检测算法

郭云飞，周森山，赵尚宇

(杭州电子科技大学自动化学院，浙江 杭州 310018)

摘要：针对机动弱目标检测中出现的距离走动和多普勒频率走动问题，在分析回波信号走动的基础上，提出一种基于楔形变换和分数阶傅里叶变换的弱目标检测算法。算法使用楔形变换补偿距离走动，利用分数阶傅里叶变换补偿多普勒频率走动，在低信噪比情况下能有效地检测机动弱目标。仿真分析表明算法有效。

关键词：距离走动，多普勒频率走动，楔形变换，分数阶傅里叶变换

DOI:10.13954/j.cnki.hdu.2015.01.020

收稿日期：2014-04-25

作者简介：郭云飞(1978-)，男，河北邯郸人，副教授，目标检测与跟踪.

中图分类号：TN957.51

文献标识码：：A

文章编号：：1001-9146(2015)01-0097-04

Abstract:For the problem of range migration and Doppler frequency migration in maneuvering weak target detection， on the basis of echo signal analysis， a maneuvering weak target detection algorithm based on Keystone transform and fractional Fourier transform(FRFT) is proposed. In this method， Keystone transform is used to correct the range migration， and FRFT is used for phase compensation. It is ideal for maneuvering target detection under low signal to noise ratio(SNR) condition， simulation results demonstrate the validity of this method.

0引言

微弱目标信号检测中，常采用相参积累的方法加大回波信号能量，提高雷达对微弱目标的检测能力。传统相参积累的使用前提是目标近似做匀速直线运动，多普勒频率为常数，通过一段时间的积累可以提高信噪比[1]。但是对于雷达机动微弱目标，由于目标可能具有强机动性，在整个积累过程中多普勒频率不再为常数，通常会产生距离走动和多普勒频率走动等问题。针对距离走动补偿问题，通常使用Hough变换、时分包络移位补偿和楔形变换(Keystone Transform)等补偿算法，Hough变换属于一种非相参积累方式，积累性能不如相参积累，时分包络移位算法运算量较大，且需要提前估计速度值，Keystone变换方法不需要提前估计速度，适用于低信噪比时的距离包络对齐[2-4]。针对多普勒频率走动补偿问题，目前有高阶模糊函数法(High-Order Ambiguity Function， HAF)、Wigner-Hough变换和分数阶傅里叶变换(Fractional Fourier Transform， FRFT)等，HAF在低信噪比目标检测中需要积累较多的脉冲，运算量较大，Wigner-Hough变换是将一维时域信号变换成二维参数分布，导致运算量增加，且存在一定的积累损失，分数阶傅里叶变换是一种广义的傅里叶变换，它属于线性时频变换，不存在交叉项干扰问题且积累增益效果良好[4-6]。结合以上现有的算法分析，本文提出了一种基于Keystone变换和FRFT的机动目标检测算法。首先分析距离走动和多普勒走动对信号的影响，通过Keystone变换补偿距离走动，在距离补偿的基础上通过FRFT补偿多普勒频率走动，仿真分析表明算法在微弱目标检测方面性能较为显著。

1回波信号模型

假设雷达发射线性调频脉冲，其数学表达式为：

(1)

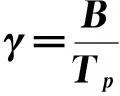
(2)

(3)

式中，p(t)为线性调频信号的频谱，f为快时间域频率值。把R(tm)代入式(3)，可得回波信号表达式为：

(4)

(5)

(6)

从式(6)可以看出，由于速度v的存在，使得其峰值随着时间的变换而产生走动，当机动目标的距离走动项超过半个距离单元则会出现距离走动。由于包含时间的二次项系数，多普勒频率不再为一个常数，因此会存在一定的多普勒扩散现象。距离走动和多普勒走动积累效果如图1所示。从图1中可以看出回波信号在距离单元和多普勒频率单元上能量产生严重扩散。

图1　距离走动和多普勒走动示意图

2回波信号走动补偿

(7)

图2为第1、10、20个脉冲的回波图，可以看出不同脉冲之间发生了距离走动，在上述距离走动分析中，加入Keystone变换，图3为距离补偿后第1、10、20个脉冲的回波图，从图3中可以看出距离走动问题得到了有效解决。

图2　不同脉冲距离走动示意图

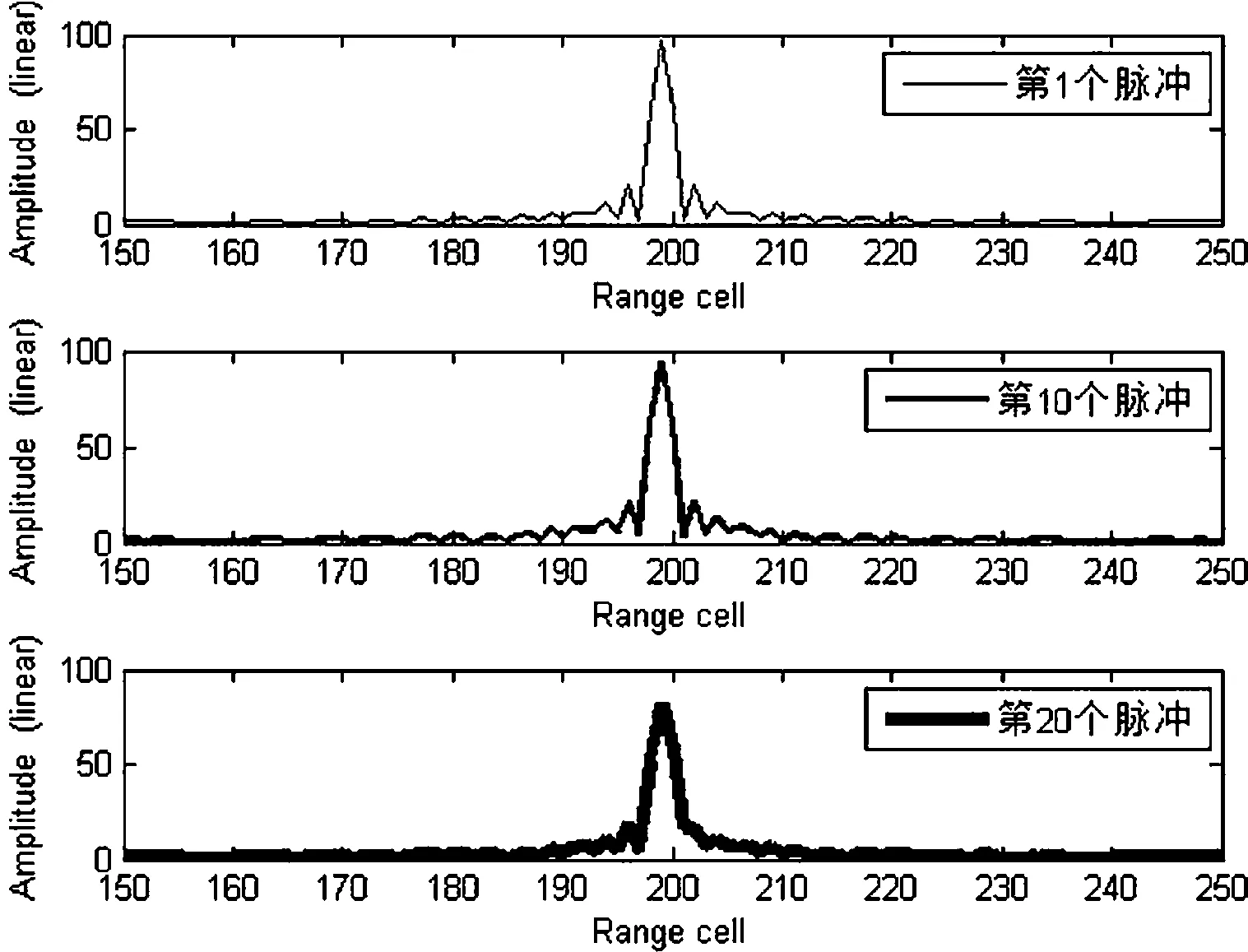
图3　不同脉冲距离走动补偿示意图

根据式(5)可知，经过长时间脉冲积累后，信号的多普勒回波可以用多项式相位信号模型来描述，其多普勒频率在慢时间域近似为LFM信号[9]。FRFT把LFM信号在不同阶次上进行能量集聚，这时可以采用FRFT对其进行检测，其FRFT公式定义为[10]：

(8)

3仿真分析

假设雷达发射信号的载频为3 GHz，脉冲重复频率1 kHz，积累脉冲数128，基带线性调频信号带宽1 MHz，脉冲宽度0.1 ms，单个脉冲信噪比-5 dB，速度为1 000 m/s，加速度为40 m/s2。如图4(a)所示，使用Keystone变换和传统的动目标检测技术(Moving Target Detection， MTD)并不能有效补偿多普勒频率走动问题，由于多普勒频率维展宽，积累增益受到了严重影响。Keystone+FRFT算法如图4(b)所示，在距离补偿的同时利用FRFT进行多普勒频率走动补偿，回波信号呈现出明显尖峰，回波信号能量得到有效聚集。图4(a)中积累增益约为1×104dB，图4(b)中积累增益约为1.5×104dB，比较图4(a)、图4(b)可以看出，回波信号的积累增益得到了有效提高。

图4　不同算法比较(SNR=-5 dB)

把信噪比从-5 dB降低到-15 dB，从图5(a)中可以看出，Keystone+MTD算法检测效果较差。从图5(b)中可以看出，在低信噪比条件下，Keystone+FRFT算法依然可以对距离走动、多普勒频率走动进行有效补偿，证明了该算法在信噪比降至一定程度下依然具有良好的检测性能。

图5　不同算法比较(SNR=-15 dB)

4结束语

影响雷达检测性能的主要因素是脉冲回波出现的距离走动和多普勒频率走动问题，本文提出了一种基于Keystone变换和FRFT的运动目标检测算法，通过Keystone变换补偿距离单元走动，然后，利用FRFT进行相位补偿，校正多普勒频率走动，通过仿真验证了低信噪比情况下，该算法具有良好的检测性能。另外，本文的目标运动背景只考虑了匀加速运动，实际应用中，随着积累时间的延长，目标有可能做变加速、转弯等复杂机动飞行。因此，继续寻找有效的机动弱目标检测算法，具有较深的实际意义。

参考文献

[1]徐冠杰.雷达信号长时间积累对微弱目标检测的研究[D].西安：西安电子科技大学，2011:2-3.

[2]田超，文树梁.基于非均匀FFT的长时间相参积累算法[J].电子与信息学报，2014，36(6)：1374-1 380.

[3]张顺生，曾涛.基于Keystone变换的微弱目标检测[J].电子学报，2005，33(9)：1 675-1 678.

[4]夏卓卿，陆军，陈伟建.凝视动目标相参积累技术研究[J].中国电子科学研究院学报，2009，4(5)：498-502.

[5]李海，吴嗣亮，莫力.微弱信号长时间积累的检测方法[J].北京理工大学学报，2001，21(5)：614-617.

[6]张南，陶然，王越.基于变标处理和分数阶傅里叶变换的运动目标检测算法[J].电子学报，2010，38(3)：683-687.

[7]战立晓，汤子跃、朱振波.基于Keystone变换和MDCFT的高机动弱目标检测与参数估计[J].航空学报，2013，34(4)：855-863.

[8]蒋千.高速目标雷达信号长时间积累技术研究[D].成都：电子科技大学，2013:39-41.

[9]陈小龙，关键，黄勇，等.分数阶Fourier变换在动目标检测和识别中的应用：回顾和展望[J].信号处理，2013，29(1)：85-97.

[10]陶然，齐林，王越.分数阶Fourier变换的原理与应用[M].北京：清华大学出版社，2004:3.

[11]战立晓，汤子跃，朱振波.基于分数阶傅里叶变换的加速微弱目标检测与估计[J].电波科学学报，2013，28(2)：296-304.

[12]王娟，赵永波.Keystone变换实现方法研究[J].火控雷达技术，2011，40(1)：45-51.

[13]Ozaktas H， Arikan O， Kutay M. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing，1996，44(9):2 141-2 150.

A Maneuvering Weak Target Detection Algorithm

Based on Keystone-FRFT

Guo Yunfei， Zhou Senshan， Zhao Shangyu

(SchoolofAutomation，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Key words: range migration; Doppler frequency migration; Keystone transform; fractional Fourier transform