三明治结构的特异材料板间相对Casimir力的研究

肖　楠，曾　然，李齐良

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

摘要：微型机械的尺寸缩小至微纳米范围使得Casimir效应对微纳米系统的影响不容忽视。基于Lifshiftz理论，着手研究了三明治结构的特异材料板间的相对Casimir力，即考虑在有无色散情况下三明治结构的特异材料板间Casimir力的比值。研究分析了影响相对Casimir力的因素，包括金属板的间距、特异材料板厚度以及特异材料的填充因子等，还引入了Casimir力的幅度问题，一并来调控Casimir力，应用于工业生产。

关键词：相对卡西米尔力；特异材料；卡西米尔力幅度

DOI: 10.13954/j.cnki.hdu.2015.01.015

三明治结构的特异材料板间相对Casimir力的研究

肖楠，曾然，李齐良

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

摘要：微型机械的尺寸缩小至微纳米范围使得Casimir效应对微纳米系统的影响不容忽视。基于Lifshiftz理论，着手研究了三明治结构的特异材料板间的相对Casimir力，即考虑在有无色散情况下三明治结构的特异材料板间Casimir力的比值。研究分析了影响相对Casimir力的因素，包括金属板的间距、特异材料板厚度以及特异材料的填充因子等，还引入了Casimir力的幅度问题，一并来调控Casimir力，应用于工业生产。

关键词：相对卡西米尔力；特异材料；卡西米尔力幅度

DOI:10.13954/j.cnki.hdu.2015.01.015

收稿日期：2014-05-09

基金项目：浙江省自然科学基金资助项目(LY14A040008,Y1110078)

作者简介：肖楠(1988-)，女，江苏盐城人，在读研究生，含特异材料多层结构的Casimir力的研究.

通信作者：曾然副教授，E-mail: zengran@hdu.edu.cn.

中图分类号：TN04

文献标识码：：A

文章编号：：1001-9146(2015)01-0075-04

Abstract:The size of the micromachine reduces to micron and nanometer， and it makes that the Casimir effect can not be ignored. Based on the Lifshiftz theory， we do the research on relative Casimir force between the metamaterials slabs of sandwich structure and study the ratio whether the dispersion is taken into account or not. At the same time， we analyze the influence factors of relative Casimir force， including the separation of the metal slabs， the thickness of the metamaterials slab and the filling factor of the metamaterials slab etc， these are cited with amplitude of Casimir force to control the Casimir force to apply in industrial production.

0引言

1948年Casimir在理论上推导出真空中靠的很近的两个中性理想导体板间存在相互吸引力[1]，这就是著名的Casimir效应，它在物理学领域占有重要地位，尤其对纳米技术、微电子技术等应用有重要影响。Casimir吸引力引起的粘滞作用给工业生产造成麻烦，而Casimir排斥力则可以使量子悬浮，所以人们致力研发具有零或者排斥性的Casimir力系统。Boyer指出可通过一块理想导体板和一块具有无限大磁导率的材料板获得Casimir排斥力[2]。随着特异材料的发展，可获得具有强磁响应的材料，这为Casimir排斥力的实现提供了条件，人们将介质材料板间Casimir力的研究拓展到涉及特异材料的情况[3]。所谓特异材料，它是一种新型的人工结构，其介电系数和磁导率可同时为负值，也可其中之一为负值，或者同时小于1[4]。特异材料的巨大应用前景源于它的制造实现，比如用它来制造“超透镜”，超透镜是一种能突破衍射极限分辨率成像的纳米透镜，其设计思路就是基于特异材料[5]。Casimir力的测量是一个非常复杂的问题，因为在1μm或者更短距离内控制宏观物体很困难，另外测量时还要考虑材料表面粗糙程度、材料表面间距等。直至2002年，G.Bressi等人对两个平行板结构的Casimir力进行了测量，实验的精确度也只有15%[6]。本文从理论上研究三明治结构实现的可能性，对实际空间结构的Casimir力进行了考察。基于Lifshiftz理论计算了三明治结构的特异材料板间相对Casimir力，研究分析了影响相对Casimir力的因素，得出了相关结论。

1三明治结构的特异材料板间相对Casimir力

相对Casimir力η=F2/F1，其中F1为无色散时结构板间的Casimir力，F2为考虑色散时结构板间的Casimir力。三明治结构如图1所示，A为金属金板，B为金属银板，A、B厚度约为0.5 μm，在两板间加入一特异材料板，B′为通过特异材料板的成像。

假设一特异材料板，其介电系数和磁导率取值ε=μ=1，即没有考虑材料色散对Casimir力的影响，对于Casimir腔本文采用标准结论[1]，其单位面积的Casimir力为：

(1)

研究表明，加入特异材料板后，可以使吸引力转化成排斥力。考虑特异材料板的色散时，三明治结构板间的Casimir力表示为[8]：

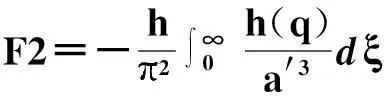
(2)

式中，板间距的有效距离a′=a-b+b/ε(iξ)，q和h(q)分别满足：

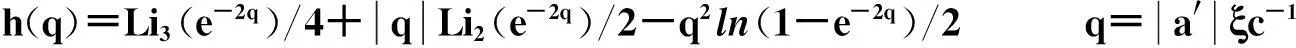
(3)

这里，取介电系数与磁导率相等，以下两种为例进行分析。

1)色散特性采用Drude-Lorentz模型来描述[9]：

(4)

2)介电常数是单共振模型叠加一个Drude背景[9]：

(5)

式中，ΩD=Ω和γD=0.006 Ω是特异材料中的金属成分的Drude参数，f是金属成分在材料中占的体积比，即材料的填充比例因子。

计算Casimir力的公式不一，文献[10]中，涉及到Casimir力的另一表示法：

(6)

式中，α是介质板结构常数，vL，R是左右介质板的Landau-level填充因子，d为左右两介质板间距。与式(1)相比，FCasimir∝α2，Casimir力的幅度明显受到了α2的抑制。

2仿真与结果分析

依据式(4)、式(5)做出的特异材料板的色散关系如图2所示。由图2可看出，频率与材料的填充比例因子通过影响材料的介电系数，从而影响相对Casimir力。

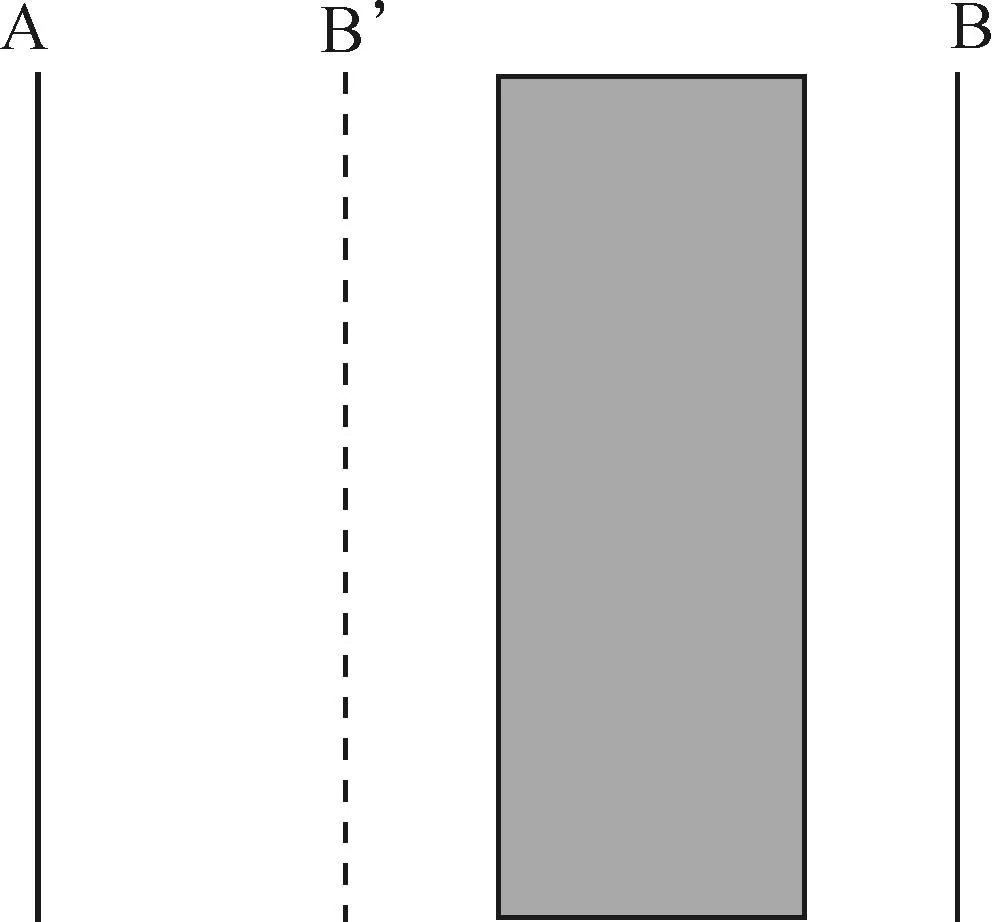
图1　三明治结构的特异材料板模型图

图2　三明治结构的特异材料板的色散关系图

介电系数根据式(4)、式(5)所得不同值，其相对Casimir力(η=F2/F1)随距离a的关系分别如图3(a)、(b)所示，其他参数如图2。从图3(a)中可以看出，板间距a对相对Casimir力产生显著的影响。在其他参数都相同条件下，对于积分的贡献，有一部分频段的贡献是吸引力的贡献，另一部分频段贡献是排斥力贡献，最终积分的总结果是它们贡献的合成，即随着板间距的增大，Casimir力逐渐减小且向零逼近，说明板间距增大对Casimir力起了减弱作用。

图3(b)则显示了电磁特异材料的填充因子f的大小对相对Casimir力的影响，可以看出填充比例因子f的大小直接影响相对Casimir力，f越小相对Casimir排斥力贡献越强。当f变大时，即电磁特异材料中金属结构所占比例增大，Casimir排斥力贡献逐渐减弱，吸引力贡献在增强，最终结果是它们贡献的合成。

图3　对应不同介电系数，相对Casimir力与距离a的关系图

材料的电磁参数不变时，相对Casimir力(η=F2/F1)受特异材料板厚度b的变化情况如图4所示。取特异材料板的厚度b=3，b=4，b=5，参照式(5)，作出相对Casimir力与板间距a的关系图，从图4中看出，b对相对Casimir力产生显著的影响。根据Casimir力η=F2/F1知，F1跟b无关，b只影响F2，从而影响相对Casimir力。

图4　不同厚度的特异材料板与三明治结构间的相对Casimir力的关系图

参考式(6)，类推介质板结构加入特异材料板后，Casimir力幅度必受到影响，取a=4，在介电系数为式(4)情况下，得到F1=0.003，F2=5.035×1 020，明显的特异材料板的介电系数加强了Casimir力的幅度大小，这个结果可以用于调控Casimir力的幅度大小。

3结束语

基于Lifshiftz理论，本文对三明治结构的特异材料板间的Casimir力进行了研究。分析了影响结构板间Casimir力的因素，包括特异材料板的间距、板厚度以及特异材料的填充因子等。本文还引入了Casimir力幅度问题，一并来调控相对Casimir力，以获得排斥性的Casimir力系统应用于微机电结构，使其更加趋于稳定，这对微型机械的发展具有非常积极的意义。

参考文献

[1]Casimir H B G. On the attraction between two perfectly conducting plates[C]//Proc. K. Ned. Akad. Wet.1948，51(793):150.

[2]Boyer T H. Van der Waals forces and zero-point energy for dielectric and permeable materials[J]. Physical Review A，1974，9(5):2 078.

[3]Ma J， Zhao Q， Meng Y. Magnetically controllable Casimir force based on a superparamagnetic metametamaterial[J]. Physical Review B，2014，89(7):75 421.

[4]许静平，羊亚平，陈鸿.特异材料与卡西米尔(Casimir)效应[J].科学通报，2011，56(13):985-994.

[5]易翎杰.基于负折射率材料的超级透镜成像研究[D].成都:电子科技大学，2011:8-10.

[6]Bressi G， Carugno. G， Onofrio. R，et al. Measurement of the Casimir force between parallel metallic surfaces[J]. Physical review letters，2002，88(4):41 804.

[7]沈晓霞.原子与平板间的Casimir-Polder力的基础研究[D].杭州:浙江大学，2013:17-19.

[8]Leonhardt U， Philbin T G. Quantum levitation by left-handed metamaterials[J]. New Journal of Physics，2007，9(8):254.

[9]Rosa F， Dalvit D， Milonni P W. Casimir-Lifshitz theory and metamaterials[J]. Physical review letters，2008，100(18):183 602.

[10]Tse W K， MacDonald A H. Quantized Casimir Force[J]. Physical review letters，2012，109(23):236 806.

The Research on Relative Casimir Force between

the Metamaterials Slabs of Sandwich

Xiao Nan， Zeng Ran， Li Qiliang

(SchoolofCommunicationEngineering，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Key words: relative Casimir force; metamaterials; the amplitude of Casimir force