利用Kloosterman和刻画一类超Bent函数

2016-01-22唐春明亓延峰徐茂智

杭州电子科技大学学报(自然科学版) 2015年1期

唐春明，亓延峰，徐茂智

(1.西华师范大学数学与信息学院，四川南充 637002；2.杭州电子科技大学理学院，浙江杭州 310018;3.北京大学数学科学学院，北京 100871)

摘要：超Bent函数是一类具有特殊性质的Bent函数，在编码、通信和密码学中都有着重要的应用。该文研究一类Dillon型布尔函数，使用指数和给出了此类函数的超Bent性刻画，并建立此类函数的超Bent性与Kloosterman和，三次和之间的联系。在一些特殊情形下，具体考虑此类函数的超Bent性的刻画，使用Kloosterman和以及三次和的一些特殊值来刻画这些函数的超Bent性，并给出了一些具体超Bent函数的例子，方便地给出许多超Bent函数，从而丰富和发展了超Bent函数理论。

关键词：Bent函数；超Bent函数；Dillon型函数；Walsh-Hadamard变换；Kloosterman和

DOI: 10.13954/j.cnki.hdu.2015.01.014

利用Kloosterman和刻画一类超Bent函数

唐春明1，亓延峰2，徐茂智3

(1.西华师范大学数学与信息学院，四川南充 637002；2.杭州电子科技大学理学院，浙江杭州 310018;3.北京大学数学科学学院，北京 100871)

关键词：Bent函数；超Bent函数；Dillon型函数；Walsh-Hadamard变换；Kloosterman和

DOI:10.13954/j.cnki.hdu.2015.01.014

收稿日期：2014-06-06

基金项目：国家自然科学基金资助项目(10990011,11401480,61272499)

作者简介：唐春明(1982-)，男，四川南充人，讲师，密码学与信息安全.

中图分类号：TN918.1

文献标识码：：A

文章编号：：1001-9146(2015)01-0067-08

Abstract:Hyper-Bent functions as a subclass of Bent functions can be applied to coding theory， communication and cryptography. This paper considers a class of Boolean functions with Dillon exponents， characterizes these functions with exponential sums， and presents the link of hyper-Bentness of these hyper-Bent functions with Kloosterman sums and cubic sums. For some special cases， we present the concrete characterization of these hyper-Bent functions with special values of Kloosterman sums and cubic sums， and give some concrete examples of hyper-Bent functions. From our method， many hyper-Bent functions can be given. That enriches the theory of hyper-Bent functions.

0引言

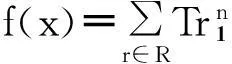
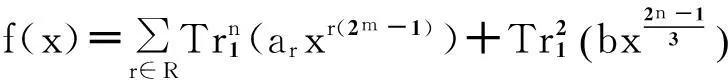
本文第一节给出了一些基本记号，并回顾了bent函数，超bent函数，以及指数和的相关定义和结论。第二节研究一类布尔函数的超bent性，并利用Kloosterman和来刻画此类函数的超Bent性，具体地使用Kloosterman和的特殊值给出了一些此类超bent函数。最后，第三节是全文的一个总结。

1预备知识

1.1　超bent函数

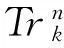
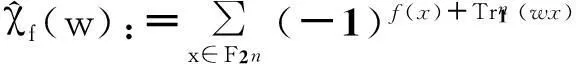
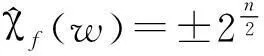
若f是一个Bent函数，那么n必然是一个偶数，而且其代数次数deg(f)≤n/2。超Bent函数是Bent函数中的一个重要的子类，其定义如下。

定义2一个Bent函数称为超Bent函数，若它对满足(i，2n-1)=1的任意i，有f(xi)也是一个Bent函数。

1.2　指数和

下面介绍一些特殊的指数和的定义和结论。

命题1设a∈F2m，则Km(a)∈[-2(m+2)/2+1，2(m+2)/2+1]，而且Km(a)≡0mod 4。

Kloosterman和的如下除法性质也将经常被用到[31]。

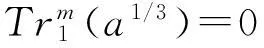
命题3设m是一个奇整数，则：

1)Cm(1，1)=(-1)(m2-1)/82(m+1)/2；

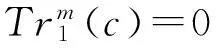
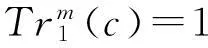
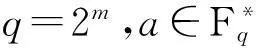
1)Km(a)≡1mod 3；

2)Cm(a，a)=0；

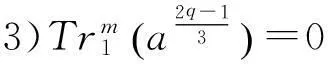
证明由命题2知，结论(1)与(3)等价。

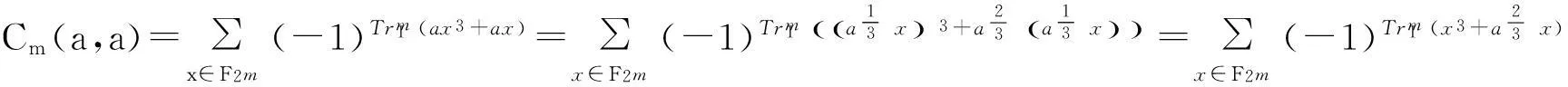
为了记号简单起见，记Cm(a):=Cm(a，a)。将要使用到如下的指数和：

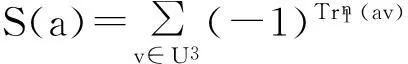
(1)

式中，U3={u3:u∈U}。Mesnager给出了这个指数和与Kloosterman和，三次和之间的关系[16-17]。

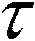
(2)

2超Bent函数和Kloosterman和

考虑如下Dillon型布尔函数：

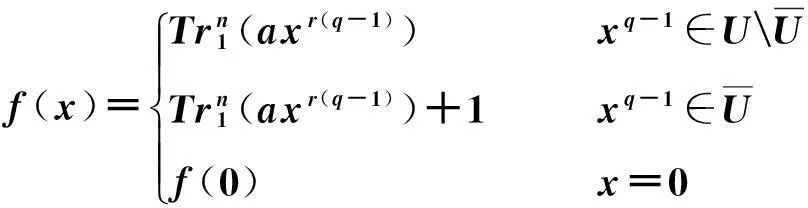
(3)

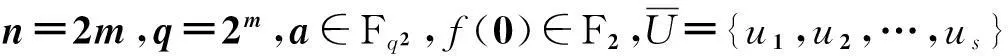
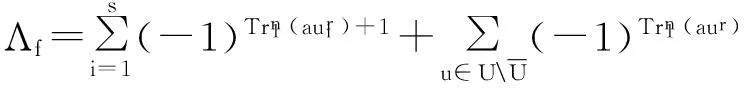
证明使用文献[15，19]中的证明方法考虑f(x)的Walsh-Hadamard谱值，可以得到本引理的结论。

定理1设f(x)如式(3)定义，则：

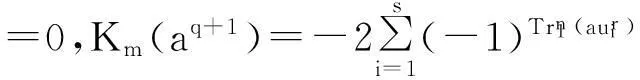
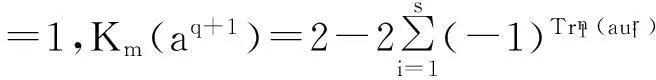
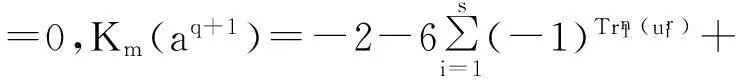
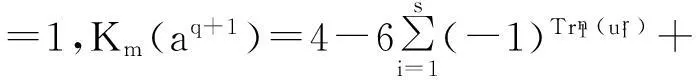
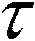
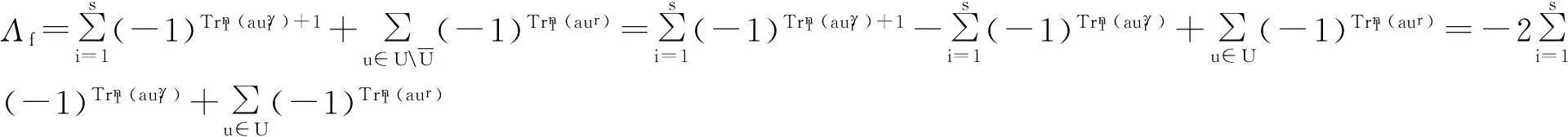
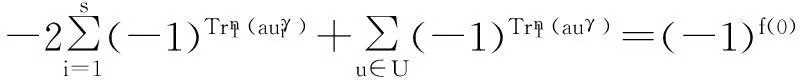
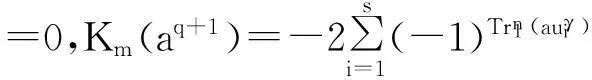
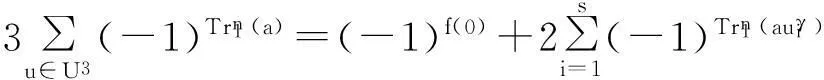
综上，定理得证。

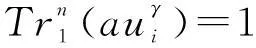
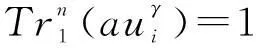
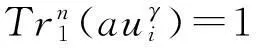
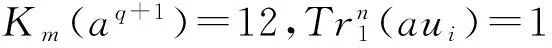
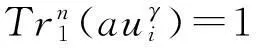
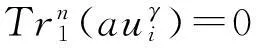
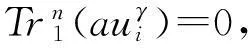
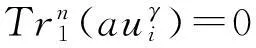
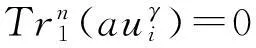
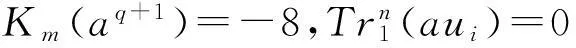
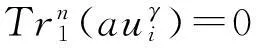
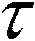
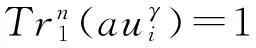
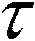
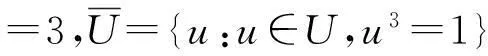
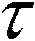
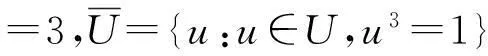
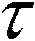
3结束语

参考文献

[1]Rothaus O S. On “bent” functions[J]. Journal of Combinatorial Theory， Series A，1976，20(3):300-305.

[2]Mesnager S. Bent and hyper-bent functions in polynomial form and their link with some exponential sums and Dickson polynomials[J]. Information Theory， IEEE Transactions on，2011，57(9):5 996-6 009.

[3]Carlet C， Gaborit P. Hyper-bent functions and cyclic codes[J]. Journal of Combinatorial Theory， Series A，2006，113(3):466-482.

[4]Carlet C. Boolean functions for cryptography and error correcting codes[J]. Boolean Models and Methods in Mathematics， Computer Science， and Engineering，2010，2:257-397.

[5]Dobbertin H， Leander G. A survey of some recent results on bent functions[M]//Sequences and Their Applications-SETA 2004. Springer Berlin Heidelberg，2005:1-29.

[6]Canteaut A， Charpin P， Kyureghyan G M. A new class of monomial bent functions[J]. Finite Fields and Their Applications，2008，14(1):221-241.

[7]Charpin P， Gong G. Hyperbent functions， Kloosterman sums， and Dickson polynomials[J]. Information Theory， IEEE Transactions on，2008，54(9):4 230-4 238.

[8]Charpin P， Kyureghyan G M. Cubic monomial bent functions: A subclass of M[J]. SIAM Journal on Discrete Mathematics，2008，22(2):650-665.

[9]Dillon J F. Elementary Hadamard difference sets[D]. University of Maryland， College Park.，1974.

[10] Dillon J F， Dobbertin H. New cyclic difference sets with Singer parameters[J]. Finite Fields and Their Applications，2004，10(3):342-389.

[11]Dobbertin H， Leander G， Canteaut A， et al. Construction of bent functions via Niho power functions[J]. Journal of Combinatorial Theory， Series A，2006，113(5):779-798.

[12]Gold R. Maximal recursive sequences with 3-valued recursive cross-correlation functions (Corresp.)[J]. Information Theory， IEEE Transactions on，1968，14(1):154-156.

[13]Leander N G. Monomial bent functions[J]. Information Theory， IEEE Transactions on，2006，52(2):738-743.

[14]Kholosha A， Leander G. Bent Functions With 2^ r Niho Exponents[J]. IEEE Transactions on Information Theory，2006，52(12):5 529-5 532.

[15]Mesnager S. Hyper-bent Boolean functions with multiple trace terms[M]//Arithmetic of Finite Fields. Springer Berlin Heidelberg，2010:97-113.

[16]Mesnager S. A new class of bent and hyper-bent Boolean functions in polynomial forms[J]. Des. Codes Cryptography，2011，59(1-3):265-279.

[17]Mesnager S. A new class of bent Boolean functions in polynomial forms[C] //International Workshop on Coding and Cryptography—WCC 2009. Springer Berlin Heidelberg，2009:5-18.

[18]Mesnager S. A new family of hyper-bent Boolean functions in polynomial form[M]//Cryptography and Coding. Springer Berlin Heidelberg，2009:402-417.

[19]Yu N Y， Gong G. Constructions of quadratic bent functions in polynomial forms[J]. Information Theory， IEEE Transactions on，2006，52(7):3 291-3 299.

[20]Youssef A M， Gong G. Hyper-bent functions[M]. Berlin: Springer Berlin Heidelberg，2001:406-419.

[21]Gong G， Golomb S W. Transform domain analysis of DES[J]. Information Theory， IEEE Transactions on，1999，45(6):2 065-2 073.

[22]Lisonek P. An efficient characterization of a family of hyperbent functions[J]. Information Theory， IEEE Transactions on，2011，57(9):6 010-6 014.

[23]Wang B， Tang C， Qi Y， et al. A New Class of Hyper-bent Boolean Functions with Multiple Trace Terms[J]. IACR Cryptology ePrint Archive，2011，2011:600.

[24]Wang B， Tang C， Qi Y， et al. A generalization of the class of hyper-bent Boolean functions in binomial forms[J]. IACR Cryptology ePrint Archive，2011，2011:698.

[25]Tang C， Qi Y， Xu M， et al. A new class of hyper-bent Boolean functions in binomial forms[J]. arXiv preprint arXiv:1112.0062，2011.

[26]Flori J P， Mesnager S. An efficient characterization of a family of hyper-bent functions with multiple trace terms[J]. Journal of Mathematical Cryptology，2013，7(1):43-68.

[27]Flori J P， Mesnager S. Dickson polynomials， hyperelliptic curves and hyper-bent functions[M]//Sequences and Their Applications-SETA 2012. Springer Berlin Heidelberg，2012:40-52.

[28]Mesnager S， Flori J P. Hyperbent Functions via Dillon-Like Exponents[J]. Information Theory， IEEE Transactions on，2013，59(5):3 215-3 232.

[29]Li N， Helleseth T， Tang X， et al. Several new classes of bent functions from Dillon exponents[J]. IEEE transactions on information theory，2013，59(3):1 818-1 831.

[30]Lachaud G， Wolfmann J. The weights of the orthogonals of the extended quadratic binary Goppa codes[J]. Information Theory， IEEE Transactions on，1990，36(3):686-692.

[31]Charpin P， Helleseth T， Zinoviev V. Divisibility properties of classical binary Kloosterman sums[J]. Discrete Mathematics，2009，309(12):3 975-3 984.

[32]Carlitz L. Explicit evaluation of certain exponential sums[J]. Mathematica Scandinavica，1979，44:5-16.

A Class of Hyper-Bent Functions Characterized by Kloosterman Sums

Tang Chunming1， Qi Yanfeng2， Xu Maozhi3

(1.SchoolofMathematicsandInformation，ChinaWestNormalUniversity，NanchongSichuan637002，China;

2.SchoolofScience，HangzhouDianziUniversity，HangzhouZhejiang310018，China;

3.LMAM，SchoolofMathematicalSciences，PekingUniversity，Beijing100871，China)

Key words: Bent functions; hyper-Bent functions; functions with Dillon exponent; Walsh-Hadmard transform; Kloosterman sums