一种新的混合混沌扩频序列的设计与仿真

2016-01-22张福洪陈妍芬

杭州电子科技大学学报(自然科学版) 2015年1期

邹　凤，张福洪，曾　榕，陈妍芬

(杭州电子科技大学通信工程学院，浙江杭州 310018)

摘要：混沌序列因其码组丰富、抗截获能力强等优点，常作为扩频码。单一混沌映射在平衡特性和随机性等方面存在不足，因而提出了一种新的混合混沌序列。将改进型Logistic映射与Chebyshev映射结合起来组成双混沌系统，在分析这种双混沌序列的相关性能的基础上，将其应用于直接序列扩频系统中。仿真结果表明，新的混合混沌序列具有更好的伪随机特性，能改善系统性能，可代替单一的混沌序列作为扩频码。

关键词：Logistic混沌序列；Chebyshev混沌序列；双混沌序列；直接序列扩频

DOI: 10.13954/j.cnki.hdu.2015.01.011

一种新的混合混沌扩频序列的设计与仿真

邹凤，张福洪，曾榕，陈妍芬

(杭州电子科技大学通信工程学院，浙江杭州 310018)

关键词：Logistic混沌序列；Chebyshev混沌序列；双混沌序列；直接序列扩频

DOI:10.13954/j.cnki.hdu.2015.01.011

收稿日期：2014-05-29

通信作者：

作者简介：邹凤(1988-)，女，四川资阳人，在读研究生，通信系统与信号处理.张福洪副教授，E-mail: fuhong@vip.sina.com.

中图分类号：TN914.42

文献标识码：：A

文章编号：：1001-9146(2015)01-0053-05

Abstract:Because of its rich sequence and good anti-interception capability， chaotic sequence can be used as spreading code. Single chaotic map has disadvantage in the aspects of balance and randomness. To solve this problem， a new hybrid chaotic sequence is proposed. The dual chaotic system is consisted of two chaotic systems which are the improved Logistic map and Chebyshev map. Based on the analysis of relevant properties of this dual chaotic sequence， this sequence will be applied to the direct sequence spread spectrum system. The simulation results show that the new hybrid chaotic sequence， which can be used as spreading code instead of a single chaotic sequence， has better characteristics of pseudo-random and can greatly improve system performance.

0引言

传统的扩频码多采用m序列、Gold序列等伪随机序列[1]，它们具有良好的自相关和互相关性能，但是它们存在数目有限、复杂度低、保密性低、抗截获性低等缺点[2]。因而现阶段多采用混沌序列作为扩频码。混沌系统通过非线性的动力方程构成的，它产生的序列在时域上呈现出随机混乱的状态，具有内随机性、非周期性等特点，其统计特性与白噪声一致，抗干扰能力强，不容易被截获。同时混沌序列具有很强的初值敏感性，当设定的初值有很细微的差别时，通过迭代方程将产生完全不同的混沌序列。因此码组丰富，可用于多址通信系统中。常见的混沌序列有Logistic映射、Tent映射、Chebyshev映射和改进型Logistic映射。文献[3-5]研究了这些单一映射的初值敏感性、非周期性和随机性等相关特性，这些单一映射易于产生和复制，其性能很优良，但单一映射在诸如平衡性和随机性上存在一定的问题，因此本文在文献[6-8]研究的基础上提出了一种新的混沌序列，采用改进型Logistic混沌系统与3阶Chebyshev混沌系统[9]进行组合，构成一个新的双混沌系统。这两种混沌序列均为常见的一维混沌映射，其迭代方程简单，易于实现。

1双混沌系统的设计

1.1　单一映射混沌序列

本文主要研究的混沌序列包括改进型Logistic混沌序列和Chebyshev混沌序列。

Chebyshev混沌序列的为Xn+1=f(Xn)=cos(μcos-1Xn)，Xn∈(-1，1)。

1.2　双混沌序列

假设序列{a1，a2，…，an，…}和{b1,b2,…bn,…}分别为改进型Logistic混沌系统和3阶Chebyshev混沌系统的输出，则有：

(1)

式中，an，bn为当前时刻状态，an+1，bn+1为下一时刻状态。

将这两个系统输出的序列{a1，a2，…，an，…}和{b1,b2,…bn,…}离散量化为二进制序列，然后进行模2相加，形成二进制序列{c1,c2,…cn,…}，这个序列即为双混沌序列。具体离散方法为将混沌系统输出进行如下判决：

(2)

现对双混沌序列的平衡性、相关性和随机特性等方面进行仿真研究。

1.2.1双混沌序列的平衡特性分析

衡量扩频码性能好坏的一个重要标准是平衡度。扩频码序列不平衡会造成频谱的泄露，从而使得传输的信号被发现。因此，必须保证新构建的双混沌系统具有良好的平衡特性，这样才能更加准确的传输信息。

平衡度的定义为：

E=(P-Q)/N

(3)

式中，P为扩频码所包括的‘1’的个数，Q为‘0’的个数，N为扩频码序列长度。

通过仿真得到两种混沌序列随初值变化的平衡度曲线如图1、图2所示。由图1可知改进型Logistic序列和Chebyshev序列在某些初始条件下，其平衡度将会到达较大的值，这为系统带来了非常严重的安全性隐患。

图1　两种单一混沌序列的平衡特性

图2　双混沌序列平衡特性

图2(a)中改进型Logistic混沌系统的初值选取为a0=0.348(不失一般性)，其表示双混沌序列的平衡度随Chebyshev混沌系统初值的变化曲线。由此可见，双混沌序列序列在平衡性方面有很大的改善。图2(b)为双混沌序列平衡度与序列长度的关系曲线，随着序列长度的增加，平衡度趋向平稳。本文均选取长度1 024，此时双混沌序列平衡性良好。

1.2.2双混沌序列的相关性能分析

序列的自相关和互相关特性直接影响着整个系统性能的好坏，选择自相关和互相关性较好的扩频码能够减少系统相互间的干扰，提高信息传输的保密性和可靠性。

图3　几种混沌序列的相关函数

1.2.3双混沌序列的随机特性分析

由美国国家标准技术研究所制定的随机性测试标准包含了16项指标，从不同的方面反应了序列的统计特性。为了更加全面地分析混沌序列的性能，本文选取了其中5项指标，包括频率测试、分组频率测试、游程测试、频谱测试和近似熵测试[10]。测试的方法主要是计算P-value值，并对P-value值进行判决，若P-value值>0.01，则说明测试通过，被检测的序列为随机序列，且序列的P-value值越大，说明序列的随机性能越好。为了使测试的结果更加精确，均舍弃了序列的前1 000个值，表1为Logistic序列、Chebyshev序列和双混沌序列的P-value值记录结果。

在这几种测试中，首先应进行频率测试，如果频率测试不能通过，则不能进行剩下的测试，即频率测试是这几种测试方法的基础。几种混沌序列的随机性测试结果如表1所示，“*”表示未通过测试。由表1可知，在这3种混沌序列中，Chebyshev混沌序列的随机性能最差；初值对于序列的P-value值有一定的影响；适当的增加迭代次数有利于提高双混沌序列的随机性能，但对于Logistic混沌序列的性能没有改善。另外，由Chebyshev序列的测试结果可知，游程测试与近似熵测试这两种测试较难通过。由此可见，双混沌序列有更好的伪随机性能。

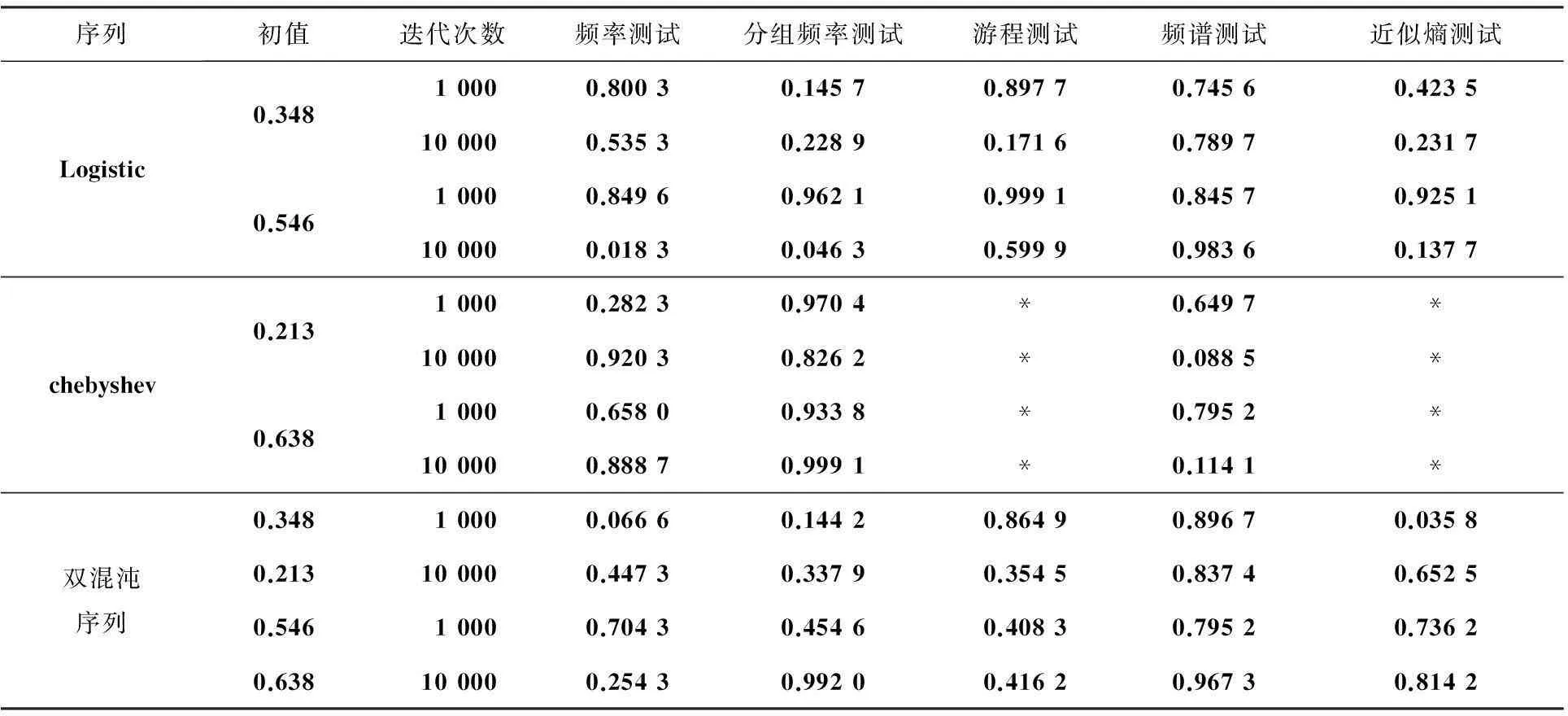
表1　几种混沌序列的随机性测试结果

2系统仿真

图4　直接序列扩频通信系统

图5(a)为混沌序列发生器产生的双混沌序列，由此可知，双混沌序列是由其它两种单一序列异或产生的。对于直扩系统，采用不同的扩频码进行扩频，系统的误码率也有所不同，如图5(b)所示。在Eb/N0=10 dB之前这3种误码率曲线并没有太大的区别，而在之后采用新的双混沌序列作为扩频码的直扩系统的误码率较之其他两种有了较为明显的下降，另外，改进型Logistic混沌序列误码率也低于Chebyshev混沌序列。因此，双混沌序列更适用于扩频通信中。